fibonacci sequence | My Education ePortfolio

My whole life I’ve been musical. My passion started when my mum bought me a harmonica and a second hand keyboard. I fell involve with music and have played an instrument ever since I was 8 years old. I started with the keyboard then progressed to cello, guitar, singing and saxophone. I did grades in saxophone and managed to get to grade 6 by the end of school. I was a key instrument in the school concert band which took me to 2 countries and many concerts around my home. I had a strict pattern of practising every night, much to my mum’s annoyance, and my sister also screeched her clarinet through the house most nights. My musicality and good rhythm combines with my other hobby of dancing, in particular tap which involves precise beats coming from your shoes.

Today in discovering mathematics, Paola talked about the links between maths and music. And not too surprisingly there’s quite a few.

Note values/rhythms
Beats in a bar
Tuning/Pitch
Chords
Counting songs
Fingering on music
Time signature
Figured bass
Scales
Musical Intervals
Fibonacci sequence

“Rhythm depends on arithmetic, harmony draws from basic numerical relationships, and the development of musical themes reflects the world of symmetry and geometry. As Stravinsky once said: “The musician should find in mathematics a study as useful to him as the learning of another language is to a poet. Mathematics swims seductively just below the surface.” (Sautoy, 2011).

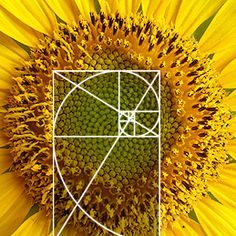
As I have explored in a previous blog, the Fibonacci sequence (the golden ratio) exists in art and nature but did you know it’s also seen within music! If you’ve read my previous blogs you should be all clued up on it. The scales in music relate to the Fibonacci sequence, there are 13 notes in the span of any note within it’s octave. A scale has 8 notes in it, and within that the 3rd and 5th notes, along with the 1st note, create the simple foundations of any given chord. The scale is based on a tone, the tone is a weave of 2 steps and 1 step between notes (black and white) from the root tone (the 1st note of the scale) (Meisner, 2012).

The 5th note is the ruling note of the major scale. This note is also the 8th note of the 13 notes that are in an octave. This gives more proof to the theory of the Fibonacci sequence in music. What’s more, 8 ÷ 13 = 0.61538…, which resembles Phi (Meisner, 2012).

Compositions are frequently based on Phi. The timings in songs reflect the Fibonacci sequence in that when a song climaxes it often lands at 61.8% through the song. We can also find the golden ratio in the design of musical instruments. For example in the violin (Meisner, 2012).

I used to hate doing scales in music lesson. I would always make up rhymes to remember what notes are in which scales. But Paola taught us a mathematical process for know what every note is in every major scale! I wish i’d known this back in school. The pattern goes tone, tone, semitone, tone, tone, tone, semitone. A tone is when you skip a note in-between 2 other notes and a semitone is just one notes to the immediate next note. These all include the black notes (flats and sharps).

The pentatonic scale was a new concept that I hadn’t come across in my previous music knowledge. The scale is found all around the world is every country and is the foundations for a lot of classic hits. The pentatonic scale is made up of 5 key black notes. It has the same pattern as we discussed for the major scales, so a pentatonic C sharpe scale would go C#, D#, F, F#, G#, A#, C, C#.

In closing, interconnectedness is beaming in the subject of music and maths. Liping Ma’s theory is definitely becoming more and more accurate and clear. I can definitely see myself teaching music with connectedness in mind in the future to my classes, which will give them a more thorough understanding of it.

One more thing, did you know it’s impossible to tune a piano!

References:

Du Sautoy, M. (2011). ‘Listen by numbers: music and maths’ Guardian. Available at: http://theclassicalsuite.com/2011/06/listen-by-numbers-music-and-maths-via-guardian (Accessed: 08/11/17).

Meisner, G. (2012). [Website]. Available at: https://www.goldennumber.net/music/ (Accessed 08/11/17)

I came out of this lecture completely mind blown at our world and what is produces naturally, we truly live in an extraordinary reality. Today we learnt about the Fibonacci sequence (the golden spiral) together with Phi (the golden ratio).

In 1509 there was an Italian mathematician called Luna Pacioli who published Divina Proportione, which was a treatise on a number that is known as the ‘Golden Ratio’. We symbolise this ratio by Phi (Φ). This ratio comes with fascinating frequency in nature all around us and mathematics (Pickover, 2009).

The Golden Spiral is made up of the Fibonacci sequence. The sequence is made by the fact that every number after the first two is the sum of the two preceding ones. The Rule is x_n = x_n-1 + x_n-2. The sequence goes:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, … to infinity.

If you draw these numbers out in length x breadth boxes then it creates the golden spiral.

This spiral can be seen in a vast amount of nature from our galaxies to the shell of the nautilus. It is truly mind blowing to say the least, the fractal nature of reality.

A fractal is a way of seeing infinity – Benoît Mandelbrot

The natural world has a fondness of the Fibonacci numbers. If you look at flowers most of them have a Fibonacci number of petals.

3 petals = lily & iris

5 petals= buttercups

8 petals = delphinium

13 petals = marigold & ragwort

21 petals = aster

55/89 petals = daisy

Not all flowers will have these numbers but averagely they do. For instance this is why 4 leaf clovers are so rare as the number 4 is not in the Fibonacci sequence (Bellos, 2010).

Just as pi (π) stands for the ratio of the circumference to the diameter of a circle, Phi (Φ) stands for a special ratio of line segments. When a line is divided in a unique way the ratio Phi happens. “We divide a line into two segments so that the ratio of the whole segment to the longer part is the same as the ratio of the longer part to the shorter part” (Pickover, 2009, p.112).

(a + b)/ b = b/a

The ratio (golden ratio) is 1.61803….

Using this ratio Anna asked us to work in pairs to see how “beautiful” our bodies were. By dividing different measurements by each other we were able to calculate, if our body part = 1.6… then they were “beautiful”. Me and Ellie Kean calculated we both had “beautiful” heights.

The Greeks were amazed by this ‘phi’. They founded the 5-pointed star, it was the admired symbol of the Pythagorean Brotherhood. It was called the ‘extreme and mean ratio’ by Euclid and he was able to make it by a compass and a straightedge method (Bellos, 2010).

Leonardo da Vinci is a prime example of an artist who believed maths and art has a strong bond. This is clearly seen in his most famous drawing of the ‘Vitruvian Man’. The drawing shows mathematically and artistically that the human body is has its perfectly symmetrical measurements and dimensions not by coincidence.

Learn how to see. Realise that everything connects to everything else – Leonardo da Vinci

Overall, there is a true connectedness of mathematics and art. There is proof of this in our worlds nature make-up and has been discovered through history also with the help of Leonardo da Vinci. I can use Leonardo as an inspiration within my future art lessons with students so they can have a more broad understanding of the history of art and how it connects to art we see now in the present day.

References:

Pickover, C. A. (2009) The Math Book From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics. London: Sterling.

Bello, Alex (2010) Alex’s Adventures in Numberland London: Bloomsbury

♪ Do Re Mi Fibonacci ♫

🌻 The Fractal Nature Of Reality 🍀