I came out of this lecture completely mind blown at our world and what is produces naturally, we truly live in an extraordinary reality. Today we learnt about the Fibonacci sequence (the golden spiral) together with Phi (the golden ratio).
In 1509 there was an Italian mathematician called Luna Pacioli who published Divina Proportione, which was a treatise on a number that is known as the ‘Golden Ratio’. We symbolise this ratio by Phi (Φ). This ratio comes with fascinating frequency in nature all around us and mathematics (Pickover, 2009).

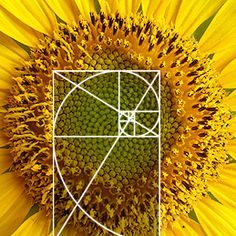
The Golden Spiral is made up of the Fibonacci sequence. The sequence is made by the fact that every number after the first two is the sum of the two preceding ones. The Rule is xn = xn-1 + xn-2. The sequence goes:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, … to infinity.
If you draw these numbers out in length x breadth boxes then it creates the golden spiral.
This spiral can be seen in a vast amount of nature from our galaxies to the shell of the nautilus. It is truly mind blowing to say the least, the fractal nature of reality.



A fractal is a way of seeing infinity – Benoît Mandelbrot
The natural world has a fondness of the Fibonacci numbers. If you look at flowers most of them have a Fibonacci number of petals.
3 petals = lily & iris
5 petals= buttercups
8 petals = delphinium
13 petals = marigold & ragwort
21 petals = aster
55/89 petals = daisy
Not all flowers will have these numbers but averagely they do. For instance this is why 4 leaf clovers are so rare as the number 4 is not in the Fibonacci sequence (Bellos, 2010).
Just as pi (π) stands for the ratio of the circumference to the diameter of a circle, Phi (Φ) stands for a special ratio of line segments. When a line is divided in a unique way the ratio Phi happens. “We divide a line into two segments so that the ratio of the whole segment to the longer part is the same as the ratio of the longer part to the shorter part” (Pickover, 2009, p.112).

(a + b)/ b = b/a
The ratio (golden ratio) is 1.61803….

Using this ratio Anna asked us to work in pairs to see how “beautiful” our bodies were. By dividing different measurements by each other we were able to calculate, if our body part = 1.6… then they were “beautiful”. Me and Ellie Kean calculated we both had “beautiful” heights.
The Greeks were amazed by this ‘phi’. They founded the 5-pointed star, it was the admired symbol of the Pythagorean Brotherhood. It was called the ‘extreme and mean ratio’ by Euclid and he was able to make it by a compass and a straightedge method (Bellos, 2010).
Leonardo da Vinci is a prime example of an artist who believed maths and art has a strong bond. This is clearly seen in his most famous drawing of the ‘Vitruvian Man’. The drawing shows mathematically and artistically that the human body is has its perfectly symmetrical measurements and dimensions not by coincidence.

Learn how to see. Realise that everything connects to everything else – Leonardo da Vinci
Overall, there is a true connectedness of mathematics and art. There is proof of this in our worlds nature make-up and has been discovered through history also with the help of Leonardo da Vinci. I can use Leonardo as an inspiration within my future art lessons with students so they can have a more broad understanding of the history of art and how it connects to art we see now in the present day.
References:
Pickover, C. A. (2009) The Math Book From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics. London: Sterling.
Bello, Alex (2010) Alex’s Adventures in Numberland London: Bloomsbury
