As I write this blog, semester 1 of 2nd year is almost at its end. I get misty-eyed when I think about this model nearly being over as I have enjoyed it so much and learned things I would never have known about otherwise. Truly fascinating module. It’s nothing to do with complex equations or any horrible higher maths recaps. I have mentioned in a serious blog how i didn’t like maths in high school but ‘Discovering Mathematics’ has made me appreciate it again as i now have a deeper and broader understanding of fundamental mathematics and how this links with wider contexts.
Our first ever lecture in this module introduced us to PUFM (profound understanding of fundamental mathematics). At first I just brushed it over as I said to myself I can research into it later on in the module as I didn’t understand it and quite frankly found it confusing.
 Once I came across Liping Ma’s book and read up about her theory then I was able to understand it better and see the links in all my future lectures. Ma wanted to understand why the U.S.A were in a much lower rank for test results than China was. Ma (2010) concluded that the reason the U.S.A were so behind was because teachers didn’t obtain an extensive understanding of elementary mathematics. She figured that during a teachers training they should be made aware and become habitual with basic (fundamental) mathematics as this is what the teachers in China have knowledge on from the start (Ma, 2010).
Once I came across Liping Ma’s book and read up about her theory then I was able to understand it better and see the links in all my future lectures. Ma wanted to understand why the U.S.A were in a much lower rank for test results than China was. Ma (2010) concluded that the reason the U.S.A were so behind was because teachers didn’t obtain an extensive understanding of elementary mathematics. She figured that during a teachers training they should be made aware and become habitual with basic (fundamental) mathematics as this is what the teachers in China have knowledge on from the start (Ma, 2010).
“By profound understanding I mean an understanding of the terrain of fundamental mathematics that is deep, broad and thorough. Although the term ‘profound’ is often considered to mean intellectual depth, it’s three connotations , deep, vast, and thorough, are interconnected.” (Ma, 2010, pp. 120).
To achieve the expected knowledge that Ma thought a teacher should have, she came up with 4 principles that would enable a teacher to have a profound understanding of fundamental mathematics:
Connectedness – “A teacher with PUFM has a general intention to make connections among mathematical concepts and procedures…” (Ma, 2010, pp. 122). This means being able to make links and see connections between mathematical concepts in a wide range of things in society. Also the importance of highlighting this to students when teaching so that they can discover and see these links. In the students learning this would mean that their knowledge learnt would not be fragmented but rather connected.
Multiple Perspectives – “Those who have achieved PUFM appreciate different facets of an idea and various approaches to a solution, as well as their advantages and disadvantages In addition, they are able to provide mathematical explanations of these various facets and approaches…” (Ma, 2010, pp. 122). This means the teacher should respect the multiple aspects of problems and solutions, moving away from there only being one answer. Together with allowing students to inspect these multiple aspects so that they have a flexible understanding of the topic.
Basic Ideas – “Teachers with PUFM display mathematical attitudes and are particularly aware of the “Simple but powerful basic concepts and principles of mathematics” (e.g. the idea of an equation)” (Ma, 2010, pp. 122). This simply means that the teacher should encourage children to explore the points relating to problems. Bringing thoughts back to the basics of mathematics to embolden the students understanding and make the subject less daunting. Students learning and understanding will therefore be more broad and in depth about the subject.
Longitudinal Coherence – “Teachers with PUFM are not limited to the knowledge that should be taught in a certain grade; rather they have achieved a fundamental understanding of the whole elementary mathematics curriculum.” (Ma, 2010, pp. 122). This means that the teacher needs to be able to see where the student is at in their studies and how to progress the student further or fix the problems they are having. The teacher should be of a mind to return and look at learning done in the past, but also able to plan in line with the direction of the classroom’s curriculum and accommodate the students needs within their studies.
“As a mathematics teacher one needs to know the location of each piece of knowledge in the whole mathematical system, its relation with previous knowledge.” (Ma, 2010, pp. 115).
The you look deeper into the 4 principles you can see why mathematics is so important for people to know about. In school, when thinking about the use of connectedness, we need to look across all the curricular areas to see where the links are. This is something a teacher can’t miss out on as mathematics, as I’ve discovered in this module, is in everything that we do in our lives and its important that from an early age we can see how mathematics links with the world around us. When we look into multiple perspectives a myth crops up in my mind that I have heard through out my education, that is that “there is only one process of finding an answer”. This is false. There are many ways in which a problem can be solved, it’s all about teaching the different roots and pathways. The principle of basic ideas is as fundamental to fundamental mathematics as you can get as fundamental is another word for ‘basic’. As professional teachers we need to understand that when teaching young children mathematics, we need to peel back and look deep into the roots so that children progress correctly and will enjoy maths. When we talk about longitudinal coherence, we talk about how we can progress a student further. Teachers need to recognise where a student is at with their learning and identify the correct steps in further educating the student and building on their previous knowledge.
So what have I learned fully for this module? Apart from Liping Ma’s theory about fundamental mathematics, I have learned that mathematics is precisely EVERYWHERE!! Connectedness in full power. I think it is important that when becoming a teacher you need to be aware of this so that you can educate your students on this so they can fully appreciate and enjoy mathematics to the full with the right rooted understanding. Furthermore I am a strong believer in if you’re an enthusiastic teacher while teaching your students will also be enthusiastic about the subjects you teach them. During this module my belief become more true to me as my lecturers were the most enthusiastic mathematics teachers I’d ever seen. This is contagious and made me become even more enthusiastic about the subject myself. Reflecting back on my thought of maths in high school, I’m a changed ‘learner’.
Overall, i think if we suppose a child to have a deep understanding of a specific subject, then so must we.
References:
Ma, L. (2010). Knowing and Teaching Elementary Mathematics: Teachers’ Understanding of Fundamental Mathematics in China and the United States. 2nd ed. New York: Routledge.
 Firstly in the lecture, Richard had us look at an old football score table for 1888-1889 and compare it to the ones we see today. We looked at the rankings, the wins, loses and draws and how many the won for and lost against. To try and make sense of the old table we redesigned it by firstly putting the football team names in order from rank 1-12 and followed that with their point beside them. By ordering the team we used the fundamental mathematics category, from Liping Ma, of basic mathematical principles (Ma, 2010). We used counting to help us order and matching to match up the points form the old table to then new order of teams.
Firstly in the lecture, Richard had us look at an old football score table for 1888-1889 and compare it to the ones we see today. We looked at the rankings, the wins, loses and draws and how many the won for and lost against. To try and make sense of the old table we redesigned it by firstly putting the football team names in order from rank 1-12 and followed that with their point beside them. By ordering the team we used the fundamental mathematics category, from Liping Ma, of basic mathematical principles (Ma, 2010). We used counting to help us order and matching to match up the points form the old table to then new order of teams.




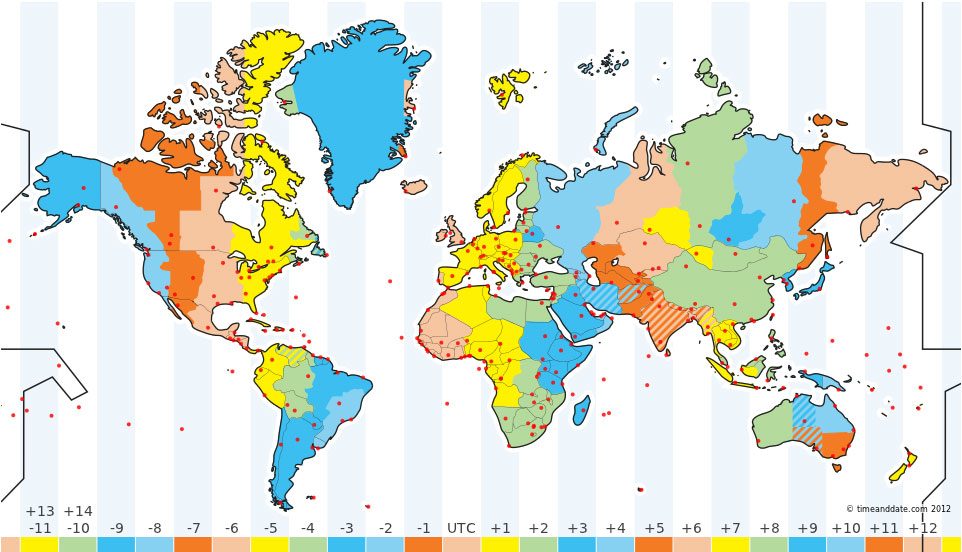
 Horology is the study of time and as humans we base our whole lives around this concept of ‘time’. Our life is a trickling hourglass, and when times up that’s our time up on this earth. We constantly are looking at clocks, updating calendars and setting countless alarms because as humans, many of us are useless as time keeping. It is the core to our daily schedules, without it we would be lost.
Horology is the study of time and as humans we base our whole lives around this concept of ‘time’. Our life is a trickling hourglass, and when times up that’s our time up on this earth. We constantly are looking at clocks, updating calendars and setting countless alarms because as humans, many of us are useless as time keeping. It is the core to our daily schedules, without it we would be lost.