Category Archives: Discovering Maths

Discovering Maths: Going Forward

After receiving our final input today for the Discovering Mathematics module, I realised how much my opinions and misconceptions of mathematics have changed. I wanted to write one final blog post to summarise some of the key discoveries I have made over the course of the semester and the ways in which I will use these discoveries in my teaching practice.

My opinion of mathematics

Before beginning this elective, I was extremely apprehensive about the thought of “doing mathematics”. What I mean by this is that I always viewed mathematics as complicated sums and equations which needed to be solved. I saw mathematics as a stand alone subject because my teachers never made explicit links to the mathematics I was learning and other curricular areas or the wider world. Now, after researching and questioning the mathematics in everyday life – such as in sport, music, art and games – I understand that maths really is everywhere! Even though the links to everyday life and maths may not be explicit, it is evident the importance that basic mathematical principles hold in so many aspects of life. My favourite example of this is the idea of thinking strategically, which is something I have always done when playing a board game for example, but I’ve never considered this to be a mathematical skill.

My favourite discoveries

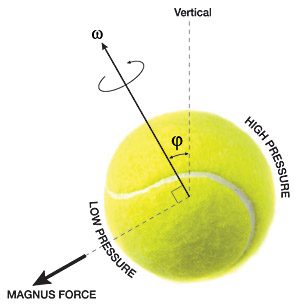
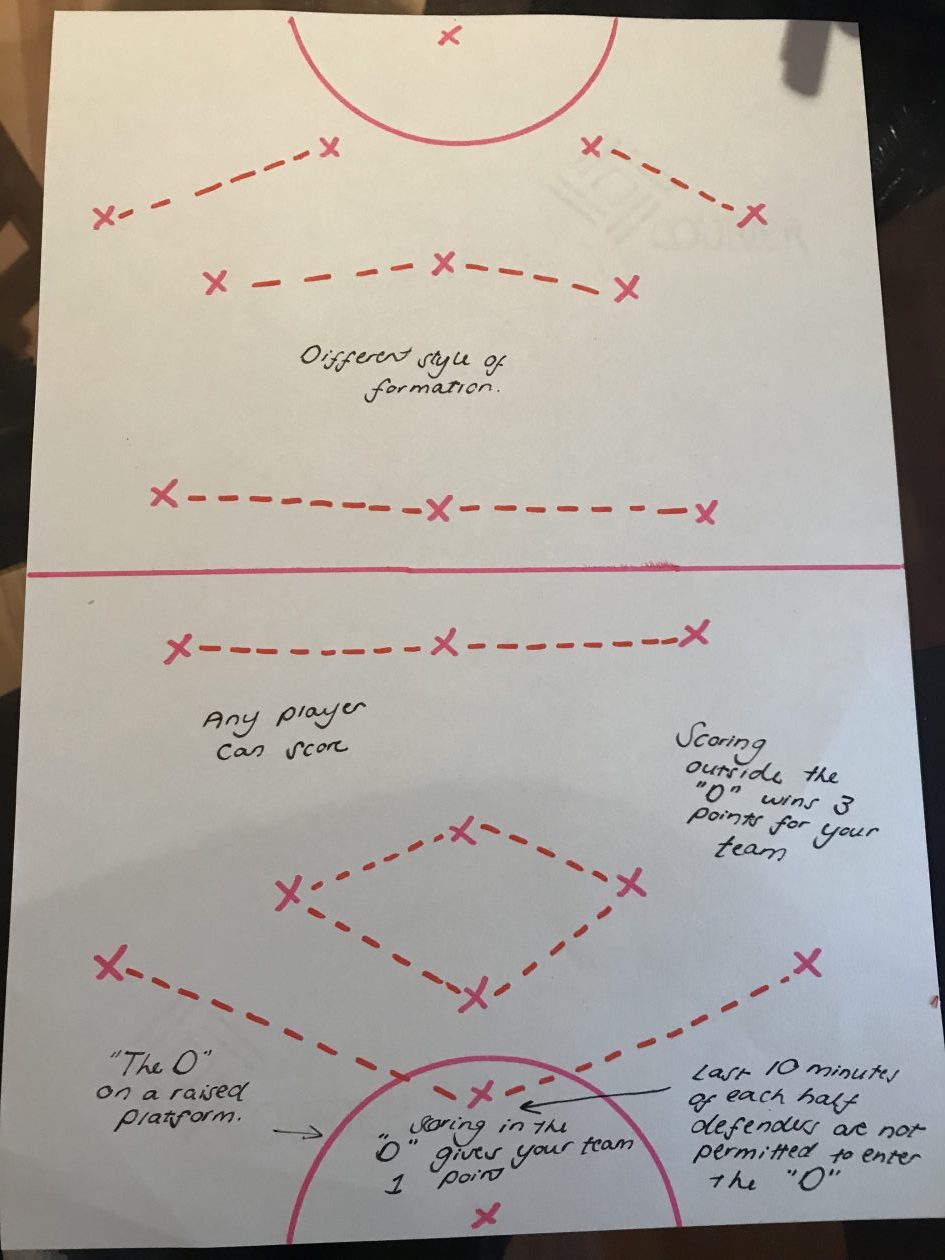
One of my favourite discoveries I made during this module is the link between mathematics and sport. I particularly enjoyed thinking about the mathematics involved in the rules of sport and then reinventing these rules, using the mathematical principles I had identified (Coventry, 2017, a). This is an example of one of the moments when I realised I was really using mathematics rather than simply doing it to solve an equation. I also liked that I could relate mathematics to a dancing – a hobby I’ve enjoyed from an early age. Never did I think I’d be able to relate a passion of mine to a subject I never thought I’d use outside school (Coventry, 2017, b).

How this will influence my teaching practice

Going forward, I am excited to use some of the experiments and examples we have used in class in my own classroom with pupils. In particular I would love them to try and make links to mathematical principles and something they are passionate about such as a sport or a game. This will show the pupils that mathematics is relevant in their lives outside school. I will also be aware of the way I teach mathematics, making sure I issue work which is meaningful and enjoyable for the pupils. A good example I could look at with an upper years class is allowing them to practice their budgeting and money handling skills whilst looking at food chain supply (Sloan, 2017). This would allow pupils to work together in teams to decide what they want to spend their money on, whilst using basic arithmetic to calculate the profit they would make. This is something I feel as though children would become very invested in as they try and beat other groups to make the most money. This could also be a challenge which could be spread across an entire term, with prices for stock changing throughout the duration of the process.

This module has really opened my eyes to the ways in which maths can be explored in wide and meaningful contexts. It has also highlighted the issue that too often people presume they cannot do maths without thinking about what they do in everyday life which is underpinned by mathematical theory and practice. It is therefore vital for me, as a teacher, to make these links explicit to children so they can develop their interest in mathematics throughout their education and beyond.

References

Coventry, J. (2017, a) Discovering Maths in Sport. [Blog] Glow. Available at: https://blogs.glowscotland.org.uk/glowblogs/jceportfolio/2017/11/08/discovering-maths-in-sport/ [Accessed 28 Nov. 2017].

Coventry, J. (2017, b) Discovering Maths in Dance. [Blog] Glow. Available at: https://blogs.glowscotland.org.uk/glowblogs/jceportfolio/2017/09/14/discovering-maths-in-dance/ [Accessed 28 Nov. 2017]

Sloan, A. (2017) The Apprentice Activity. [Blog] Glow. Available at: https://blogs.glowscotland.org.uk/glowblogs/ahseportfolio/2017/11/16/the-apprentice-activity/ [Accessed 28 Nov. 2017]

Mathematics in Computer Games 👾

Leave a reply

As part of this module we have looked at many examples of where fundamental mathematics comes into different industries, one of which being the computer/video game industry.

Image credit: Scratch (2017) https://twitter.com/scratch/

In particular, I wanted to write about mathematics in computer games because when I was younger I was introduced to programmes such as Scratch – a programme which allows you to experiment with computer coding to create your own moving image. When I was learning how to use this programme however, I had no idea that this coding related to mathematics. Even though they are so closely linked – I did not see that computing and mathematics went hand in hand. Just as I was taught procedurally in mathematics it was the same with computing – with no link ever made between the two subjects. Looking back now the connections are clear – understanding numbers to create codes, understanding symbols, patterns and sequences (the list goes on!) But because this wasn’t made explicit, I believed that this type of coding was exclusive to computing and didn’t link to the mathematical concepts I had already learned. This is particularly relevant, considering I was someone who shied away from these topics in mathematics but really enjoyed experimenting and creating codes on Scratch. This also relates to what Ma (1999) explains as “connectedness” – it is important to make the links clear to pupils, not just between mathematic topics, but between maths and other curricular areas, as this makes the learning more relatable for the pupils.

There are many mathematical principles behind the creation of computer games including: geometry, vectors, transformations, matrices and physics (Goodman, 2011). For example, matrices relate to 3D graphics. Many games nowadays take place in a 3D virtual world. Objects and charactrs are created from a set of 3D points. As explained by (Wilkins, n.d., p.3) “these points are stored in a data structure as columns of coordinates relative to a convenient local coordinate system. These objects are manipulated (moved, rotated, scaled) to their desired shap and orientation then positioned in the world by a ‘change of coordinates’ to the world coordinate system”.

Not only is there fundamental mathematics behind the creation of the games but also for playing them. For example, one of the main mathematical skills required to succeed in playing most games is problem solving. In most popular and common games such as, FIFA, Call of Duty and Minecraft there are usually scenarios which require the player to overcome or solve (Tassi, 2016). For example, in FIFA players need to think strategically to work out the best way to tackle other players to get ball possession and the best angle for scoring goals (another mathematical concept!) The creators of these games need to look at the aspect of probability, to ensure players do not encounter the same obstacles all the time or so that they need to defeat these obstacles in different ways.

It is interesting to note that it is stereotypically boys who are deemed to be good at mathematics and science (Coughlan, 2015). Also, it is stereotypically boys who play more computer games (54%) (Takahashi, 2013). Could this therefore prove that video/computer games can enhance mathematical ability? Obviously, this is not a completely accurate argument considering that these are stereotypes, but it does account for the research you find on the two subjects.

As mentioned previously, I never realised the links between mathematics and computing and will therefore ensure that when I am teaching computing in the future I will make the links clear to pupils. Not only this, but hopefully encourage reluctant learners, who struggle with mathematics, that they are able to apply what they know to something fun and creative.

References

Coughlan, S. (2015). Clever girls lack confidence in science and maths. BBC News. [online] Available at: http://www.bbc.co.uk/news/education-31733742 [Accessed 14 Nov. 2017].

Goodman, D. (2011). The Use of Mathematics in Computer Games. NRICH. [online] Available at: https://nrich.maths.org/1374 [Accessed 14 Nov. 2017].

Ma, L. (1999). Knowing and teaching elementary mathematics : teachers’ understanding of fundamental mathematics in China and the United States. Mahwah, N.J.: Lawrence Erlbaum Associates.

Takahashi, D. (2013). More than 1.2 billion people are playing games. VentureBeat. [online] Available at: https://venturebeat.com/2013/11/25/more-than-1-2-billion-people-are-playing-games/ [Accessed 14 Nov. 2017].

Tassi, P. (2016). Here Are The Five Best-Selling Video Games Of All Time. Forbes. [online] Available at: https://www.forbes.com/sites/insertcoin/2016/07/08/here-are-the-five-best-selling-video-games-of-all-time/#7c3b3f025926 [Accessed 14 Nov. 2017].

Wilkins, K. (n.d.). MATHEMATICS FOR COMPUTER GAMES TECHNOLOGY. [ebook] Bathurst. Available at: http://users.math.uoc.gr/~ictm2/Proceedings/pap458.pdf [Accessed 14 Nov. 2017].

Discovering Maths in Sport

Leave a reply

Discovering Maths in Sport

Image credit: Thomas (2012) https://plus.maths.org/content/spinning-perfect-serve

As part of my journey in discovering mathematics, I have become aware of the fact that maths really is everywhere. So far, we have touched on maths in art, stories, music, computing, gambling and sport. In particular I’ve enjoyed looking at these aspects from a very open perspective, questioning the mathematical theory behind the subject. This was especially interesting to look at in relation to sport, where we took a step back from the rules of sport and completely reinvented them.

Firstly, it is important to understand how mathematics relates to sport. There are many specific examples, such as The Magnus effect in tennis which relates to how the ball spins as it moves through the air (Thomas, 2012). A similar example can be seen in badminton where the shuttlecock obeys Newton’s laws of motion. Its acceleration is controlled by the downward force of gravity and a “drag force” from the air that is proportional to the square of the shuttlecock’s speed through the air (The Plus Olympic calendar, 2012).

Although these are very specific examples, we can also see how particular aspects of mathematics relate to nearly all sports: the physics of sport, sporting strategy, architecture and infrastructure, predicting results and sporting statistics, scoring and ranking, and betting and odds (Teacher package: Mathematics in sport, 2010).

Something which we considered during our workshop was whether the popular sports we know well are structured in the best way possible. My group looked at the example of hockey. At first we struggled to come up with ways of improving the sport as we already thought that the rules and strategies of the sport were fair. Then we were posed with the question: what would make hockey more exciting watch? This started to make us think more creatively…

Firstly, we thought about the pitch layout – like most pitches the hockey field is flat. We considered increasing the difficulty of the sport by raising the surface of the area where the goal is (this area is known as the “D” due to its shape – another mathematical link!) If there was a platform of even just a few inches, this would require the players to be able to lift (or chip) the ball and retain control quickly after to avoid defenders “stealing” the ball. One of the key rules for hockey is that you are only allowed to score when you are in the “D”. We thought the game would be more exciting if players were able to score from anywhere on the pitch, meaning that defenders would always need to be alert. We thought we could also change the scoring system so that if players score outside the “D” they can win their team 3 points instead of 1.

Moreover, we thought of a way of motivating players to score more goals. We decided that for the last 10 minutes in each half (hockey is a game of two 35 minutes halves) the defenders would not be allowed to defend inside the “D”. This means that if the player manages to get past the defenders, it is 1v1 scenario with the goal keeper. This would allow the player to show off their scoring skills/abilities.

Below is an illustration of our reinvention of hockey where the crosses represent the players and dashed lines represent their formation:

The ideas that other groups developed also sparked a lot of imagination. I really liked the idea one group came up with in relation to Netball. They imagined what the sport would look like if there were 3 baskets of different heights (each worth different points) instead of just one. Like us, they also looked at the layout of the court but decided to make it larger, to encourage more changeover throughout the match.

This was an extremely engaging workshop which really allowed me to see sport from a different perspective than how I usually would (as very structured and fixed). As we have discovered, mathematics is not always fixed and there are often many ways of doing mathematics. I think this is a lesson I would like to look at in the future as a teacher – to allow the pupils to experiment with sports that they love (see previous blog post about mathematics in dance) (Coventry, 2017). It is also a great way for the children to understand the links and relevance of mathematics.

References

Coventry, J. (2017) Discovering Maths in Dance. [Blog] Glow. Available at: https://blogs.glowscotland.org.uk/glowblogs/jceportfolio/2017/09/14/discovering-maths-in-dance/ [Accessed 8 Nov. 2017].

Teacher package: Mathematics in sport. (2010). Plus. [online] Available at: https://plus.maths.org/content/teacher-package-mathematics-sport [Accessed 8 Nov. 2017].

The Plus Olympic calendar. (2012). Plus. [online] Available at: https://plus.maths.org/content/plus-olympic-calendar-monday-6th-august [Accessed 8 Nov. 2017].

Thomas, R. (2012). Spinning the perfect serve. Plus. [online] Available at: https://plus.maths.org/content/spinning-perfect-serve [Accessed 8 Nov. 2017].

Analogue Clocks: Pointless and Confusing?

Leave a reply

Living in a digital world, I ask the question: do we need to teach pupils how to read an analogue clock in schools?

Although most of us have converted to digital clocks in our online, digital world with our smartphones, computers and televisions; we cannot deny that our encounters with analogue clocks are not completely non-existent. There is an argument that in most places we visit – schools, work offices, supermarkets, restaurants and hotels – we most likely still encounter analogue clocks (Merz, 2014). Therefore, is teaching how to read analogue clocks not a necessary skill to teach pupils in school?

According to Merz (2014), many teachers are frustrated with the idea of this skill being disregarded, with the argument that analogue clocks can provide a vivid representation of time that digital clocks cannot – which can aide visual learners. Analogue clocks can also teach concepts including time management, the passage of time and how much time we have left to complete something (Merz, 2014).

However, with our fast-developing technological advances, it is difficult not to wonder if eventually analogue clocks will disappear in our society. Nowadays, we see plasma screen televisions or digital billboards nearly everywhere we go – displaying digital time. Although analogue clocks are often visually appealing and provide nice décor, they don’t really provide any use other than telling the time. It is therefore arguable that digital screens are much more valuable in society as they are multi-purposeful and allow for more creativity (The benefits of digital billboard advertising, 2015). For example, recently in a shopping centre in Edinburgh, I passed a large television screen which displayed the current top news stories, multiple adverts for new products which could be found in the centre, whilst also displaying the time.

Moreover, one of the key issues with teaching pupils about the analogue clock in schools, is how complex it is for pupils to grasp and understand. This light-hearted, comical video highlights the difficulties for young learners learning how to read time:

https://www.youtube.com/watch?v=0QVPUIRGthI

(Dave Allen – “Teaching Your Kid Time” – ’93 – stereo HQ., 2009)

I partly decided to write this blog post as I was one of the learners in primary school who had difficulties learning about time. I could not wrap my head around the idea of ‘quarter past’, ‘half past’ and ‘quarter to’ (considering we represented every other number on the clock as a number). I also struggled with the concept that there were different ways of reading the clock (e.g. saying 35 past 7 or 25 to 8) which would both be correct. This raises key issues of problem solving and looking at a mathematical concept from multiple perspectives (key skills which are transferrable across all mathematical topics.)

It is important to note that these are aspects of telling the time which apply to both reading the analogue AND digital clock. It is therefore my opinion that the real issue with teaching time to pupils is the concept itself, rather than teaching pupils how to read a particular type of clock. The video above does highlight the difficulties of learning to read an analogue clock – however with the fundamental understanding of the concept of telling the time, I believe that most pupils would welcome the challenge of applying their knowledge to reading an analogue clock. For example, it is vital that children have a strong understanding that 6 is half of 12 to be able to understand why we use the term half past. Another skill which would benefit children before reading an analogue clock is knowing the 5 times table. According to Drabble (2013), without knowing the 5 times table, “anything beyond the o’clocks becomes almost unotainable.” This relates to the idea of longitudinal coherence, introduced by Ma (1999) who states that teachers should use children’s prior knowledge to enhance learning in the topic at hand. It also links with what she writes about basic ideas, meaning that children should revisit the basic concepts they have learned (i.e. fractions and times tables) to understand that they are required for other areas of mathematics (Ma, 1999).

In conclusion, after doing research online and through my own experiences, I believe there is a necessity for teaching pupils about digital and analogue clocks. I believe that we currently live in a world where analogue and digital clocks are both relevant and should therefore both be exposed to pupils. I have realised since studying this issue, that it is important to ensure that pupils understand the principles behind telling the time before introducing them to an analogue OR a digital clock. Furthermore, learning how to read two types of clocks reinforces pupils’ understanding about the concept of time and allows them to practice telling the time from different contexts. This reflects the work of Ma (1999), who highlights the importance of connectedness – meaning that children can link what they have learned to different contexts.

This picture reflects what I saw on my first year placement and shows how to make reading the time on an analogue clock more visually appealing for pupils, whilst also acting as a visual aide (however it is important that pupils realise that they cannot rely on this, as every other analogue clock they see will not be represented in this way!):

Image credit: Teacher’s Pet (2014) www.tpet.co.uk (http://displays.tpet.co.uk/?resource=1507#/ViewResource/id1507)

References

Dave Allen – “Teaching Your Kid Time” – ’93 – stereo HQ. (2009). (Video) YouTube: davidwrightatloppers.

Drabble, E. (2013). How to teach … telling the time. The Guardian. [online] Available at: https://www.theguardian.com/education/teacher-blog/2013/aug/05/telling-the-time-teaching-resources [Accessed 4 Nov. 2017].

Ma, L. (1999). Knowing and teaching elementary mathematics : teachers’ understanding of fundamental mathematics in China and the United States. Mahwah, N.J.: Lawrence Erlbaum Associates.

Merz, S. (2014). Should We Still Teach Analog Clocks?. [Blog] Stories From Schoolaz. Available at: http://www.storiesfromschoolaz.org/still-teach-analog-clocks/ [Accessed 4 Nov. 2017].

The benefits of digital billboard advertising. (2015). [Blog] Signkick. Available at: http://www.signkick.co.uk/blog/the-benefits-of-digital-billboard-advertising/ [Accessed 4 Nov. 2017].

The System

Leave a reply

Following a workshop on the idea of counter-intuitive mathematics, I was intrigued to find out more about how we can look past our intuition or gut feelings to understand mathematical concepts such as probability.

I am someone who struggles to grasp this mathematical concept, as I cannot see past the black and white picture: that everything that happens is completely random and cannot be controlled. To gain a more open mind about this topic I watched the documentary by Derren Brown – The System. This documentary focuses on trying to defy our understanding of probability and to see “the bigger picture”. Derren demonstrates this through inviting people to participate in horse race betting – telling them that he can guarantee they get a win every time.

We follow the journey of Kadesha, who has won every bet since being given anonymous tips from Derren Brown. When Kadesha eventually meets Derren, he explains to her that he has come up with the first “system” which will guarantee her a win for every single horse race she places a bet on. A mathematician worked out the probability of a system being possible to predict the horses accurately and came back with the result 1.48 billion:1 (which is not completely impossible but highly improbable.) So then how can Derren guarantee a win every time?

The truth is, he can’t. What we don’t know as we’re watching Kadesha’s winnings is that there have been 7,775 losses in the process. Altogether, Derren contacted 7,776 random people to take part in this experiment, knowing that someone was bound to win every race. This is because of the extremely high number of people taking part. For each race Derren randomly divided the participants into groups for each horse in the race (so inevitably, one group had to win each round). Kadesha was lucky enough to be part of the winning group every time until the 6^th and final race when she was on her own and Derren could only choose one horse who he thought would win (unlike every other round when he could choose all the horses and at least one person would win their bet.)

This is something which didn’t even occur to me as I was trying to work out how this system was possible. I was honestly convinced Derren was a magician! But now, it makes perfect sense. The system works because Kadesha is not alone. This is exactly the way probability works. The more chances or opportunities you give yourself the more likely you are to be successful.

Derren used a similar example with flipping a coin. He explained that he would flip a coin 10 times and every time it would land on heads. What we don’t realise watching the show is that he had been flipping a coin all day until it came to the point when it landed on heads 10 times in a row – so inevitably it was going to happen eventually.

As stated by Derren: “to work out the system you need to understand that we can only know what comes from our own limited experience and our experience can be very far from the truth.” In my opinion this a great way of explaining counter-intuitive mathematics. If I was someone who had a greater understanding of probability, maybe I could have figured out the hidden secret behind Derren Brown’s “system”. This documentary has also highlighted the importance of looking at concepts from a very open mind (which is something I’ve always struggled with in mathematics and have mentioned in previous blog posts). These are both very important aspects of learning mathematics that I will take forward with me in the future: to look at mathematical concepts from a very open mind and to see how the concepts link with my own experiences or experiences of others.

I have linked below the documentary if you would like to find out if Kadesha won the final race or lost her £4,000 worth of savings… I have also linked an article which explains/criticizes the show.

http://www.independent.co.uk/news/media/sport-on-tv-hes-never-wrong-but-brown-fails-to-frighten-the-bookies-777421.html

References

Derren Brown – The System (Full). (2011). (video) YouTube: ScepticaTV. (https://www.youtube.com/watch?v=9R5OWh7luL4&t=2506s)

Tong, A. (2008). Sport on TV: He’s never wrong but Brown fails to frighten the bookies. The Independent. [online] Available at: http://www.independent.co.uk/news/media/sport-on-tv-hes-never-wrong-but-brown-fails-to-frighten-the-bookies-777421.html [Accessed 30 Oct. 2017].

Do Humans Really Understand Randomness?

Leave a reply

After our input on chance and probability, I was intrigued to investigate the true meaning of randomness and how this relates to our everyday lives.

Randomness in our lives

Randomness is a concept I found very interesting when researching as I never realised how difficult an idea it is for humans to grasp. As humans, we intuitively use our memories to predict what will happen next, whereas true randomness has no memory of what came before (Bellos, 2010). Although we can make educated guesses as to what is to come based on experience and scientific explanation, we really cannot guarantee an outcome for anything.

A funny example of this, as explained by Bellos (2010), is when Apple CEO Steve Jobs had to change the programming behind the ‘shuffle’ feature on iPods. Customers complained that when they used this feature the songs that played were often from the same album or by the same artist. Yet this is extremely possible with randomness, as it does not consider what has already been played. Steve Jobs responded to this feedback by altering the shuffle feature to make it less random, defying the point of randomness altogether!

So why are humans so bad at understanding the concept of randomness?

It is in fact because we have no control over it! As humans, our natural instinct is to give explanations for what happens in our lives – by projecting patterns – and having control in our situations (Bellos, 2010).

I think this relates to the problem humans have when they blame their situations to bad or good luck. Some of us are so invested into the ideas of karma or superstition that we start to lose sight of all the various factors which contribute to our fortunes/misfortunes. Although we might be reluctant to admit it, the random occurrences we encounter come down to chance (Lane, 2011).

An interesting discovery based on luck however, is that “people who believe they are more lucky, are actually likely to be more lucky, because they are more willing to take advantage of opportunities” (Lane, 2011). Furthermore, after carrying out research over several years, Wiseman, (2003) suggests that good luck and bad luck come down to our behaviour and attitudes more than anything else. He explains that lucky people generate good fortune through four basic principles: creating and noticing chance opportunities, listening to their intuitions, having positive expectations, and adopting a resilient attitude (Wiseman, 2003).

It is important to note here that Lane (2011) and Wiseman (2003) suggest that we have control over how we experience a situation rather than have control over the situation itself. For example, someone who considers themselves as lucky may feel lucky about breaking their leg after falling because at least it wasn’t their neck. I think this is where the confusion comes in for humans. We often put a lot of faith in luck, instead of accepting the randomness of events which occur in our lives and facing these events with a positive attitude.

In my opinion, it is not so much the issue that humans do not understand randomness – it’s that we need to accept it! If we accept randomness it is said that we can live a much more carefree and optimistic life (Lane, 2011). It is vital that we teach the concept of probability and chance in school from an early age – not only because it enhances prediction and problem solving skills but so that children can get to grips with this concept and can explore how it relates to their everyday lives (Taylor, n.d.).

Image credit: EX UNO PLURA (2015) (https://www.exunoplura.com/tag/randomness/)

References

Bellos, A. (2010). And now for something completely random. The Daily Mail. [online] Available at: http://www.dailymail.co.uk/home/moslive/article-1334712/Humans-concept-randomness-hard-understand.html [Accessed 16 Oct. 2017].

Lane, M. (2011). Why do we believe in luck?. BBC News: Magazine. [online] Available at: http://www.bbc.co.uk/news/magazine-12934253 [Accessed 16 Oct. 2017].

Taylor, F. (n.d.). Why Teach Probability in the Elementary Classroom?. lamath.org. [online] Available at: http://www.lamath.org/journal/Vol2/taylor.pdf [Accessed 16 Oct. 2017].

Wiseman, R. (2003). Be lucky – it’s an easy skill to learn. The Telegraph. [online] Available at: http://www.telegraph.co.uk/technology/3304496/Be-lucky-its-an-easy-skill-to-learn.html [Accessed 16 Oct. 2017].

Place Value, Number Systems and Their Complexities

1 Reply

Following a workshop this week on the concept of place value, I was inspired to write a blog post on the difficulties and complexities found in these seemingly simple, basic concepts of maths.

As someone who learned mathematics in a procedural fashion, it is very difficult for me to wrap my head around the concepts and understanding behind the maths itself. I therefore found this workshop very challenging when I had to look past the mathematics I have learned and replace it with concepts either made up or used in minority areas across the globe. A good example of this was when we had a look at our number base system…

Understanding place value

Universally the most common number base system is 10 i.e. 1, 2, 3, 4, 5, 6, 7, 8, 9; then using the concept of exchanging or “borrowing” (which is the common term used in schools) to make the number 10 – where the number 1 represents 10 units (Russell, 2017).

I feel like in my experience at school, exchanging (or borrowing as it was called) was never really explained to me. I understood the concept of hundreds, tens and units – but I could never picture that the number 654 could be the same as saying 65 tens and 4 units or that the number 6717 could be the same as saying 67 hundreds and 17 units. To be able to see this and understand it, a key understanding of place value is required.

This was something which I saw as a maths stater activity when I was out on placement. The teacher would ask the children to break down a number and to think of as many ways as possible to express it. This then helped the children as they moved onto their multiplication and division work (where the concept of exchanging is extremely important). I therefore think it is vital that when I go out to teach, I also touch on the theory and concepts behind the topic the children are working on.

It is also vital to use the correct terminology when teaching mathematical concepts like place value. Liping Ma (2010, p.37) explains that 86 percent of Chinese teachers made the change of saying “composing” or “decomposing” a number, rather than using the term “borrowing”. This mathematically makes more sense because when we do a sum like 32 – 15 we need to break the number 32 down to see how we can possibly take the number 5 away from 2. We are not simply “borrowing” but taking 10 units from the tens column. This is something I will take into consideration in my own teaching practice in the future.

Particularly for place value, I have found some great videos online which show how you can teach the concept to children. This is a great example of teaching place value and also using a child’s mistake to create a new learning opportunity:

(Singapore Maths Place Value Lesson, 2015)

The binary system – a great way to visualise place value!

As I feel I was not given the opportunity when I was younger to fully explore the idea of place value, it is difficult for me to see past a 10 base number system when using the concept of place value. In our workshop we were introduced to the most basic system – the binary system. The binary system is a system mainly used for computer systems and technology. A binary number is made up of only 0s and 1s (Mathsisfun.com, 2016). So, the way I explained it to myself, if the highest unit you can have is 1 then the number 2 must be 10, the number three 11, and the number 4 100. This took me a while to grasp as I just couldn’t imagine the hundreds, tens and units columns when working it out in my head. Luckily, we got given a spreadsheet that made the concept much easier to visualise, which was then when I managed to wrap my head around it. I have inserted a similar picture which helps to demonstrate this concept:

Image credit: J.D. Casnig, Knowgramming.com (http://knowgramming.com/nanosemaphore/a_bit_about_binary.htm)

As you can see, the two base system (binary system) is at the bottom. This picture also gives you examples of what it would look like for other number base systems.

10 base system – the best system?

The discussion of a binary system also led to the discussion of a dozenal system. It is argued by many that this makes more mathematical sense than our 10 base number system. Some good examples can be found on the dozenal society website, including: packing/packaging (e.g. we get a dozen eggs), a clock dial is numbered 1-12, and the factors of 12 being more useful than the factors of 10 (Dozenalsociety.org.uk, 2017). This is something which really should get us thinking. I assumed that everything we learn in maths is what makes the most sense but this has highlighted to me the importance of questioning the concepts we learn as there could always be better ways…

So what would a 12 base system look like?

Numbers 1-9 stays the same. The number 10 looks like a rotated 2 and is called dek. The number 11 looks like a rotated 3 and is called el. The number 12 looks like the number 10 and is called doh (Dvorsky, 2013).

An interesting argument for the 10 base system is that it is easier for learners to use their hands to help them count. However, as argued by Dvorsky (2013), we have three separations on each finger, which if used separately would be extremely useful for counting using the dozenal system. If we use our thumb as a pointer, and start with the index finger we can work our way from the bottom of our index finger until we reach the number 12 (or 10) at the top of our pinky. This is difficult to explain without a visualisation so I have attached an illustration below. Using this system, gives us a total of 24 numbers to work with using just our hands!

As noted, there are many complications and arguments for and against a dozenal system that I could write a whole blog post about it. However, I wanted to touch upon it here as something which has inspired me to open my eyes in terms of not seeing mathematics as a set and fixed structure.

Place value and number base systems are both concepts which I have never considered to be so complex until now. Even after doing my research for this blog post and revisiting my notes from the workshop, I am still struggling to pick these concepts apart and look at them from a very open mind. As I develop my thinking throughout this module, I am hoping it will become slightly easier to be able to analyse and question the mathematical concepts I have learned.

References

Casnig, J.D. (2013). A Bit About Binary. [online] Knowgramming.com. Available at: http://knowgramming.com/nanosemaphore/a_bit_about_binary.htm [Accessed 4 Oct. 2017].

Dozenalsociety.org.uk. (2017). DSGB. [online] Available at: http://www.dozenalsociety.org.uk/ [Accessed 6 Oct. 2017].

Ma, L., (2010) Knowing and teaching elementary mathematics (Anniversary Ed.)New York: Routledge.

Mathsisfun.com. (2016). Binary Number System. [online] Available at: https://www.mathsisfun.com/binary-number-system.html [Accessed 4 Oct. 2017].

Russell, D. (2017). Basic Math Concepts: What Is Place Value?. [online] ThoughtCo. Available at: https://www.thoughtco.com/understanding-place-value-2312089 [Accessed 4 Oct. 2017].

Singapore Maths Place Value Lesson. (2015) (video) YouTube: Singapore Maths Academy (UK).

Stand and Deliver

Leave a reply

As part of our introduction to this module it was recommended that we watch the film Stand and Deliver and to analyse the character of Jaime Escalante – a maths teacher at Garfield High School, East Los Angeles, California. We had one question to answer:

Why is Jaime Escalante Different?

Jaime is different because he takes into account each and every pupil in his class; not only their ability but their individual personalities and lives beyond the classroom. His relationship with the pupils is what encourages the pupils to work with him, rather than see him like all their other teachers (who see them as nothing more than pupils in a classroom.) I believe the class gel so well together by the end of the film because Jaime uses each of their strengths to solve problems together as class, rather than only helping those in the class who seem the most interested and able. Jaime also teaches the pupils fundamental problem solving skills before teaching them anything difficult which provides the pupils with the foundation they need in order to go onto advanced calculus. On the other hand, a lot of the time teachers focus on the topic at hand and not the skills which are needed in order to make the topic manageable for pupils. Jaime also regularly relates what he is teaching to real-life concepts which makes the classes more relatable for the pupils. He doesn’t shy away from taboo subjects, such as sex, but instead uses these to facilitate learning.

This is a great film which really highlights the importance of the difference a teacher can make when it comes to teaching topics like maths, which a lot of students shy away from. It also shows that bringing your own enthusiasm and confidence to a classroom can encourage other pupils, who have previously had a bad relationship with maths or school, that they can do well and succeed. These are all key attributes that I will ensure I bring forward with me when teaching mathematics in the future…

Image credit: http://www.ranker.com/list/stand-and-deliver-characters/reference

Discovering Maths in Dance

Leave a reply

I have to admit, I am always one of the people who raise their hands when the question is asked: “Who here has an anxiety when it comes to Maths?” I still vividly remember receiving results from a maths test in primary 7 and thinking that this was it – me and maths weren’t compatible. To be honest with myself I know I’m not hopeless at maths. I understand basic concepts and I am able to apply them – it is problem solving that stumps me. So why do I then look back on my entire school experience of maths as terrible, frightening and impossible?

Because like most other human beings I dwell on the things I can’t do, rather than take time to think about all the things I can. This is why I am most looking forward to rediscovering my misconceptions and anxieties of maths throughout this module. I have already started to consider maths in contexts outside of school, such as where maths fits into my daily life.

A good example is at dancing. Growing up, I went to dancing to switch off from school, but since starting this module I now realise how the dancing I did linked so closely with mathematical concepts I had learned.

Shape

Shape refers to various features in dance. It can refer to the shape of the room or stage you are dancing on. It may also refer to your movements. Usually my dance teachers would try to compare movements to shapes in order to help us picture how our movements should look to the audience. A good example of this is a ‘plie’ in ballet. My dance teacher would always tell us to imagine we were making diamond shape with our legs.

Photo Credit: Kryssia Campos | Getty Images (cited in The Rockettes, 2017)

Shape is also significant in a group dance. Usually the choreographer needs to consider positioning so that everyone can be seen from the audience and to make the dance look more attractive.

Space

“Spatial awareness is an organised knowledge of objects including oneself, in a given space. Spatial awareness also involves understanding the relationships of these objects when there is a change of position. Obviously this is complex mental skill, one that children must hone from a young age.” (Morrisey, 2016)

As a dancer, you must make good use of the space around you. I remember as a young dancer my teacher would make me put my arms out to the side to make a T shape with my body and spin around in circles to make sure I couldn’t touch anyone. Of course, by the time I was older they expected me to have a bit more spatial awareness but this is a concept which was developed from a very early age. Spatial awareness in dancing refers to being aware of the dancers around you and also the size and shape of the room to ensure you are making appropriate use of the space you have.

Time

Timing is an extremely important aspect of dancing as you must be able to count beats and recognise rhythms. Most specifically the examinations in the classical styles of dancing, including tap, jazz and ballet, include timing as one of the specific criteria. This is a table taken from the Royal Academy of Dance specifications for Grade 1, which shows that even from the earliest of grades they expect pupils to understand the concept of sequences and timing (sequencing being another important mathematical concept.)

(Royal Academy of Dance: Specification, 2017)

Terminology & Sequences

Even the terminology used in dance and maths is linked. For example, in ballet there are terms used to describe which position you should be in which include ‘first position’, ‘second position’ and ‘third position’. This uses the basic concepts of number sequences and counting which is one of the first mathematical concepts you are introduced to in school.

These are all concepts that I knew were important in maths and dancing separately, but it has taken me until now to realise how closely they link together. Obviously there are many more concepts I haven’t even touched on, like position and movement, but that shows how many mathematical concepts there are and how relevant they are in day-to-day life. I think this will be a post that as I go through the module I can reflect back on and probably make even more links between maths and my everyday life. I think looking at sports in particular is a great way to make links with mathematical concepts you have learned and you’ll be surprised at how many you can relate to!

References

How to Do the 5 Basic Positions | Ballet Dance. (2011). (Video) YouTube: HowcastArtsRec.

Morrisey, B. (2016). Spatial Awareness in Young Children. [online] Kidsdevelopment.co.uk. Available at: http://www.kidsdevelopment.co.uk/spatialawarenessyoungchildren.html [Accessed 14 Sep. 2017]

Royal Academy of Dance: Specification (2017). [ebook] London: Royal Academy of Dance Enterprises Ltd, p.7. Available at: https://www.rad.org.uk/achieve/exams/what-we-do/rules-regulations-and-specifications [Accessed 14 Sep. 2017].

The Rockettes. (2017). Ballet 101: How to Do a Plié. [online] Available at: https://www.rockettes.com/blog/ballet-101-how-to-do-a-plie/ [Accessed 14 Sep. 2017].