Tag Archives: maths

Do Humans Really Understand Randomness?

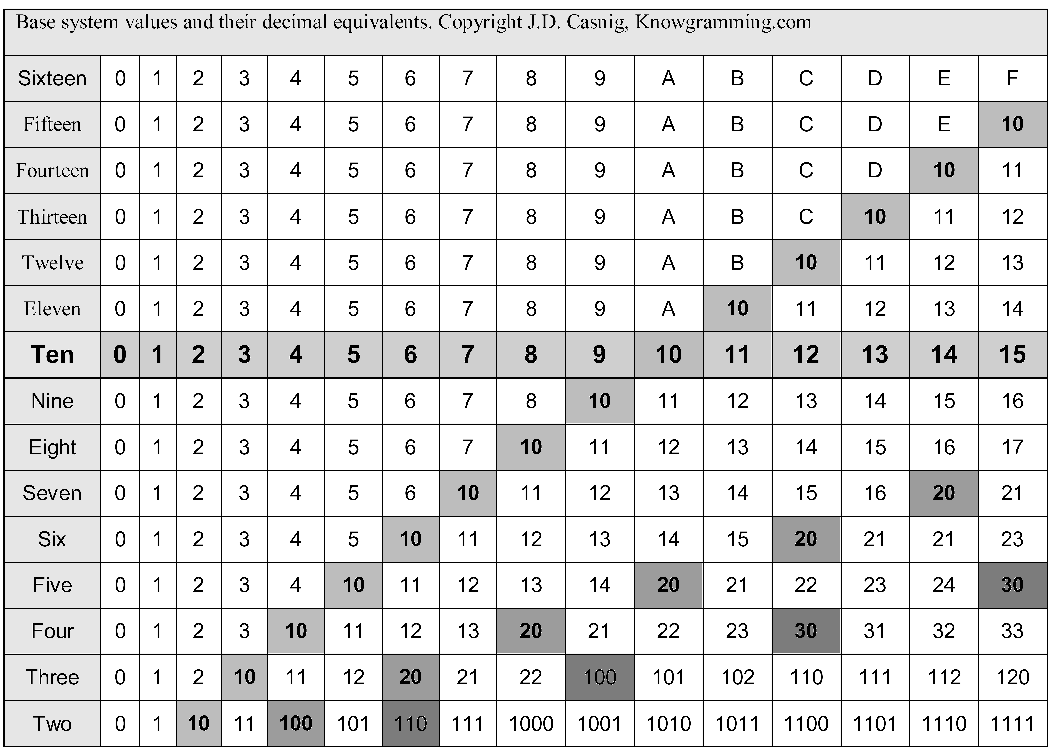
After our input on chance and probability, I was intrigued to investigate the true meaning of randomness and how this relates to our everyday lives.

Randomness in our lives

Randomness is a concept I found very interesting when researching as I never realised how difficult an idea it is for humans to grasp. As humans, we intuitively use our memories to predict what will happen next, whereas true randomness has no memory of what came before (Bellos, 2010). Although we can make educated guesses as to what is to come based on experience and scientific explanation, we really cannot guarantee an outcome for anything.

A funny example of this, as explained by Bellos (2010), is when Apple CEO Steve Jobs had to change the programming behind the ‘shuffle’ feature on iPods. Customers complained that when they used this feature the songs that played were often from the same album or by the same artist. Yet this is extremely possible with randomness, as it does not consider what has already been played. Steve Jobs responded to this feedback by altering the shuffle feature to make it less random, defying the point of randomness altogether!

So why are humans so bad at understanding the concept of randomness?

It is in fact because we have no control over it! As humans, our natural instinct is to give explanations for what happens in our lives – by projecting patterns – and having control in our situations (Bellos, 2010).

I think this relates to the problem humans have when they blame their situations to bad or good luck. Some of us are so invested into the ideas of karma or superstition that we start to lose sight of all the various factors which contribute to our fortunes/misfortunes. Although we might be reluctant to admit it, the random occurrences we encounter come down to chance (Lane, 2011).

An interesting discovery based on luck however, is that “people who believe they are more lucky, are actually likely to be more lucky, because they are more willing to take advantage of opportunities” (Lane, 2011). Furthermore, after carrying out research over several years, Wiseman, (2003) suggests that good luck and bad luck come down to our behaviour and attitudes more than anything else. He explains that lucky people generate good fortune through four basic principles: creating and noticing chance opportunities, listening to their intuitions, having positive expectations, and adopting a resilient attitude (Wiseman, 2003).

It is important to note here that Lane (2011) and Wiseman (2003) suggest that we have control over how we experience a situation rather than have control over the situation itself. For example, someone who considers themselves as lucky may feel lucky about breaking their leg after falling because at least it wasn’t their neck. I think this is where the confusion comes in for humans. We often put a lot of faith in luck, instead of accepting the randomness of events which occur in our lives and facing these events with a positive attitude.

In my opinion, it is not so much the issue that humans do not understand randomness – it’s that we need to accept it! If we accept randomness it is said that we can live a much more carefree and optimistic life (Lane, 2011). It is vital that we teach the concept of probability and chance in school from an early age – not only because it enhances prediction and problem solving skills but so that children can get to grips with this concept and can explore how it relates to their everyday lives (Taylor, n.d.).

Image credit: EX UNO PLURA (2015) (https://www.exunoplura.com/tag/randomness/)

References

Bellos, A. (2010). And now for something completely random. The Daily Mail. [online] Available at: http://www.dailymail.co.uk/home/moslive/article-1334712/Humans-concept-randomness-hard-understand.html [Accessed 16 Oct. 2017].

Lane, M. (2011). Why do we believe in luck?. BBC News: Magazine. [online] Available at: http://www.bbc.co.uk/news/magazine-12934253 [Accessed 16 Oct. 2017].

Taylor, F. (n.d.). Why Teach Probability in the Elementary Classroom?. lamath.org. [online] Available at: http://www.lamath.org/journal/Vol2/taylor.pdf [Accessed 16 Oct. 2017].

Wiseman, R. (2003). Be lucky – it’s an easy skill to learn. The Telegraph. [online] Available at: http://www.telegraph.co.uk/technology/3304496/Be-lucky-its-an-easy-skill-to-learn.html [Accessed 16 Oct. 2017].

Place Value, Number Systems and Their Complexities

1 Reply

Following a workshop this week on the concept of place value, I was inspired to write a blog post on the difficulties and complexities found in these seemingly simple, basic concepts of maths.

As someone who learned mathematics in a procedural fashion, it is very difficult for me to wrap my head around the concepts and understanding behind the maths itself. I therefore found this workshop very challenging when I had to look past the mathematics I have learned and replace it with concepts either made up or used in minority areas across the globe. A good example of this was when we had a look at our number base system…

Understanding place value

Universally the most common number base system is 10 i.e. 1, 2, 3, 4, 5, 6, 7, 8, 9; then using the concept of exchanging or “borrowing” (which is the common term used in schools) to make the number 10 – where the number 1 represents 10 units (Russell, 2017).

I feel like in my experience at school, exchanging (or borrowing as it was called) was never really explained to me. I understood the concept of hundreds, tens and units – but I could never picture that the number 654 could be the same as saying 65 tens and 4 units or that the number 6717 could be the same as saying 67 hundreds and 17 units. To be able to see this and understand it, a key understanding of place value is required.

This was something which I saw as a maths stater activity when I was out on placement. The teacher would ask the children to break down a number and to think of as many ways as possible to express it. This then helped the children as they moved onto their multiplication and division work (where the concept of exchanging is extremely important). I therefore think it is vital that when I go out to teach, I also touch on the theory and concepts behind the topic the children are working on.

It is also vital to use the correct terminology when teaching mathematical concepts like place value. Liping Ma (2010, p.37) explains that 86 percent of Chinese teachers made the change of saying “composing” or “decomposing” a number, rather than using the term “borrowing”. This mathematically makes more sense because when we do a sum like 32 – 15 we need to break the number 32 down to see how we can possibly take the number 5 away from 2. We are not simply “borrowing” but taking 10 units from the tens column. This is something I will take into consideration in my own teaching practice in the future.

Particularly for place value, I have found some great videos online which show how you can teach the concept to children. This is a great example of teaching place value and also using a child’s mistake to create a new learning opportunity:

(Singapore Maths Place Value Lesson, 2015)

The binary system – a great way to visualise place value!

As I feel I was not given the opportunity when I was younger to fully explore the idea of place value, it is difficult for me to see past a 10 base number system when using the concept of place value. In our workshop we were introduced to the most basic system – the binary system. The binary system is a system mainly used for computer systems and technology. A binary number is made up of only 0s and 1s (Mathsisfun.com, 2016). So, the way I explained it to myself, if the highest unit you can have is 1 then the number 2 must be 10, the number three 11, and the number 4 100. This took me a while to grasp as I just couldn’t imagine the hundreds, tens and units columns when working it out in my head. Luckily, we got given a spreadsheet that made the concept much easier to visualise, which was then when I managed to wrap my head around it. I have inserted a similar picture which helps to demonstrate this concept:

Image credit: J.D. Casnig, Knowgramming.com (http://knowgramming.com/nanosemaphore/a_bit_about_binary.htm)

As you can see, the two base system (binary system) is at the bottom. This picture also gives you examples of what it would look like for other number base systems.

10 base system – the best system?

The discussion of a binary system also led to the discussion of a dozenal system. It is argued by many that this makes more mathematical sense than our 10 base number system. Some good examples can be found on the dozenal society website, including: packing/packaging (e.g. we get a dozen eggs), a clock dial is numbered 1-12, and the factors of 12 being more useful than the factors of 10 (Dozenalsociety.org.uk, 2017). This is something which really should get us thinking. I assumed that everything we learn in maths is what makes the most sense but this has highlighted to me the importance of questioning the concepts we learn as there could always be better ways…

So what would a 12 base system look like?

Numbers 1-9 stays the same. The number 10 looks like a rotated 2 and is called dek. The number 11 looks like a rotated 3 and is called el. The number 12 looks like the number 10 and is called doh (Dvorsky, 2013).

An interesting argument for the 10 base system is that it is easier for learners to use their hands to help them count. However, as argued by Dvorsky (2013), we have three separations on each finger, which if used separately would be extremely useful for counting using the dozenal system. If we use our thumb as a pointer, and start with the index finger we can work our way from the bottom of our index finger until we reach the number 12 (or 10) at the top of our pinky. This is difficult to explain without a visualisation so I have attached an illustration below. Using this system, gives us a total of 24 numbers to work with using just our hands!

As noted, there are many complications and arguments for and against a dozenal system that I could write a whole blog post about it. However, I wanted to touch upon it here as something which has inspired me to open my eyes in terms of not seeing mathematics as a set and fixed structure.

Place value and number base systems are both concepts which I have never considered to be so complex until now. Even after doing my research for this blog post and revisiting my notes from the workshop, I am still struggling to pick these concepts apart and look at them from a very open mind. As I develop my thinking throughout this module, I am hoping it will become slightly easier to be able to analyse and question the mathematical concepts I have learned.

References

Casnig, J.D. (2013). A Bit About Binary. [online] Knowgramming.com. Available at: http://knowgramming.com/nanosemaphore/a_bit_about_binary.htm [Accessed 4 Oct. 2017].

Dozenalsociety.org.uk. (2017). DSGB. [online] Available at: http://www.dozenalsociety.org.uk/ [Accessed 6 Oct. 2017].

Ma, L., (2010) Knowing and teaching elementary mathematics (Anniversary Ed.)New York: Routledge.

Mathsisfun.com. (2016). Binary Number System. [online] Available at: https://www.mathsisfun.com/binary-number-system.html [Accessed 4 Oct. 2017].

Russell, D. (2017). Basic Math Concepts: What Is Place Value?. [online] ThoughtCo. Available at: https://www.thoughtco.com/understanding-place-value-2312089 [Accessed 4 Oct. 2017].

Singapore Maths Place Value Lesson. (2015) (video) YouTube: Singapore Maths Academy (UK).

Discovering Maths in Dance

Leave a reply

I have to admit, I am always one of the people who raise their hands when the question is asked: “Who here has an anxiety when it comes to Maths?” I still vividly remember receiving results from a maths test in primary 7 and thinking that this was it – me and maths weren’t compatible. To be honest with myself I know I’m not hopeless at maths. I understand basic concepts and I am able to apply them – it is problem solving that stumps me. So why do I then look back on my entire school experience of maths as terrible, frightening and impossible?

Because like most other human beings I dwell on the things I can’t do, rather than take time to think about all the things I can. This is why I am most looking forward to rediscovering my misconceptions and anxieties of maths throughout this module. I have already started to consider maths in contexts outside of school, such as where maths fits into my daily life.

A good example is at dancing. Growing up, I went to dancing to switch off from school, but since starting this module I now realise how the dancing I did linked so closely with mathematical concepts I had learned.

Shape

Shape refers to various features in dance. It can refer to the shape of the room or stage you are dancing on. It may also refer to your movements. Usually my dance teachers would try to compare movements to shapes in order to help us picture how our movements should look to the audience. A good example of this is a ‘plie’ in ballet. My dance teacher would always tell us to imagine we were making diamond shape with our legs.

Photo Credit: Kryssia Campos | Getty Images (cited in The Rockettes, 2017)

Shape is also significant in a group dance. Usually the choreographer needs to consider positioning so that everyone can be seen from the audience and to make the dance look more attractive.

Space

“Spatial awareness is an organised knowledge of objects including oneself, in a given space. Spatial awareness also involves understanding the relationships of these objects when there is a change of position. Obviously this is complex mental skill, one that children must hone from a young age.” (Morrisey, 2016)

As a dancer, you must make good use of the space around you. I remember as a young dancer my teacher would make me put my arms out to the side to make a T shape with my body and spin around in circles to make sure I couldn’t touch anyone. Of course, by the time I was older they expected me to have a bit more spatial awareness but this is a concept which was developed from a very early age. Spatial awareness in dancing refers to being aware of the dancers around you and also the size and shape of the room to ensure you are making appropriate use of the space you have.

Time

Timing is an extremely important aspect of dancing as you must be able to count beats and recognise rhythms. Most specifically the examinations in the classical styles of dancing, including tap, jazz and ballet, include timing as one of the specific criteria. This is a table taken from the Royal Academy of Dance specifications for Grade 1, which shows that even from the earliest of grades they expect pupils to understand the concept of sequences and timing (sequencing being another important mathematical concept.)

(Royal Academy of Dance: Specification, 2017)

Terminology & Sequences

Even the terminology used in dance and maths is linked. For example, in ballet there are terms used to describe which position you should be in which include ‘first position’, ‘second position’ and ‘third position’. This uses the basic concepts of number sequences and counting which is one of the first mathematical concepts you are introduced to in school.

These are all concepts that I knew were important in maths and dancing separately, but it has taken me until now to realise how closely they link together. Obviously there are many more concepts I haven’t even touched on, like position and movement, but that shows how many mathematical concepts there are and how relevant they are in day-to-day life. I think this will be a post that as I go through the module I can reflect back on and probably make even more links between maths and my everyday life. I think looking at sports in particular is a great way to make links with mathematical concepts you have learned and you’ll be surprised at how many you can relate to!

References

How to Do the 5 Basic Positions | Ballet Dance. (2011). (Video) YouTube: HowcastArtsRec.

Morrisey, B. (2016). Spatial Awareness in Young Children. [online] Kidsdevelopment.co.uk. Available at: http://www.kidsdevelopment.co.uk/spatialawarenessyoungchildren.html [Accessed 14 Sep. 2017]

Royal Academy of Dance: Specification (2017). [ebook] London: Royal Academy of Dance Enterprises Ltd, p.7. Available at: https://www.rad.org.uk/achieve/exams/what-we-do/rules-regulations-and-specifications [Accessed 14 Sep. 2017].

The Rockettes. (2017). Ballet 101: How to Do a Plié. [online] Available at: https://www.rockettes.com/blog/ballet-101-how-to-do-a-plie/ [Accessed 14 Sep. 2017].