2.1 Curriculum |

Discovering Maths in Sport

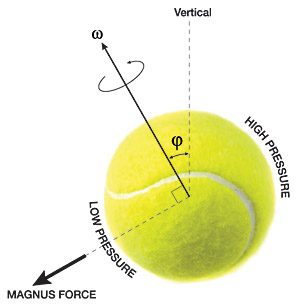
Image credit: Thomas (2012) https://plus.maths.org/content/spinning-perfect-serve

As part of my journey in discovering mathematics, I have become aware of the fact that maths really is everywhere. So far, we have touched on maths in art, stories, music, computing, gambling and sport. In particular I’ve enjoyed looking at these aspects from a very open perspective, questioning the mathematical theory behind the subject. This was especially interesting to look at in relation to sport, where we took a step back from the rules of sport and completely reinvented them.

Firstly, it is important to understand how mathematics relates to sport. There are many specific examples, such as The Magnus effect in tennis which relates to how the ball spins as it moves through the air (Thomas, 2012). A similar example can be seen in badminton where the shuttlecock obeys Newton’s laws of motion. Its acceleration is controlled by the downward force of gravity and a “drag force” from the air that is proportional to the square of the shuttlecock’s speed through the air (The Plus Olympic calendar, 2012).

Although these are very specific examples, we can also see how particular aspects of mathematics relate to nearly all sports: the physics of sport, sporting strategy, architecture and infrastructure, predicting results and sporting statistics, scoring and ranking, and betting and odds (Teacher package: Mathematics in sport, 2010).

Something which we considered during our workshop was whether the popular sports we know well are structured in the best way possible. My group looked at the example of hockey. At first we struggled to come up with ways of improving the sport as we already thought that the rules and strategies of the sport were fair. Then we were posed with the question: what would make hockey more exciting watch? This started to make us think more creatively…

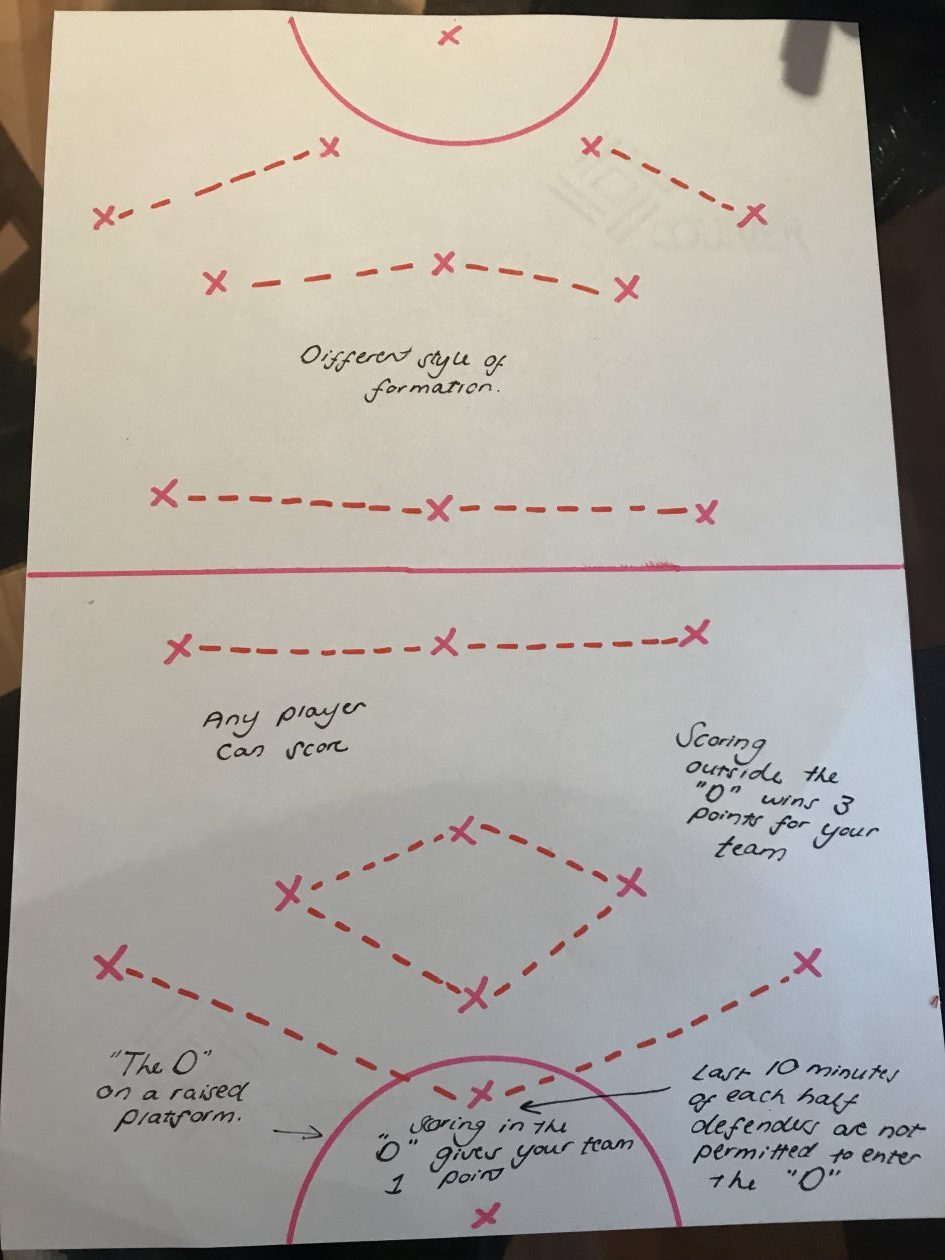
Firstly, we thought about the pitch layout – like most pitches the hockey field is flat. We considered increasing the difficulty of the sport by raising the surface of the area where the goal is (this area is known as the “D” due to its shape – another mathematical link!) If there was a platform of even just a few inches, this would require the players to be able to lift (or chip) the ball and retain control quickly after to avoid defenders “stealing” the ball. One of the key rules for hockey is that you are only allowed to score when you are in the “D”. We thought the game would be more exciting if players were able to score from anywhere on the pitch, meaning that defenders would always need to be alert. We thought we could also change the scoring system so that if players score outside the “D” they can win their team 3 points instead of 1.

Moreover, we thought of a way of motivating players to score more goals. We decided that for the last 10 minutes in each half (hockey is a game of two 35 minutes halves) the defenders would not be allowed to defend inside the “D”. This means that if the player manages to get past the defenders, it is 1v1 scenario with the goal keeper. This would allow the player to show off their scoring skills/abilities.

Below is an illustration of our reinvention of hockey where the crosses represent the players and dashed lines represent their formation:

The ideas that other groups developed also sparked a lot of imagination. I really liked the idea one group came up with in relation to Netball. They imagined what the sport would look like if there were 3 baskets of different heights (each worth different points) instead of just one. Like us, they also looked at the layout of the court but decided to make it larger, to encourage more changeover throughout the match.

This was an extremely engaging workshop which really allowed me to see sport from a different perspective than how I usually would (as very structured and fixed). As we have discovered, mathematics is not always fixed and there are often many ways of doing mathematics. I think this is a lesson I would like to look at in the future as a teacher – to allow the pupils to experiment with sports that they love (see previous blog post about mathematics in dance) (Coventry, 2017). It is also a great way for the children to understand the links and relevance of mathematics.

References

Coventry, J. (2017) Discovering Maths in Dance. [Blog] Glow. Available at: https://blogs.glowscotland.org.uk/glowblogs/jceportfolio/2017/09/14/discovering-maths-in-dance/ [Accessed 8 Nov. 2017].

Teacher package: Mathematics in sport. (2010). Plus. [online] Available at: https://plus.maths.org/content/teacher-package-mathematics-sport [Accessed 8 Nov. 2017].

The Plus Olympic calendar. (2012). Plus. [online] Available at: https://plus.maths.org/content/plus-olympic-calendar-monday-6th-august [Accessed 8 Nov. 2017].

Thomas, R. (2012). Spinning the perfect serve. Plus. [online] Available at: https://plus.maths.org/content/spinning-perfect-serve [Accessed 8 Nov. 2017].

After our input on chance and probability, I was intrigued to investigate the true meaning of randomness and how this relates to our everyday lives.

Randomness in our lives

Randomness is a concept I found very interesting when researching as I never realised how difficult an idea it is for humans to grasp. As humans, we intuitively use our memories to predict what will happen next, whereas true randomness has no memory of what came before (Bellos, 2010). Although we can make educated guesses as to what is to come based on experience and scientific explanation, we really cannot guarantee an outcome for anything.

A funny example of this, as explained by Bellos (2010), is when Apple CEO Steve Jobs had to change the programming behind the ‘shuffle’ feature on iPods. Customers complained that when they used this feature the songs that played were often from the same album or by the same artist. Yet this is extremely possible with randomness, as it does not consider what has already been played. Steve Jobs responded to this feedback by altering the shuffle feature to make it less random, defying the point of randomness altogether!

So why are humans so bad at understanding the concept of randomness?

It is in fact because we have no control over it! As humans, our natural instinct is to give explanations for what happens in our lives – by projecting patterns – and having control in our situations (Bellos, 2010).

I think this relates to the problem humans have when they blame their situations to bad or good luck. Some of us are so invested into the ideas of karma or superstition that we start to lose sight of all the various factors which contribute to our fortunes/misfortunes. Although we might be reluctant to admit it, the random occurrences we encounter come down to chance (Lane, 2011).

An interesting discovery based on luck however, is that “people who believe they are more lucky, are actually likely to be more lucky, because they are more willing to take advantage of opportunities” (Lane, 2011). Furthermore, after carrying out research over several years, Wiseman, (2003) suggests that good luck and bad luck come down to our behaviour and attitudes more than anything else. He explains that lucky people generate good fortune through four basic principles: creating and noticing chance opportunities, listening to their intuitions, having positive expectations, and adopting a resilient attitude (Wiseman, 2003).

It is important to note here that Lane (2011) and Wiseman (2003) suggest that we have control over how we experience a situation rather than have control over the situation itself. For example, someone who considers themselves as lucky may feel lucky about breaking their leg after falling because at least it wasn’t their neck. I think this is where the confusion comes in for humans. We often put a lot of faith in luck, instead of accepting the randomness of events which occur in our lives and facing these events with a positive attitude.

In my opinion, it is not so much the issue that humans do not understand randomness – it’s that we need to accept it! If we accept randomness it is said that we can live a much more carefree and optimistic life (Lane, 2011). It is vital that we teach the concept of probability and chance in school from an early age – not only because it enhances prediction and problem solving skills but so that children can get to grips with this concept and can explore how it relates to their everyday lives (Taylor, n.d.).

Image credit: EX UNO PLURA (2015) (https://www.exunoplura.com/tag/randomness/)

References

Bellos, A. (2010). And now for something completely random. The Daily Mail. [online] Available at: http://www.dailymail.co.uk/home/moslive/article-1334712/Humans-concept-randomness-hard-understand.html [Accessed 16 Oct. 2017].

Lane, M. (2011). Why do we believe in luck?. BBC News: Magazine. [online] Available at: http://www.bbc.co.uk/news/magazine-12934253 [Accessed 16 Oct. 2017].

Taylor, F. (n.d.). Why Teach Probability in the Elementary Classroom?. lamath.org. [online] Available at: http://www.lamath.org/journal/Vol2/taylor.pdf [Accessed 16 Oct. 2017].

Wiseman, R. (2003). Be lucky – it’s an easy skill to learn. The Telegraph. [online] Available at: http://www.telegraph.co.uk/technology/3304496/Be-lucky-its-an-easy-skill-to-learn.html [Accessed 16 Oct. 2017].