After receiving our final input today for the Discovering Mathematics module, I realised how much my opinions and misconceptions of mathematics have changed. I wanted to write one final blog post to summarise some of the key discoveries I have made over the course of the semester and the ways in which I will use these discoveries in my teaching practice.
My opinion of mathematics
Before beginning this elective, I was extremely apprehensive about the thought of “doing mathematics”. What I mean by this is that I always viewed mathematics as complicated sums and equations which needed to be solved. I saw mathematics as a stand alone subject because my teachers never made explicit links to the mathematics I was learning and other curricular areas or the wider world. Now, after researching and questioning the mathematics in everyday life – such as in sport, music, art and games – I understand that maths really is everywhere! Even though the links to everyday life and maths may not be explicit, it is evident the importance that basic mathematical principles hold in so many aspects of life. My favourite example of this is the idea of thinking strategically, which is something I have always done when playing a board game for example, but I’ve never considered this to be a mathematical skill.
My favourite discoveries
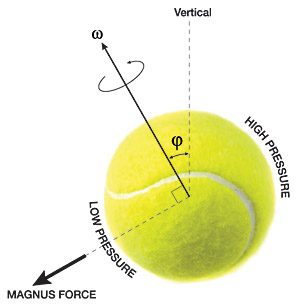
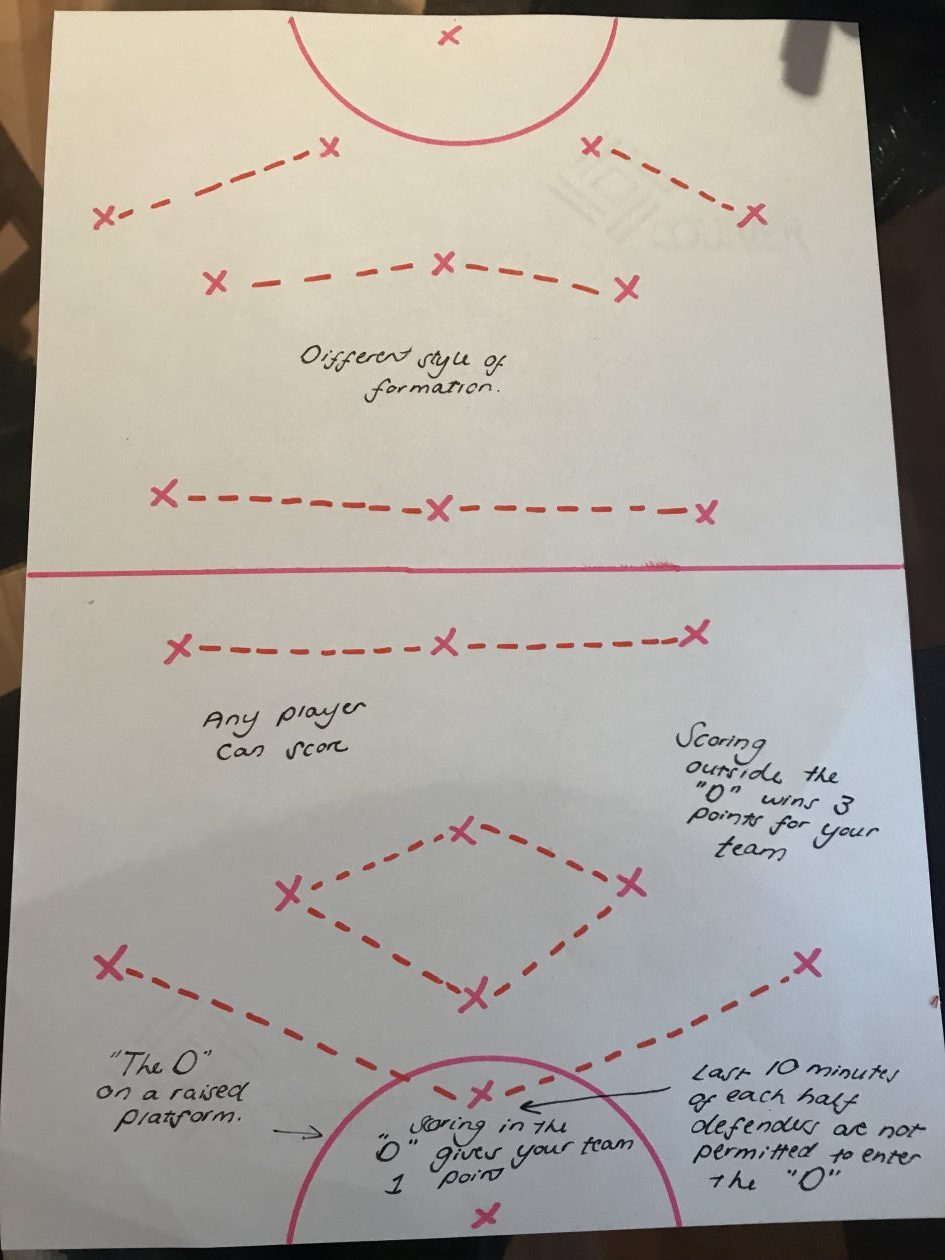
One of my favourite discoveries I made during this module is the link between mathematics and sport. I particularly enjoyed thinking about the mathematics involved in the rules of sport and then reinventing these rules, using the mathematical principles I had identified (Coventry, 2017, a). This is an example of one of the moments when I realised I was really using mathematics rather than simply doing it to solve an equation. I also liked that I could relate mathematics to a dancing – a hobby I’ve enjoyed from an early age. Never did I think I’d be able to relate a passion of mine to a subject I never thought I’d use outside school (Coventry, 2017, b).
How this will influence my teaching practice
Going forward, I am excited to use some of the experiments and examples we have used in class in my own classroom with pupils. In particular I would love them to try and make links to mathematical principles and something they are passionate about such as a sport or a game. This will show the pupils that mathematics is relevant in their lives outside school. I will also be aware of the way I teach mathematics, making sure I issue work which is meaningful and enjoyable for the pupils. A good example I could look at with an upper years class is allowing them to practice their budgeting and money handling skills whilst looking at food chain supply (Sloan, 2017). This would allow pupils to work together in teams to decide what they want to spend their money on, whilst using basic arithmetic to calculate the profit they would make. This is something I feel as though children would become very invested in as they try and beat other groups to make the most money. This could also be a challenge which could be spread across an entire term, with prices for stock changing throughout the duration of the process.
This module has really opened my eyes to the ways in which maths can be explored in wide and meaningful contexts. It has also highlighted the issue that too often people presume they cannot do maths without thinking about what they do in everyday life which is underpinned by mathematical theory and practice. It is therefore vital for me, as a teacher, to make these links explicit to children so they can develop their interest in mathematics throughout their education and beyond.
References
Coventry, J. (2017, a) Discovering Maths in Sport. [Blog] Glow. Available at: https://blogs.glowscotland.org.uk/glowblogs/jceportfolio/2017/11/08/discovering-maths-in-sport/ [Accessed 28 Nov. 2017].
Coventry, J. (2017, b) Discovering Maths in Dance. [Blog] Glow. Available at: https://blogs.glowscotland.org.uk/glowblogs/jceportfolio/2017/09/14/discovering-maths-in-dance/ [Accessed 28 Nov. 2017]
Sloan, A. (2017) The Apprentice Activity. [Blog] Glow. Available at: https://blogs.glowscotland.org.uk/glowblogs/ahseportfolio/2017/11/16/the-apprentice-activity/ [Accessed 28 Nov. 2017]