………….and the answer is Henry the eighth ……….a Mr Hunter joke!
In maths, this week, we’ve been learning all about Fractions. Fractions are a ‘part of’ something. For example, in a football match there is a first ‘half’ and a second ‘half’. When we talk about time, we say ‘quarter’ past/to the hour and ‘half’ past the hour. As you can see fractions are all around us and we use them without ever really stopping to think.
Equivalent Fractions
We have been looking at equivalent fractions, simplification of fractions and fractions of quantities. Here’s what we have been finding out.
Imagine, Mr Hunter wants half a pizza, but the pizza is cut into four pieces, how many pieces should he eat?

Through discussion, we decided that getting one half of a pizza is the same as getting two quarters of the pizza. At least, Mr Hunter will munch down the same amount of pizza either way! This is what we mean when we say:
The fractions 

The word equivalent means, ‘equal’ or ‘same value’. So equivalent fractions are fractions which are equal and with the same value. Although we didn’t have any pizzas, we did use chocolate cubes to work out our equivalent fractions. Here’s another example:
Mr Hunter has a chocolate bar and he divided it into 6 parts. The class get two parts, so our share is two sixths.

Now imagine that the chocolate bar is divided into nine pieces and the class get three pieces. Now, we have three ninths, but when you look at both pictures, we still have the same amount of chocolate. Therefore, we can say that
the fractions 

Simplifying Fractions
We’ve also been looking at how to simplify fractions. Simplifying (or reducing) fractions means to make the fraction as simple as possible.
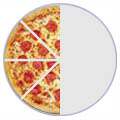
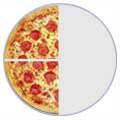
Why say four-eighths or two quarters of a pizza when we really mean half?
| 4/8 | ==> | 2/4 | ==> | 1/2 | ||
| (Four-Eighths) | (Two-Quarters) | (One-Half) | ||||
 |
 |
 |
So, how do we simplify a Fraction ?
Firstly, we tried to evenly divide both the top (numerator) and bottom (denominator) of the fraction by 2 and by 2 again and finally by 3 until we couldn’t go any further. So the fraction simplifies to two-ninths (2/9).
| ÷ 2 | ÷ 2 | ÷ 3 | ||||
| 24 | = | 12 | = | 6 | = | 2 |
| 108 | 54 | 27 | 9 | |||
| ÷ 2 | ÷ 2 | ÷ 3 | ||||
Next week, it’s Money Week, so we are going to be looking at bank accounts and Needs and Wants. Watch this space – it should be exciting.
By Primary 7










