Tag Archives: Binary

1. Computer Systems, Revision

Calculations in computer systems

I was sure I had this here already but I can’t find it.

Here are the main formula we used in the computer systems unit

  • Largest number with n bits = 2n-1
  • No of memory locations/different colours = 2n
  • Coloumn heading in a binary number at n bit =2n-1
  • Size of bitmap = no. of Horizontal pixels X no. of Vertical pixels X Colour Depth
  • No. of pixels = DPI X size in inches
  • Total storage capacity = no. of memory locations X location size.

You should also be able to convert from bits, Bytes, Kilobytes, Megabytes, Gigabytes & Terabytes.

  • Bit= 1/0 (Binary digIT)
  • 1 Byte = 8 Bits
  • 1 Kilobytes= 1024 Bytes  (210)
  • 1 Megabytes= 1024 KB  (220)
  • 1 Gigabytes = 1024 MB  (230)
  • 1 Terabytes = 1024 GB  (240)

For colour depth

  • 8 bits = 256 colours (28)
  • 16 bits = High Colour 65,536 colours (216)
  • 24 bits = True Colour 16,777,216 colours (224)
1. Computer Systems

Homework for Thursday 1st Dec

2 Comments

Answer the following questions.

Convert the following to decimal

  1. 11111100 (2’s comp)
  2. 00110110
  3. 11111111 (2’s comp)

How many pixels in the following files

  1. 320×240 @ 8 bits/pixel
  2. 1024×768 @ 16 bit colour depth
  3. 1280×1024 @ 24bpp

What are the sizes of the following files in bytes

  1. 320×240 @ 8 bits/pixel
  2. 1024×768 @ 16 bit colour depth
  3. 1280×1024 @ 24bpp

Calculate the storage requirements for the following images in Megabytes (to 2 decimal places)

  1. 1440×1080 @ 24 bpp
  2. 1920×1080 @ 24 bpp
  3. 7689×4320 @ 24 bpp
1. Computer Systems, Homework

Binary 2’s Complement

2 Comments

I posted on this last year, I don’t feel the need to go back over it. However, if you would like me to give another full post please just ask.

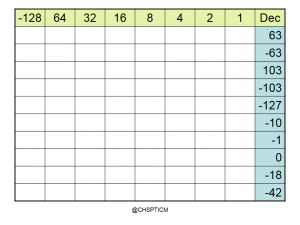
Remember for 8 bit 2’s complement the column headers are -128 64 32 16 8 4 2 1

The homework for tonight is to convert the following to binary using 2’s complement, the answers should be in Bytes so either 8 or 16 bits.

  1. 397
  2. -45
  3. 128
  4. -120
  5. -13
  6. 0
  7. 1013
  8. -92
  9. -100
  10. -3

Have fun

1. Computer Systems, Computing Higher, Standard Grade Computing Studies

Binary Numbers

Computers store all data as binary, numbers are easily stored this way.

Humans work with a base 10 numbering system (we have 10 fingers), however computers can only store data using electricity (on and off) which is base 2.

This article explains binary in a simple way

128  64  32  16  8  4  2  1 are the headings at the top of the binary numbers so 10001000 would be 128+8 which is 136

Practice here before attempting some bingo

For you exams you will be required to show the working for binary conversion, however, you can check this by using a calculator that has a binary function. The calculator below was found in a local pound shop, you can check if your calculator has binary by checking the buttons for BIN, OCT, DEC, HEX.

You can make a little Binary Calculator with the attached file. The photographs show it in action, simply fold the flaps to make the binary number and add the numbers shown. (teachers note that for 2’s complement just change +128 to -128)