Reflecting on my school experiences I realised I didn’t have one that really stood out to me from primary school (not unless you include the trip to the National Museum of Scotland when one of my classmates got their head stuck in a fancy-dress costume!) So instead I thought about memorable high school experiences and one immediately sprung to mind – the Class Act playwriting project.
This was a project I participated in during my sixth year of school as part of my Advanced Higher English class. We were lucky enough to be partnered with the Traverse Theatre Company who work with a few schools across Edinburgh to help pupils develop their playwriting skills. The theatre company provide in-class workshops, giving hints and tips on how to come up with new ideas for a play and how to write them in a way that entices the reader.
After these workshops our class split into small groups to write our own short screenplays. I still remember the play my group came up with: ‘The American Dream’ – a news reporter who is power hungry for fame and decides to sabotage the American president. The most exciting part of it all was knowing that our screenplay would be performed by actors in the Traverse Theatre. This provided a great motivation for us during the writing process as we knew there would be an amazing end product to the project.
Once the screenplays were finished, we were able to have a dress rehearsal with our actors to make sure they grasped the mood of the play and to make any last-minute adjustments. We then had a trip to the Traverse Theatre where we got to see all our plays come to life on stage with actors, costumes and props. I still remember the nervous, yet excited, feeling when I knew our play was being performed next!
To bring it all together we were also given a published book at the end, which included all of the screenplays performed throughout the night. This was an amazing memory to take home.
Image credit: Thomas (2012) https://plus.maths.org/content/spinning-perfect-serve
As part of my journey in discovering mathematics, I have become aware of the fact that maths really is everywhere. So far, we have touched on maths in art, stories, music, computing, gambling and sport. In particular I’ve enjoyed looking at these aspects from a very open perspective, questioning the mathematical theory behind the subject. This was especially interesting to look at in relation to sport, where we took a step back from the rules of sport and completely reinvented them.
Firstly, it is important to understand how mathematics relates to sport. There are many specific examples, such as The Magnus effect in tennis which relates to how the ball spins as it moves through the air (Thomas, 2012). A similar example can be seen in badminton where the shuttlecock obeys Newton’s laws of motion. Its acceleration is controlled by the downward force of gravity and a “drag force” from the air that is proportional to the square of the shuttlecock’s speed through the air (The Plus Olympic calendar, 2012).
Although these are very specific examples, we can also see how particular aspects of mathematics relate to nearly all sports: the physics of sport,sporting strategy, architecture and infrastructure, predicting results and sporting statistics, scoring and ranking, and betting and odds (Teacher package: Mathematics in sport, 2010).
Something which we considered during our workshop was whether the popular sports we know well are structured in the best way possible. My group looked at the example of hockey. At first we struggled to come up with ways of improving the sport as we already thought that the rules and strategies of the sport were fair. Then we were posed with the question: what would make hockey more exciting watch? This started to make us think more creatively…
Firstly, we thought about the pitch layout – like most pitches the hockey field is flat. We considered increasing the difficulty of the sport by raising the surface of the area where the goal is (this area is known as the “D” due to its shape – another mathematical link!) If there was a platform of even just a few inches, this would require the players to be able to lift (or chip) the ball and retain control quickly after to avoid defenders “stealing” the ball. One of the key rules for hockey is that you are only allowed to score when you are in the “D”. We thought the game would be more exciting if players were able to score from anywhere on the pitch, meaning that defenders would always need to be alert. We thought we could also change the scoring system so that if players score outside the “D” they can win their team 3 points instead of 1.
Moreover, we thought of a way of motivating players to score more goals. We decided that for the last 10 minutes in each half (hockey is a game of two 35 minutes halves) the defenders would not be allowed to defend inside the “D”. This means that if the player manages to get past the defenders, it is 1v1 scenario with the goal keeper. This would allow the player to show off their scoring skills/abilities.
Below is an illustration of our reinvention of hockey where the crosses represent the players and dashed lines represent their formation:
The ideas that other groups developed also sparked a lot of imagination. I really liked the idea one group came up with in relation to Netball. They imagined what the sport would look like if there were 3 baskets of different heights (each worth different points) instead of just one. Like us, they also looked at the layout of the court but decided to make it larger, to encourage more changeover throughout the match.
This was an extremely engaging workshop which really allowed me to see sport from a different perspective than how I usually would (as very structured and fixed). As we have discovered, mathematics is not always fixed and there are often many ways of doing mathematics. I think this is a lesson I would like to look at in the future as a teacher – to allow the pupils to experiment with sports that they love (see previous blog post about mathematics in dance) (Coventry, 2017). It is also a great way for the children to understand the links and relevance of mathematics.
References
Coventry, J. (2017) Discovering Maths in Dance. [Blog] Glow. Available at: https://blogs.glowscotland.org.uk/glowblogs/jceportfolio/2017/09/14/discovering-maths-in-dance/ [Accessed 8 Nov. 2017].
Teacher package: Mathematics in sport. (2010). Plus. [online] Available at: https://plus.maths.org/content/teacher-package-mathematics-sport [Accessed 8 Nov. 2017].
The Plus Olympic calendar. (2012). Plus. [online] Available at: https://plus.maths.org/content/plus-olympic-calendar-monday-6th-august [Accessed 8 Nov. 2017].
Thomas, R. (2012). Spinning the perfect serve. Plus. [online] Available at: https://plus.maths.org/content/spinning-perfect-serve [Accessed 8 Nov. 2017].
Living in a digital world, I ask the question: do we need to teach pupils how to read an analogue clock in schools?
Although most of us have converted to digital clocks in our online, digital world with our smartphones, computers and televisions; we cannot deny that our encounters with analogue clocks are not completely non-existent. There is an argument that in most places we visit – schools, work offices, supermarkets, restaurants and hotels – we most likely still encounter analogue clocks (Merz, 2014). Therefore, is teaching how to read analogue clocks not a necessary skill to teach pupils in school?
According to Merz (2014), many teachers are frustrated with the idea of this skill being disregarded, with the argument that analogue clocks can provide a vivid representation of time that digital clocks cannot – which can aide visual learners. Analogue clocks can also teach concepts including time management, the passage of time and how much time we have left to complete something (Merz, 2014).
However, with our fast-developing technological advances, it is difficult not to wonder if eventually analogue clocks will disappear in our society. Nowadays, we see plasma screen televisions or digital billboards nearly everywhere we go – displaying digital time. Although analogue clocks are often visually appealing and provide nice décor, they don’t really provide any use other than telling the time. It is therefore arguable that digital screens are much more valuable in society as they are multi-purposeful and allow for more creativity (The benefits of digital billboard advertising, 2015). For example, recently in a shopping centre in Edinburgh, I passed a large television screen which displayed the current top news stories, multiple adverts for new products which could be found in the centre, whilst also displaying the time.
Moreover, one of the key issues with teaching pupils about the analogue clock in schools, is how complex it is for pupils to grasp and understand. This light-hearted, comical video highlights the difficulties for young learners learning how to read time:
(Dave Allen – “Teaching Your Kid Time” – ’93 – stereo HQ., 2009)
I partly decided to write this blog post as I was one of the learners in primary school who had difficulties learning about time. I could not wrap my head around the idea of ‘quarter past’, ‘half past’ and ‘quarter to’ (considering we represented every other number on the clock as a number). I also struggled with the concept that there were different ways of reading the clock (e.g. saying 35 past 7 or 25 to 8) which would both be correct. This raises key issues of problem solving and looking at a mathematical concept from multiple perspectives (key skills which are transferrable across all mathematical topics.)
It is important to note that these are aspects of telling the time which apply to both reading the analogue AND digital clock. It is therefore my opinion that the real issue with teaching time to pupils is the concept itself, rather than teaching pupils how to read a particular type of clock. The video above does highlight the difficulties of learning to read an analogue clock – however with the fundamental understanding of the concept of telling the time, I believe that most pupils would welcome the challenge of applying their knowledge to reading an analogue clock. For example, it is vital that children have a strong understanding that 6 is half of 12 to be able to understand why we use the term half past. Another skill which would benefit children before reading an analogue clock is knowing the 5 times table. According to Drabble (2013), without knowing the 5 times table, “anything beyond the o’clocks becomes almost unotainable.” This relates to the idea of longitudinal coherence, introduced by Ma (1999) who states that teachers should use children’s prior knowledge to enhance learning in the topic at hand. It also links with what she writes about basic ideas, meaning that children should revisit the basic concepts they have learned (i.e. fractions and times tables) to understand that they are required for other areas of mathematics (Ma, 1999).
In conclusion, after doing research online and through my own experiences, I believe there is a necessity for teaching pupils about digital and analogue clocks. I believe that we currently live in a world where analogue and digital clocks are both relevant and should therefore both be exposed to pupils. I have realised since studying this issue, that it is important to ensure that pupils understand the principles behind telling the time before introducing them to an analogue OR a digital clock. Furthermore, learning how to read two types of clocks reinforces pupils’ understanding about the concept of time and allows them to practice telling the time from different contexts. This reflects the work of Ma (1999), who highlights the importance of connectedness – meaning that children can link what they have learned to different contexts.
This picture reflects what I saw on my first year placement and shows how to make reading the time on an analogue clock more visually appealing for pupils, whilst also acting as a visual aide (however it is important that pupils realise that they cannot rely on this, as every other analogue clock they see will not be represented in this way!):
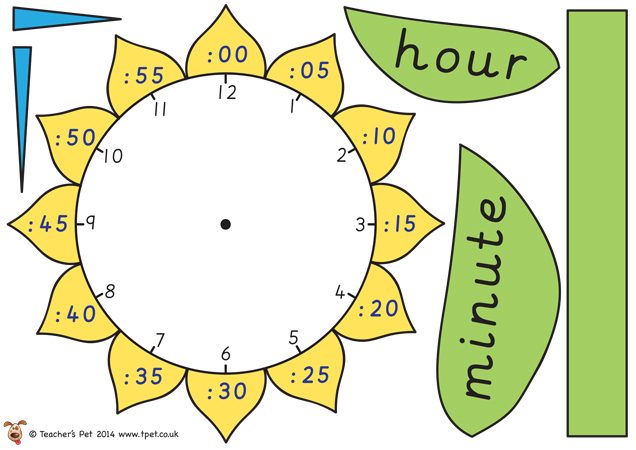
Image credit: Teacher’s Pet (2014) www.tpet.co.uk (http://displays.tpet.co.uk/?resource=1507#/ViewResource/id1507)
References
Dave Allen – “Teaching Your Kid Time” – ’93 – stereo HQ. (2009). (Video) YouTube: davidwrightatloppers.
Drabble, E. (2013). How to teach … telling the time. The Guardian. [online] Available at: https://www.theguardian.com/education/teacher-blog/2013/aug/05/telling-the-time-teaching-resources [Accessed 4 Nov. 2017].
Ma, L. (1999). Knowing and teaching elementary mathematics : teachers’ understanding of fundamental mathematics in China and the United States. Mahwah, N.J.: Lawrence Erlbaum Associates.
Merz, S. (2014). Should We Still Teach Analog Clocks?. [Blog] Stories From Schoolaz. Available at: http://www.storiesfromschoolaz.org/still-teach-analog-clocks/ [Accessed 4 Nov. 2017].
The benefits of digital billboard advertising. (2015). [Blog] Signkick. Available at: http://www.signkick.co.uk/blog/the-benefits-of-digital-billboard-advertising/ [Accessed 4 Nov. 2017].
Glow Blogs uses cookies to enhance your experience on our service. By using this service or
closing this message you consent to our use of those cookies. Please read our Cookie Policy.
