In workshop, we were looking at the mathematics behind puzzles and board games. One of the games we looked at was Sudoku. People argue that there is no arithmetic in Sudoku as there’s no adding or calculations necessary. However, surely being able to look at patterns and sequences across the Sudoku square is using basic mathematical principles since maths is about seeing patterns in nature (Sawyer, 1955, cited in Boaler (2010, p.17). Furthermore, it does involve problem solving. Alternatively, it could be viewed that it Is just a process of elimination since you could use shapes, animals or letters instead of numbers but this would still involve analysing patterns.
The board game that I chose to look at for the workshop was Monopoly as there have been many summers when my friends and I have spent hours trying to win at Monopoly and now I’ve discovered that maths can help me win!
When I played monopoly, the only I thought I gave to the mathematics behind it was to buy Park lane, Mayfair and the train stations as once I purchased these, I could build houses. Then when someone landed on my property, I would get a considerate amount of money from people owing me rent (although I wasn’t fully aware that this was going back to basic mathematical principles (Ma, 2010, p. 104). The thrill of this was one of the most exciting parts of the game! I was looking at buying properties that were worth the most instead of looking into the chance and getting the properties which are the most landed on (standupmaths, 2016)
The basic mathematical concepts that link with Monopoly are chance and probability. This is because when you throw the dice it is up to chance what the outcome is. If you want to learn more about chance and probability visit a previous blog post of mine (Noble, 2017). Other basic concepts used in the game are adding and subtracting as the cashier when calculating rent as well as counting number of squares as you move your object (in my case that was always the dog).
A woman girl from Northern Ireland was crowned the UK champion for Monopoly and she gave some tips as to how you can win at Monopoly which relate to fundamental mathematical concepts (Telegraph, 2015). The basic mathematics of probability explains that Park Lane is actually the least landed on property therefore, I shouldn’t purchase it!
However, I was on the right path to success by buying up all the Railway stations because “…they deliver a more constant level of avenue over the course of the game.” (ShortList, no date). In addition to the stations, it is also best to buy the red properties and the orange ones as these are the top two most landed on properties on the board. They also do not cost much but bring in more money once you put hotels on them (ShortList, no date). However, is it beneficial to always place a hotel on your properties?
In the past, always would have bought four houses and then moved to buying hotels for properties. However, the UK champion of Monopoly says that “Once you’ve reached 3 houses, the amount that the rent increases with each house maxes out.” (Telegraph, 2015). Therefore, fundamental mathematics was used to help figure out the best way to win!
Furthermore, jail is the most commonly landed on place on the board, this is probably because there are several ways in which you can go to jail: landing on go to jail; community chest or chance (standupmaths, 2016). Thus, when you are in jail you should try and stay there for the longest time possible later on in the game (ShortList, no date). This is because other people will have bought up properties, put up houses or hotels. Therefore, the longer you stay in the jail the zero probability or chance you will have of landing on their properties and losing money since you are not moving.
Another interesting point to note is that according to probability, the most rolled number in Monopoly is 7. So, if you are going to place houses on your property you should wait until they are 7 spaces away from your property so that you can win more money (Robitzski, 2017).
(Business Insider, 2015)https://
However, you might think using maths to win ruins the fun but these are still interesting observations. I know in the future when I play monopoly, I am going to apply my mathematical knowledge of chance and probability and what I have learnt from this blog to try and win. For example, I am going to try to purchase the red and orange properties and stay clear of buying park lane!
References:
Boaler, J. (2010) The elephant in the classroom: helping children learn and love maths. London: Souvenir Press.
Robitzski, D. (2017) How to Crush Your Friends at Monopoly Using Math. Available at: https://www.inverse.com/article/32781-win-monopoly-using-math (Accessed: 1 December 2017).
Business Insider (2015) How to use math to win at Monopoly. Available at: https://www.youtube.com/watch?time_continue=108&v=7_SXFtdf65s (Accessed: 1 December 2017).
Ma, L. (2010) Knowing and teaching elementary mathematics: teachers’ understanding of fundamental mathematics in China and United States. (Anniversary Ed.) New York: Routledge.
Noble, R. (2017) ‘Win with maths?’, My teacher journey, 17 October. Available at: https://blogs.glowscotland.org.uk/glowblogs/rsneportfolio/2017/10/17/win-with-maths/ (Accessed 13 November 2017).
ShortList (no date) 17 ways to win at Monopoly every single time. Available at: https://www.shortlist.com/news/17-tips-to-become-a-monopoly-master/50673 (Accessed: 1 December 2017).
standupmaths (2016) The Mathematics of Winning Monopoly. Available at: https://www.youtube.com/watch?v=ubQXz5RBBtU (Accessed: 1 December 2017).
Telegraph Reporters (2015) ‘How to always win at Monopoly: seven essential tips’, The Telegraph, 21 July. Available at: http://www.telegraph.co.uk/men/the-filter/how-to-always-win-at-monopoly-seven-essential-tips/ (Accessed: 1 December 2017).

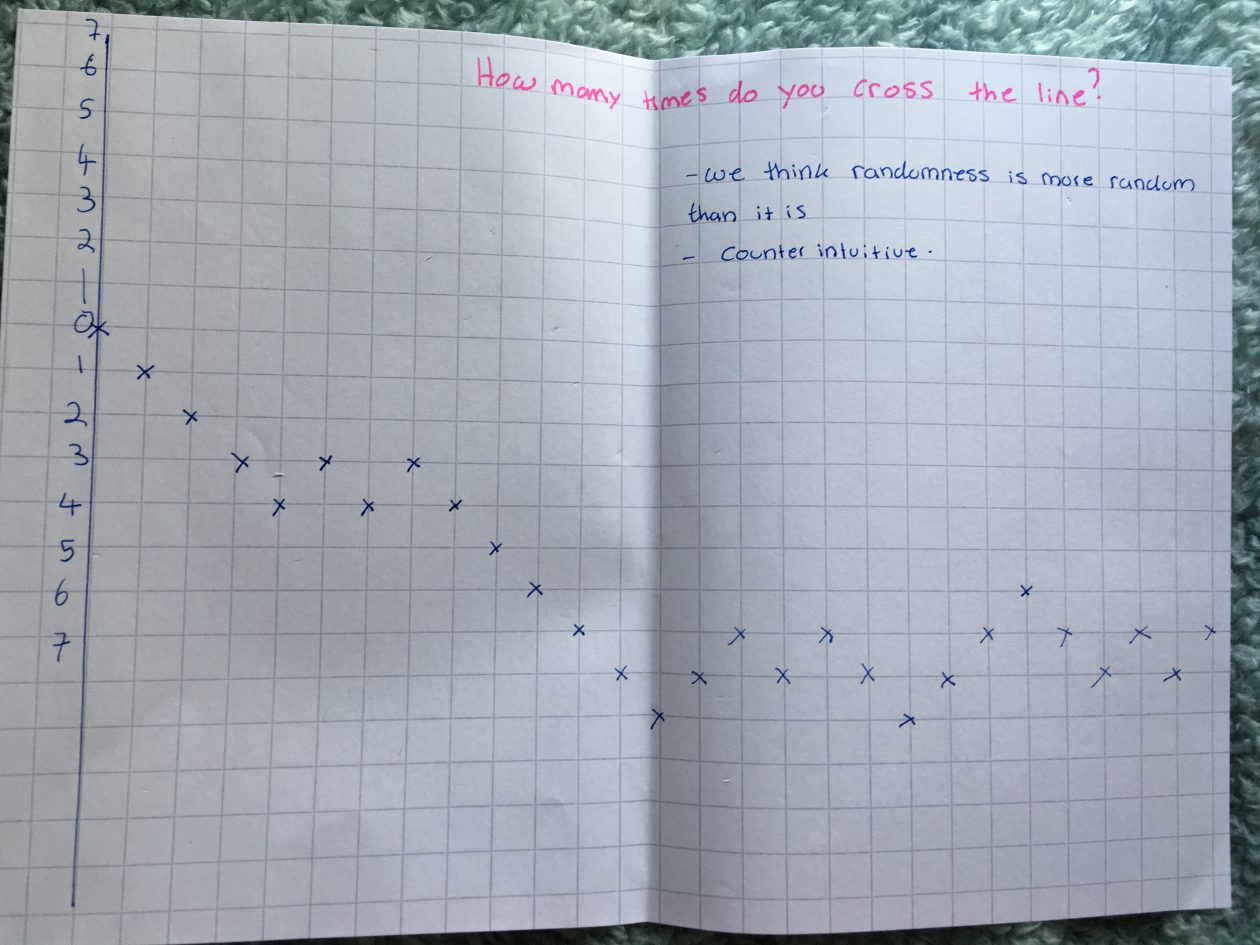
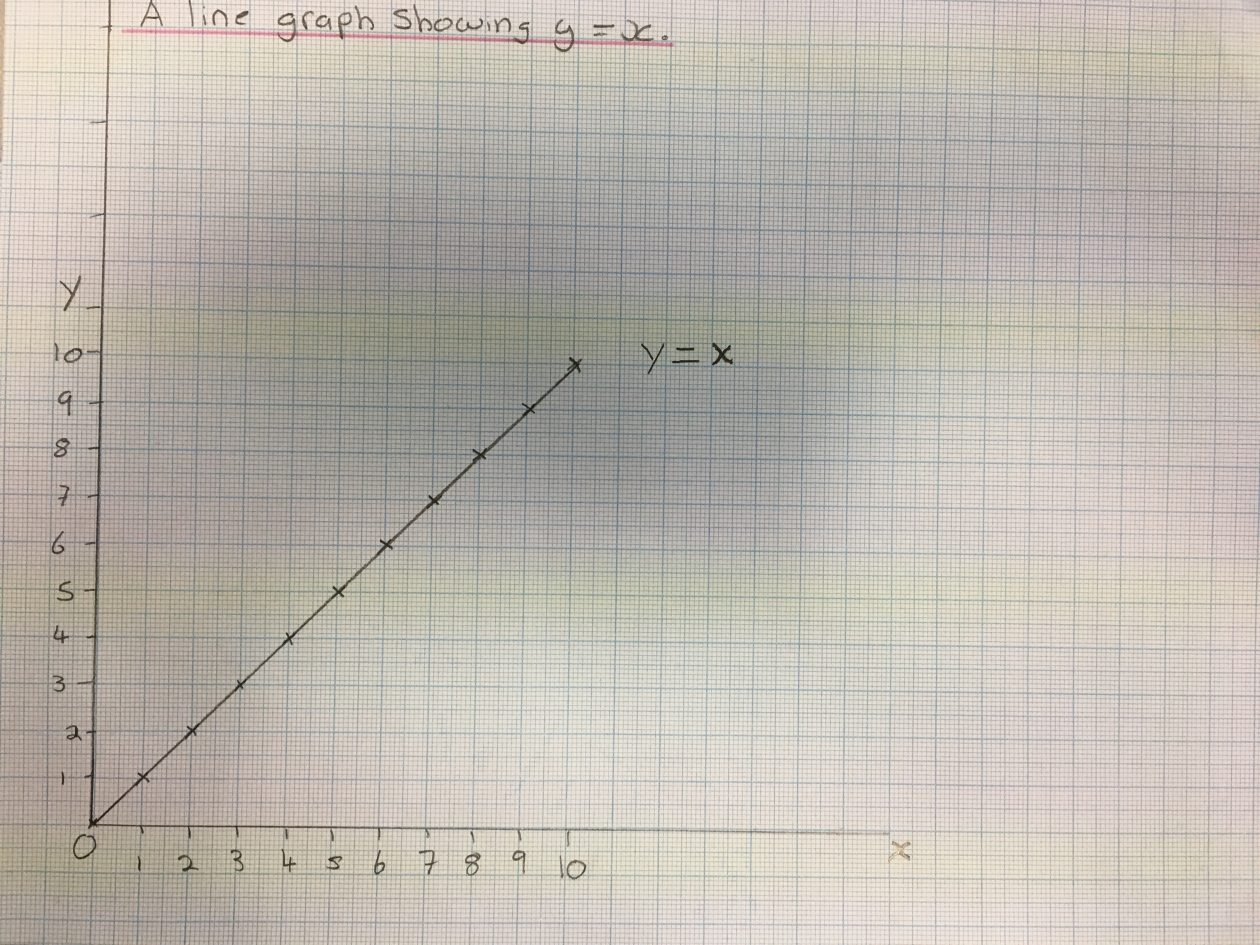 g out of 10. Therefore, we demonstrated knowledge of fundamental understanding of mathematics as we used basic concepts and connecting them together in order to make relationships and associations between the graphs (Ma, 2010, p.104).
g out of 10. Therefore, we demonstrated knowledge of fundamental understanding of mathematics as we used basic concepts and connecting them together in order to make relationships and associations between the graphs (Ma, 2010, p.104).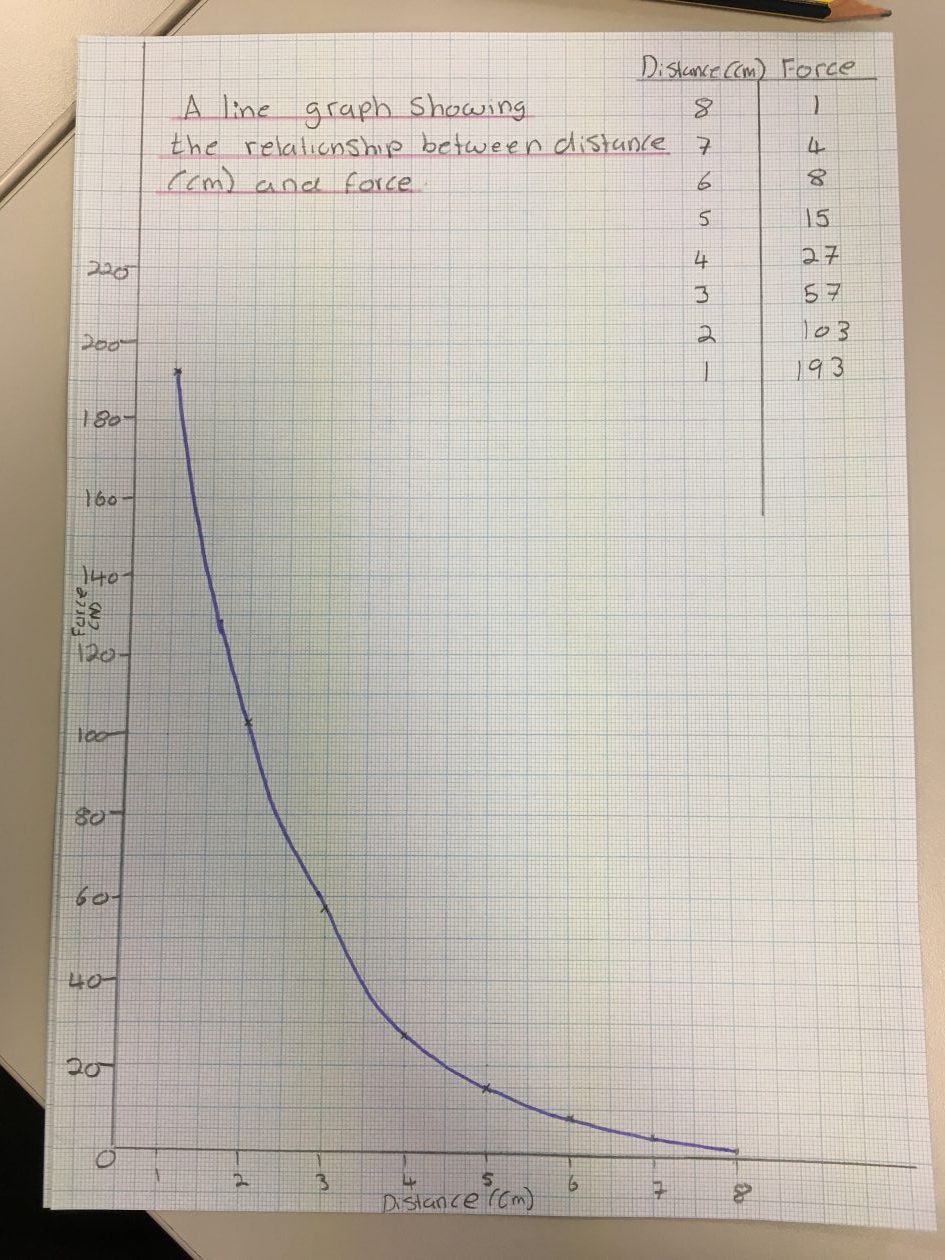
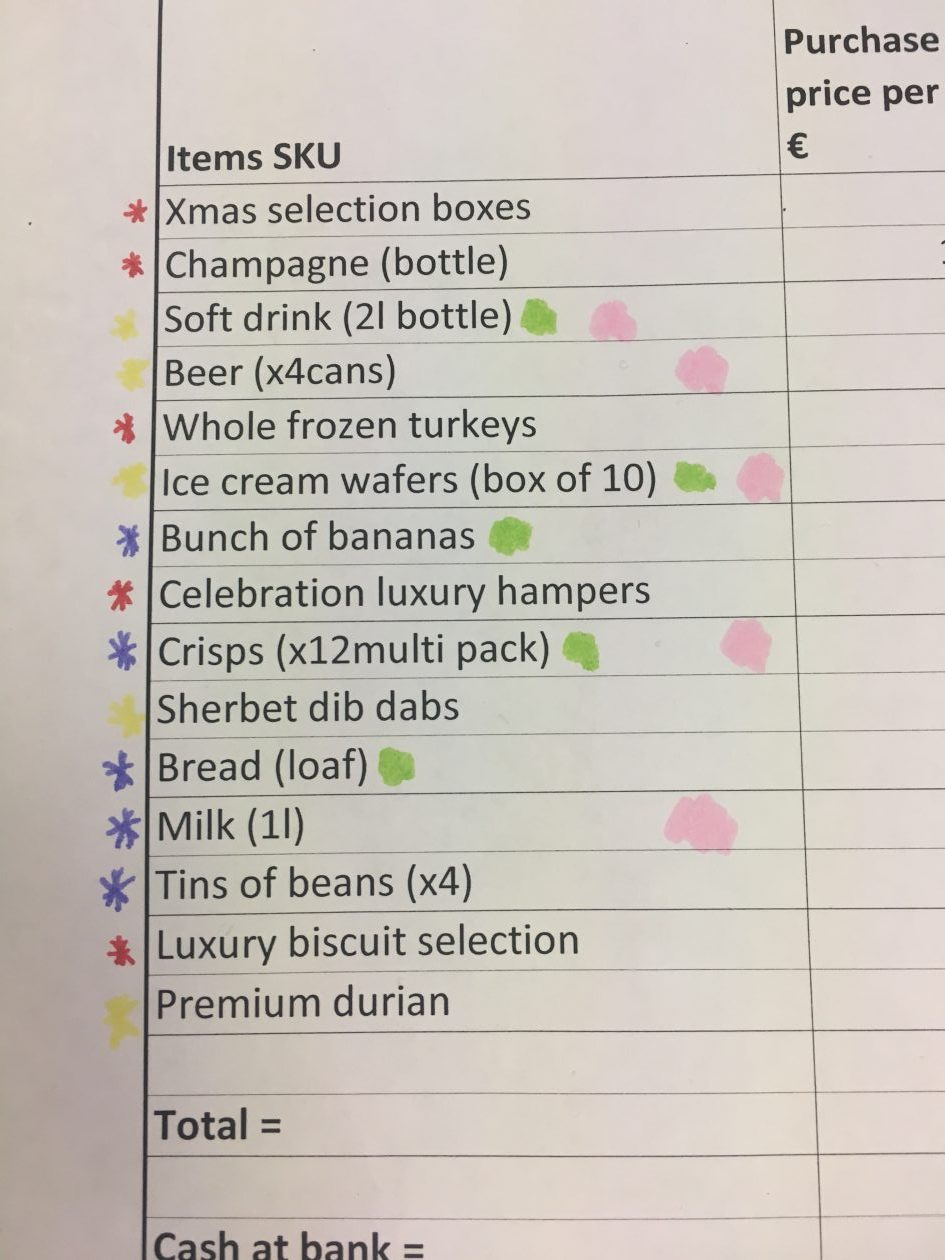
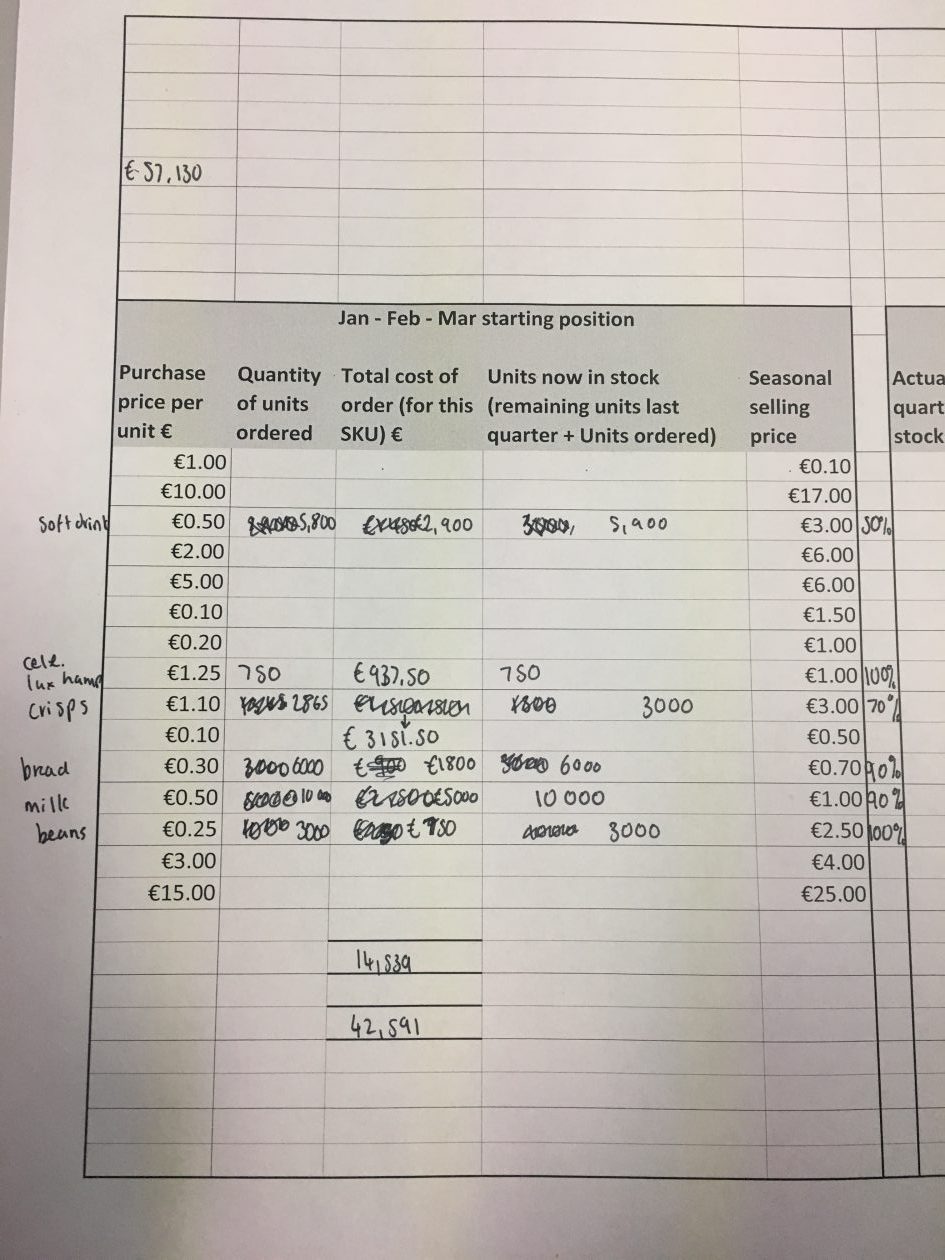
 Furthermore, junior doctors are expected have a profound understanding of fundamental mathematics as they are to know ratios and statistics to do with for example, the risk and probabilities of what one single cigarette can do to you (Hothersall, 2016). Therefore, this part of medicine involves several basic concepts of mathematics such as probabilities, ratio, change and recording (Ma, 2010, p.104). Even breaking your leg requires knowledge of the basic concepts as it’s due to forces and the angle, the speed that something might hit your leg at to break it (Porta, D.J).
Furthermore, junior doctors are expected have a profound understanding of fundamental mathematics as they are to know ratios and statistics to do with for example, the risk and probabilities of what one single cigarette can do to you (Hothersall, 2016). Therefore, this part of medicine involves several basic concepts of mathematics such as probabilities, ratio, change and recording (Ma, 2010, p.104). Even breaking your leg requires knowledge of the basic concepts as it’s due to forces and the angle, the speed that something might hit your leg at to break it (Porta, D.J).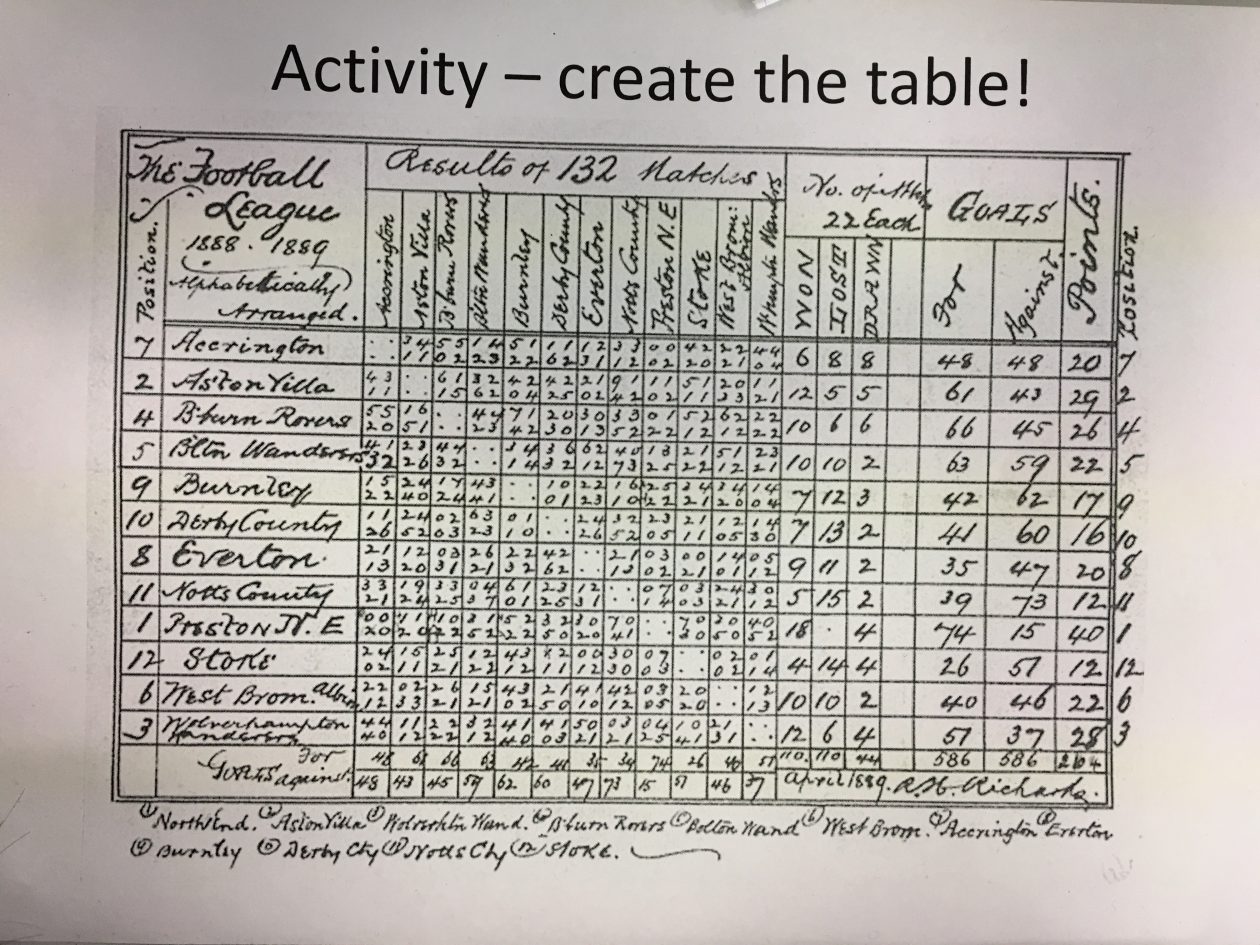
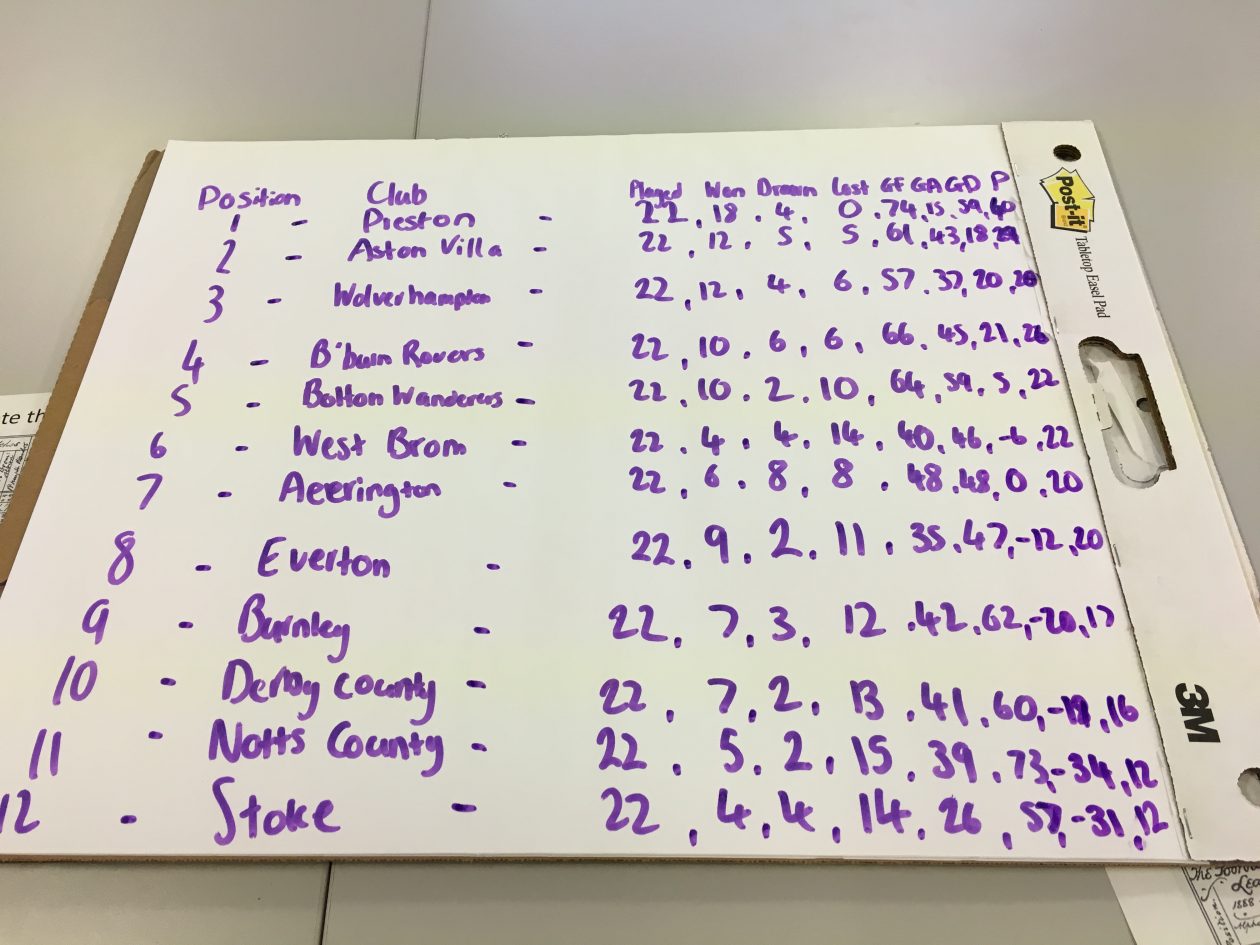 We decided to order the football clubs from top to bottom according to the most points a club had won. We used basic mathematical principles (Ma. 2010, p. 104) of counting to find out how many games each team had won, drawn or lost. To work out the goal difference we used the basic mathematical concept of subtraction, subtracting the goals against from goals for.
We decided to order the football clubs from top to bottom according to the most points a club had won. We used basic mathematical principles (Ma. 2010, p. 104) of counting to find out how many games each team had won, drawn or lost. To work out the goal difference we used the basic mathematical concept of subtraction, subtracting the goals against from goals for. Next, we designed our own sports game and looked at how maths was applied to the sport. Our sport was called Smack-ball. It was based on the memory of a game many people have played. This being, when you have a balloon you try and keep the balloon up in the air by hitting the balloon as it comes back down and you can’t let it touch the ground. So, essentially, smack-ball involves using a ball that is the size of your hand-span and it weighs 196 grams. The court will be rectangular, 10m by 5m, the shorter walls are the goals, there are three players on each team and the game lasts 10 minutes. The aim is to try and smack the ball (involving passes to your other team members) towards your teams wall without letting the opposite team intercept the ball.
Next, we designed our own sports game and looked at how maths was applied to the sport. Our sport was called Smack-ball. It was based on the memory of a game many people have played. This being, when you have a balloon you try and keep the balloon up in the air by hitting the balloon as it comes back down and you can’t let it touch the ground. So, essentially, smack-ball involves using a ball that is the size of your hand-span and it weighs 196 grams. The court will be rectangular, 10m by 5m, the shorter walls are the goals, there are three players on each team and the game lasts 10 minutes. The aim is to try and smack the ball (involving passes to your other team members) towards your teams wall without letting the opposite team intercept the ball.