In this blog post, I am going to talk about the learning experience of using artefacts to teach about the child evacuees during the war. I am going to be writing this from the learners point of view as well as making reference to ideas for teaching from a teacher’s perspective. Although this workshop was focused on drama it linked to using artefacts to teach social studies and subject areas in the wider curriculum. Additionally, through social studies, I have learned that artefacts can be historical and cultural according to (Pickford, Garner and Jackson, 2013) and artefacts are primary resources (Hoodless et al. 2008), meaning that they are from the time that is being investigated. In the workshop, I was investigating a persons suitcase from the time of the war (at the time we were not told it was a child’s).
The reason why this workshop interested me on this day was because of the artefacts used for the teaching and learning. It had never occurred to me to use artefacts for lessons nor have I even been taught a history lesson or any lesson in this way as I always had to learn from a textbook or worksheets. Additionally, during this workshop I connected with the person behind the suitcase and I gained an interest into wanting to knowing more about it.
Significantly, our tutor told us that when she taught a class using this artefact the children believed that this was a real suitcase, can you imagine the excitement? Therefore, as a student learner and future teacher in this case, even though the suitcase was not legitimate, I used my imagination which is involved when investigating artefacts (Pickford, Garner and Jackson, 2013), but I used it to imagining that thus suitcase was real as if I was a child in the class.
The artefact presented was a child evacuees suitcase from the time of the war. For me, this artefact brought the history to life. It made it all real for me and the fact that this artefact (in my imagination) was a primary source that I was able to hold and touch.
In another workshop I got to touch authentic archives from the time of the Tay Bridge disaster and because it was real, i got the feeling of awe but it was also an eerie feeling. Once I saw the items I thought … this was real, that was in someone’s pocket who died during this disaster, they put that there but why? Was his poem special? Why was it there? Who was this person? Why were they on the train? Did they have a family? Likewise, I think had the suitcase been real I would definitely would have had the same response. As I investigated the suitcase, I had similar questions such as who owned this suitcase, what age were they, where were they going and once i learned it was an evacuees suitcase my questions turned to how did they feel, did they realise what was going on, was their home okay, what kind of clothing did they wear back then, what year did this happen in, did they survive?
For me, it was looking at the primary sources or artifacts was what made me feel empathetic about what happened. I felt emotionally involved due to a feeling of connection to the events happened in the past even though i know no one from these events such as the war. As a future teacher, I have realised that in order to develop children or learners’ empathy I will need to demonstrate that the people that the learners are learning about, are real people as well as encouraging them to look at different views and perspectives (The Historical Association, 2007; Hendrickson (2016). Whilst imagining that the artefact was real, it amazed me (Turner-Bisset, 2005) so I can only imagine how eager the children in my tutors class would have been to hold it. However, had it been authentic, it would have been such a wow experience for me as a learner especially since I could touch the artefact myself and it would transport and connect me to the past (Hoodless et al., 2008), a person in the past enhancing the fact that this was a this real event!
The group I was in for investigating the archives from the Tay Bridge disaster got the insurance claim pages and we were to investigate what they were. We worked as a collaborative group, developing our thinking skills. This involved working together and problem solving to reach a conclusion (Hoodless et al. 2009; Tunnard and Sharp, 2009). I learned more from listening to others at the table who were bouncing ideas and thoughts off of each other and sharing them than I would have by myself (Hoodless, et al. 2008; Hoodless, et al. 2009; Tunnard and Sharp, 2009, Bowen, 2013). However, since I was unsure what the source could have been, I did not really join the discussion much so I Just listened to other members of the group. Having investigated it, we discovered that the writing was cursive, it was like old handwriting, there were names of staff workers and of people of various ages, a date which was the day after the Tay Bridge Disaster and certain amounts of money. It is crucial to note that even though collaborative learning was used to investigate archives, it can be used to investigate artefacts too (Bowen, 2013)
However, I found this artefact quite challenging to interpret whilst others did not. Therefore, when it came to group discussion of what prior knowledge we would give learners as teachers, I think that more prior knowledge should have been given to this artefact as a learner may not know what an insurance claim is or what one looks like.
Furthermore, I (as the learner) was a real historical detective (Cooper, 2000; Turner-Bisset, 2005), as I was investigating for myself what had happened, in both classes thus, furthering my own learning. Often when I have not known about something in the past, I’ve gone and researched it myself. Although I am never planning on rhyming off details and facts, I always found that after simply just reading and being interested in it or investigating it myself, I remembered what I had researched myself effortlessly (Pickford, Garner and Jackson, 2013).
Barlow (2013) would argue that teachers need to be careful when looking at everyday things for social studies learning as if you are starting with the children’s world, it can be quite challenging to make it exciting since it is not new. In this case, one could question whether teachers should provide familiar artefacts for relevance or would it be better to provide mysterious and unfamiliar artefacts? Barlow (2013) recommends using something unusual or less familiar to gain learners interest and engagement. I understand this point of view however, I believe that as a learner the history is made interesting because of the emotion and the people behind it rather than how familiar or unfamiliar the artefact might be .
During another workshop, we discussed the idea of creating excitement and engagement in the learning by teachers wrapping up artefact, keeping them hidden from the children (Turner-Bisset, 2005). I think this would be an excellent practice in the classroom because even though we were given a sheet of paper and told not to turn it over, all you want to do is turn it over, you are excited and want to see what is hidden likewise, there would be even more excitement if there is an object wrapped up and the teacher instructs you not to unwrap it yet… as a learner i know i would definitely be excited to unwrap it and find out what is in there.
Teacher points:
- Need to be careful planning for selection of artefacts
- Encourage children to see the human side of the story, to be able to connect with the past and develop empathy
- let the learners do history like a historian would
- Let children handle the objects
- Use collaborative group work for investigations but avoid learners in the group being passive, each person could have a certain task to do
- Artefacts could be used in the wider curriculum to stimulate interest or discussion (Scoffham, 2013; Clough and Newman, 1999)
- When teaching, I could even use a local archive place to borrow artefacts for lessons
Learner points:
- Artefacts stimulate learning, curiosity and discussions
- Collaborative working means sharing of ideas
- Connect with how people might have felt back then. What would I feel like if I had a family member on that train?
- What might I have had in my suitcase during the evacuee time?
References:
Barlow, A. (2013) ‘Geography and history in the local area’, in Scoffham, S. (ed.) Teaching Geography Creatively. London: Routledge, pp. 100-111.
Bowen, P. (2013) ‘History’, in Jones, R. and Wyse, D. (eds.) Creativity in the Primary Curriculum. 2nd edn. London: Routledge, pp. 116-129.
Cooper, H. (2000) The Teaching of History in Primary Schools: Implementing the Revised National Curriculum. 3rd edn. London: David Fulton Publishers ltd.
Clough, N. and Newman, L. (1999) ‘Using artefacts to support children’s learning in religious education’, in Ashley, M. (ed.) Improving Teaching and Learning in the Humanities. London: Falmer Press, pp. 81-100.
Hendrickson, L. (2016) ‘Teaching with Artifacts and Special Collections’, Bulletin of the History of Medicine, 90(1), pp. 136-140. Available at: https://muse.jhu.edu/article/613425 (Accessed: 17 October 2018).
Hoodless, P. (2008) Teaching History in Primary Schools. Exeter: Learning Matters Ltd.
Hoodless, P., McCreery, E., Bowen, P., and Bermingham, S. (2009) Teaching Humanities in Primary Schools. 2nd edn. Exeter: Learning Matters Ltd.
Pickford, T., Garner, W., and Jackson, E. (2013) Primary Humanities: Learning through Enquiry. London: SAGE Publications Ltd.
Scoffham, S. (2013) Geography and Creativity: Making Connections, in Scoffham, S. (ed.) Teaching Geography Creatively. London: Routledge, pp. 1-13.
The Historical Association (2007) Teaching Emotive and Controversial History 3-19. Available at: https://www.history.org.uk/secondary/resource/780/the-teach-report (Accessed 16 September 2018).
Tunnard, S. and Sharp, J. (2009) ‘Children’s views of collaborative learning’, Education 3-13, 37(2), pp. 159-164. doi: 10.1080/03004270802095421.
Turner-Bisset, R. (2005) Creative Teaching: History in the Primary Classroom. London: David Fulton Publishers.

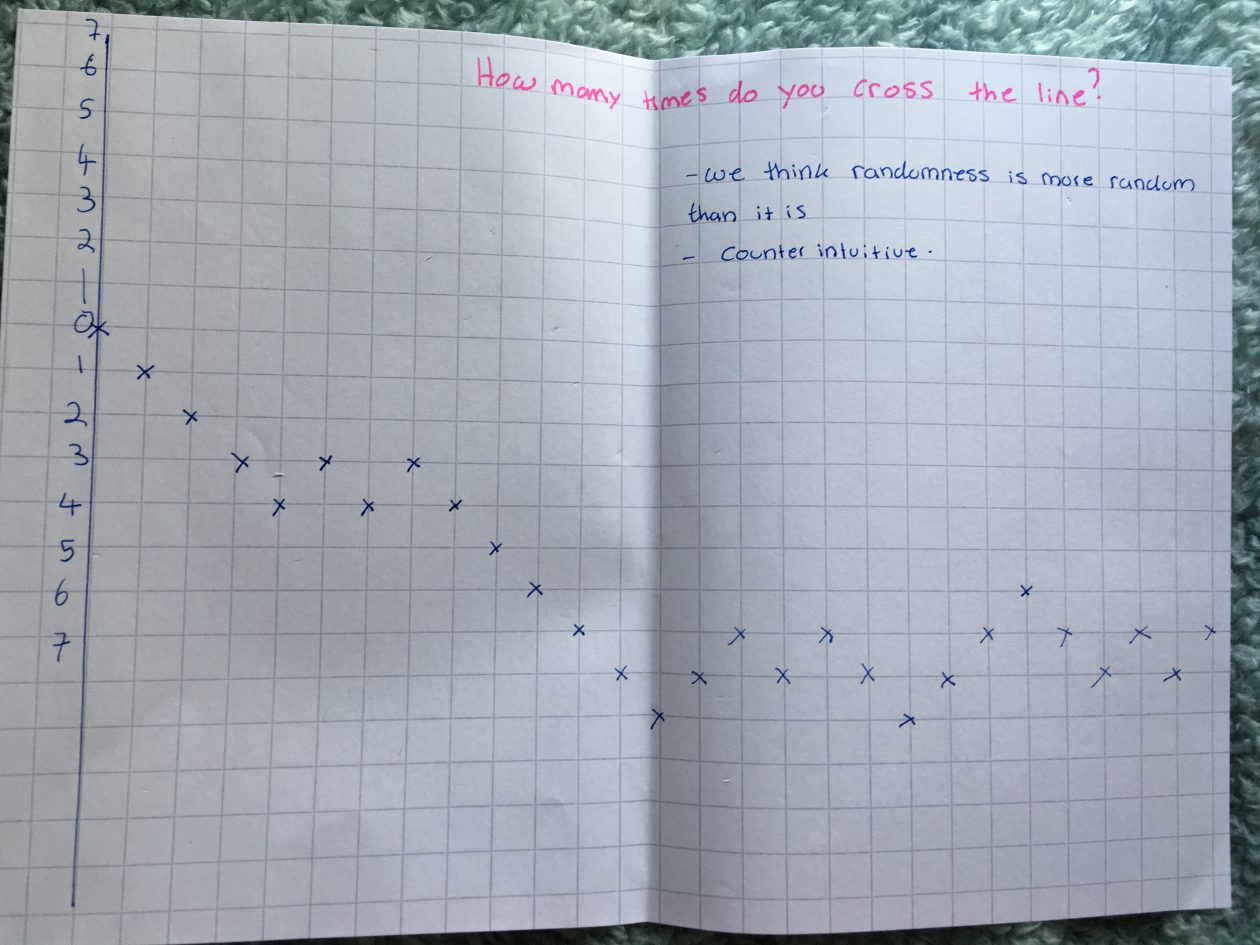
 Furthermore, junior doctors are expected have a profound understanding of fundamental mathematics as they are to know ratios and statistics to do with for example, the risk and probabilities of what one single cigarette can do to you (Hothersall, 2016). Therefore, this part of medicine involves several basic concepts of mathematics such as probabilities, ratio, change and recording (Ma, 2010, p.104). Even breaking your leg requires knowledge of the basic concepts as it’s due to forces and the angle, the speed that something might hit your leg at to break it (Porta, D.J).
Furthermore, junior doctors are expected have a profound understanding of fundamental mathematics as they are to know ratios and statistics to do with for example, the risk and probabilities of what one single cigarette can do to you (Hothersall, 2016). Therefore, this part of medicine involves several basic concepts of mathematics such as probabilities, ratio, change and recording (Ma, 2010, p.104). Even breaking your leg requires knowledge of the basic concepts as it’s due to forces and the angle, the speed that something might hit your leg at to break it (Porta, D.J).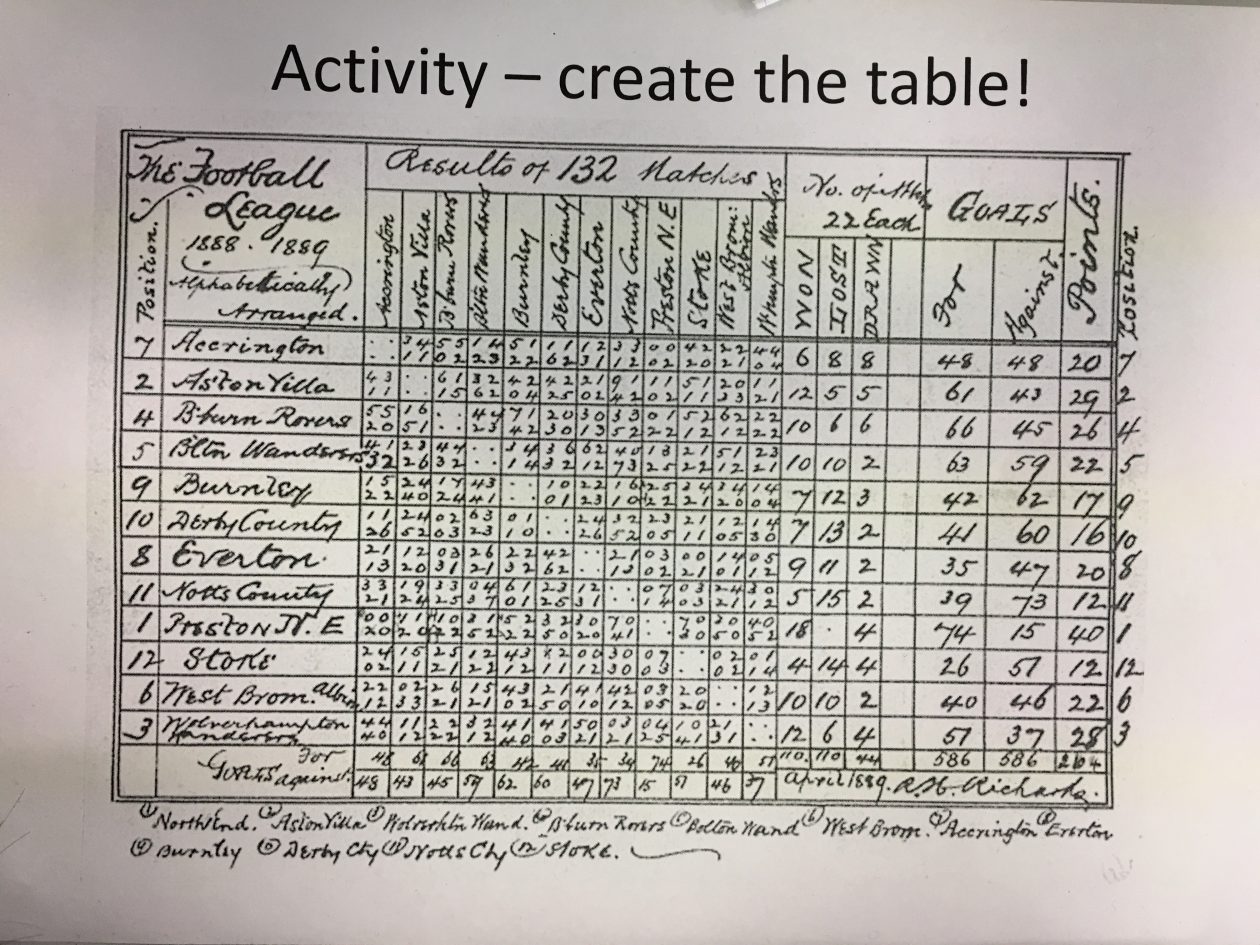
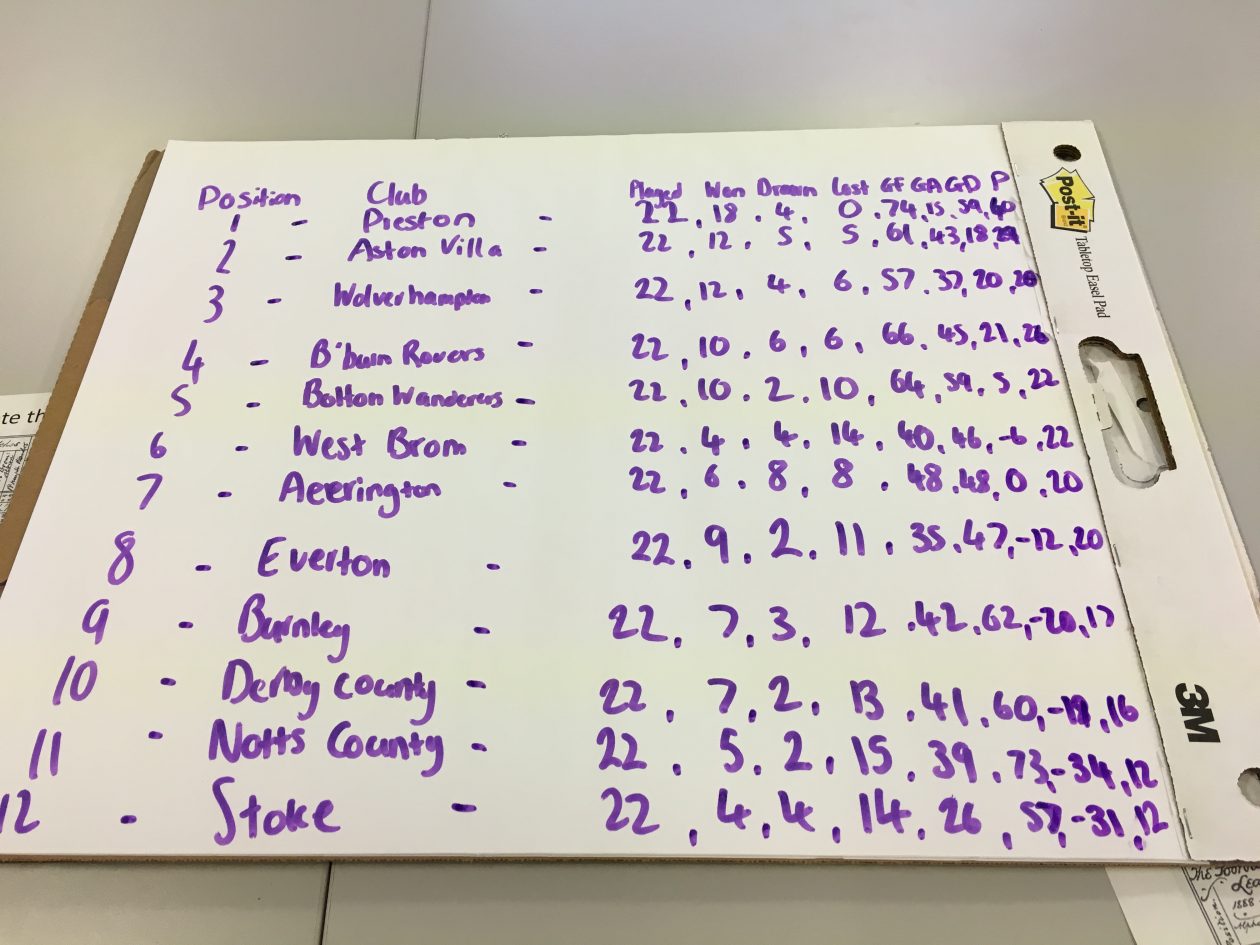 We decided to order the football clubs from top to bottom according to the most points a club had won. We used basic mathematical principles (Ma. 2010, p. 104) of counting to find out how many games each team had won, drawn or lost. To work out the goal difference we used the basic mathematical concept of subtraction, subtracting the goals against from goals for.
We decided to order the football clubs from top to bottom according to the most points a club had won. We used basic mathematical principles (Ma. 2010, p. 104) of counting to find out how many games each team had won, drawn or lost. To work out the goal difference we used the basic mathematical concept of subtraction, subtracting the goals against from goals for. Next, we designed our own sports game and looked at how maths was applied to the sport. Our sport was called Smack-ball. It was based on the memory of a game many people have played. This being, when you have a balloon you try and keep the balloon up in the air by hitting the balloon as it comes back down and you can’t let it touch the ground. So, essentially, smack-ball involves using a ball that is the size of your hand-span and it weighs 196 grams. The court will be rectangular, 10m by 5m, the shorter walls are the goals, there are three players on each team and the game lasts 10 minutes. The aim is to try and smack the ball (involving passes to your other team members) towards your teams wall without letting the opposite team intercept the ball.
Next, we designed our own sports game and looked at how maths was applied to the sport. Our sport was called Smack-ball. It was based on the memory of a game many people have played. This being, when you have a balloon you try and keep the balloon up in the air by hitting the balloon as it comes back down and you can’t let it touch the ground. So, essentially, smack-ball involves using a ball that is the size of your hand-span and it weighs 196 grams. The court will be rectangular, 10m by 5m, the shorter walls are the goals, there are three players on each team and the game lasts 10 minutes. The aim is to try and smack the ball (involving passes to your other team members) towards your teams wall without letting the opposite team intercept the ball.