Chance and probability link to the basic ideas or concepts of mathematics (Ma, 2010, p. 104). The basic understanding of probability is that it is the “[L]ikelihood or chance that something will happen.” (Tuner, no date, p.5). The “Probability of an event happening = Number of ways it can happen over the total number of outcomes.” (Probability, 2014). For example, when obtaining a two when rolling one dice, there are 6 outcomes possible. I can only get the two on the dice by landing on the two therefore, the probability is 1 out of 6. In this blog post, I am going to look at how probability can affect business and I am going to explore the links between gambling, social media likes, addiction and mathematics.
In our workshop, we looked at the different combinations possible when ordering meals (Holme, 2017). The fundamental maths is that there are multiple perspectives (various ways) to figure out the number of choices that could be made (Ma, 2010, p. 104). McDonald’s became a big business because they had a small variety of options on their menu. These options could all be cooked in a similar way and could be cooked fast. However, at one point, it was said that the McDonald’s menu was getting too big, which caused a decline in business. With more options available, there were complaints that the fast food restaurant, was not fast enough! Therefore, the less choice there is the more customers and sales. (Lutz, 2014). Restaurants could look into the probability of more choice vs the number of customers.
Gambling
Gambling in the UK is now at two billion pounds. However, gambling is addictive and produces a moral and an ethical issue. Addiction to gambling has led some people to steal due to the amount of debt they are in. The number of gambling addicts have doubled in six years and MPs aim to reduce this. It could have a knock-on impact on economy especially if many people are entering debt and Gambling is increasingly prevalent (as it can even be played at home now) (Gallagher, 2013).
Skinner did research on training people with rewards, this being the variable ratio schedule. Skinner suggests that we should not give rewards every time but to give them at random, to change up when we give a reward. He states that to train someone, we should keep rewarding them at the start which gets them hooked, then vary when the reward is given once the behaviour has been established. Casinos have researched this about rewards and in turn have used this information to get people to play and to keep them hooked (Weinschenk, 2013).
Rewards link to social media notifications such as emails or Twitter. We do not continually access these because we have got a notification or because we have a message but because we might have one, it’s the unpredictability. There is a potential reward. This is why we get addicted (Burkeman, 2011). I know I have opened my social media apps, knowing that sometimes a notification doesn’t pop up on my home screen but if I go into the app there is a possibility or a chance that I might get one if I open it. Therefore, this theory about rewards by Skinner can be applied to slot machines because if they rewarded someone every time they played, people wouldn’t get addicted. So, in order to get people addicted or hooked they vary when the rewards are given.
Teacher note: Could we use this idea or concept of varied rewards to have more positive behaviour in the classroom? This is something I would like to look into to develop my understanding of fundamental mathematics in the future.
Click here to watch a video on addiction to instagram likes. (Yates, 2017)
A reward such as a like on your Instagram causes a release of a chemical called dopamine. This gives us a ‘high’ which encourages our addiction to the likes further. We want more likes and we watch them roll in, creating an addiction because we like that feeling of satisfaction (How the Brain Gets Addicted to Gambling, 2017).
This theory of random rewards causing addiction, connects to the concept of randomness which is explored in the basic mathematical concept of probability and chance. Randomness according to De Finetti (1990, cited in Turner, no date, p. 3) is defined as an individual will not know what a result will be. However, can we determine what the outcome will be using the mathematical concept of probability? Therefore, if the outcome could be more predictable could this mean a reduced likelihood of addiction since it’s the unpredictability of rewards that gets us addicted (Burkeman, 2011).
Gambling relies on randomness and probability (Turner, no date, p. 3). However, it seems that we humans have a different view to randomness since we expect a random outcome to not have the same result in a row, when tossing a coin for example (Holme, 2017).

I thought that a random result wouldn’t have so many tails or heads in a row. When predicting, I tried to mix it up the result, I varied it to make the outcome what I thought to be random. Therefore, supporting the “Naïve Concept of Random Events” as I didn’t think the outcome would be in clumps (Turner, no date, p. 4). Thinking along the lines of, if this result hasn’t occurred much or at all, it’s going to next time. I did not expect a pattern (Turner, no date, p. 5). Even Apple had to make the random shuffle option for selecting songs, less random in order for it to seem more random to humans as the songs ended up being clustered (Bellos, 2010).
Therefore, it’s interesting that Howard (2013, cited in Smart Luck, 2017) contradicts that random outcomes can be in patterns even though the coins toss has just proven that there can be patterns in randomness. One tip that he recommends people use to win the lottery is to follow the human thinking of randomness. Meaning that you should not pick numbers that have a pattern or consecutive numbers. He also suggests that numbers shouldn’t be picked from the same group as its unlikely you’ll win. Although, this would contradict Apples random shuffle option, which often picked songs from the same album (same group) (Bellos, 2010). Furthermore, even though through analysing patterns, he has concluded that, “That which is most possible happens most often. That which is least possible happens least often.” However, the challenge with using probability to help you win in the lottery, is that it isn’t certain that it will occur (Probability, 2014).
This concept of randomness needs to be addressed in school to remove the misconception about randomness. Doing experiments such as the coin toss would be a great example for the class to see as it demonstrates a real-life example of randomness in probability such as the one shown below which we did in a workshop.
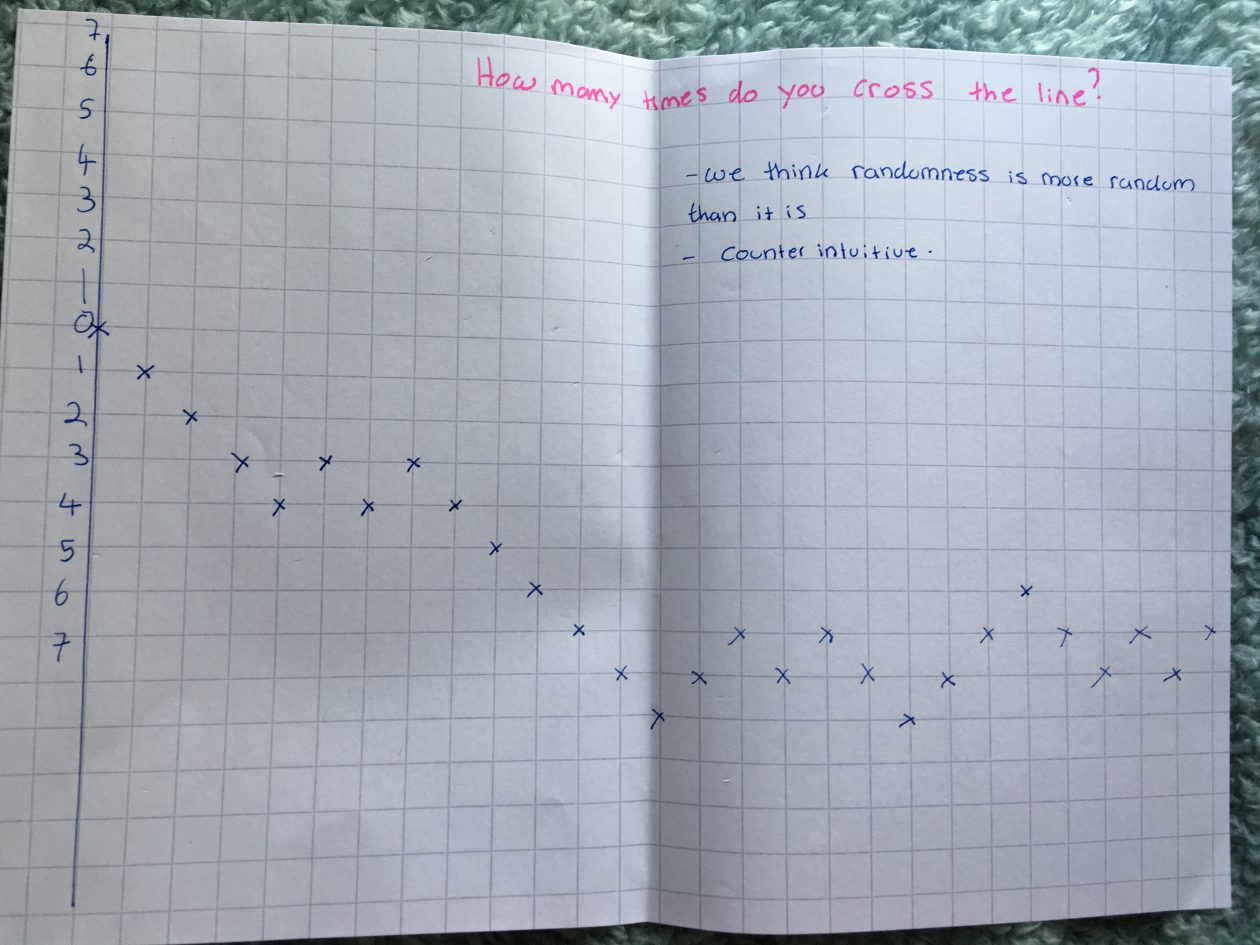
Regarding the point I made earlier about addiction being removed or reduced when gambling if the outcome is more predictable, this could be done by utilizing fundamental maths and probability. One example of this is by Darren Brown, who tried to estimate the speed of moving objects, looked at velocity and rate, using mathematics and engineering to guess where the ball might land on the roulette table (Bob, 2009). This being an example of different areas of maths connecting to others to solve a problem (Ma, 2010, p.104). However, even though he used all his knowledge and connected it together, he still was one out from being correct and winning. Similar to probability, it is only a “guide”, it isn’t certain that what is probable will occur (Probability, 2014).
In summary, probability could be used to help restaurants such as fast food places to work out the likelihood of how many customers they will have if they have a certain amount of options on their menu. Additionally, gambling is addictive because people love the satisfaction of the unpredictable rewards, the possibility of getting rewards which is similar to social media likes (Burkeman, 2011). Therefore, gambling machines would need to give rewards at random to keep people hooked which links to the basic concept of probability and chance in maths (Weinschenk, 2013). However, surprisingly there are patterns seen in randomness that humans do not expect. Furthermore, I explored how there is potential to reduce the addiction if the outcomes could be predicted using probability, chance and other areas of maths that could connect (Ma, 2010, p.104). Although, it seems that because probability cannot give an exact answer of the outcomes, its unreliable to use in this case (Probability, 2014).
List of references:
Bellos, A. (2010) ‘And now for something completely random, by Alex Bellos’, The Daily Mail, 7 December. Available at: http://www.dailymail.co.uk/home/moslive/article-1334712/Humans-concept-randomness-hard-understand.html (Accessed: 12 October 2017).
Bob (2009) Derren Brown: How to Beat a Casino. Available at: https://learningonscreen.ac.uk/ondemand/index.php/prog/011B9829?bcast=34497126 (Accessed: 12 October 2017).
Burkeman, O. (2011) ‘Can ‘intermittent variable rewards’ help you become addicted to more positive behaviours?’, The Guardian, 23 April. Available at: https://www.theguardian.com/lifeandstyle/2011/apr/23/this-column-change-life-random-rewards (Accessed: 12 October 2017).
Gallagher, P. (2013) ‘Addiction soars as online gambling hits £2bn mark’, Independent, 27 January. Available at: http://www.independent.co.uk/news/uk/home-news/addiction-soars-as-online-gambling-hits-2bn-mark-8468376.html (Accessed: 12 October 2017).
Holme, R. (2017) ‘Chance & probability’ [PowerPoint presentation]. ED21006: Discovering Mathematics (Year 2) (17/18) Available at: https://my.dundee.ac.uk/webapps/blackboard/execute/displayLearningUnit?course_id=_56905_1&content_id=_4941456_1 (Accessed: 12 October 2017).
How the Brain Gets Addicted to Gambling (2017). Available at: https://www.scientificamerican.com/article/how-the-brain-gets-addicted-to-gambling/ (Accessed: 12 October 2017).
Lutz, A. (2014) McDonald’s Menu Is Completely Out Of Control. Available at: http://uk.businessinsider.com/mcdonalds-menu-is-too-large-2014-12?r=US&IR=T (Accessed: 12 October 2017).
Ma, L., (2010) Knowing and teaching elementary mathematics (Anniversary Ed.)New York: Routledge.
Probability (2014) Available at: http://www.mathsisfun.com/data/probability.html (Accessed: 12 October 2017).
Smart Luck (2017) United Kingdom National Lottery Suggestion. Available at: http://www.smartluck.com/free-lottery-tips/england-nationallotto-659.htm (Accessed: 12 October 2017).
Tuner, N. (no date) Probability, Random Events, and the Mathematics of
Gambling. Available at: https://www.problemgambling.ca/EN/Documents/HPG%20Probabilty%20Final.pdf (Accessed: 12 October 2017).
Weinschenk, S. (2013) Use Unpredictable Rewards To Keep Behavior Going. Available at: https://www.psychologytoday.com/blog/brain-wise/201311/use-unpredictable-rewards-keep-behavior-going (Accessed: 12 October 2017).
Yates, E. (2017) What happens to your brain when you get a like on Instagram. Available at: http://uk.businessinsider.com/what-happens-to-your-brain-like-instagram-dopamine-2017-3 (Accessed: 12 October 2017).

