The Fibonacci Sequence is a fairly new concept to me, having only seen a flash of the term in a textbook during my MA1 school placement. The Discovering Maths module is responsible for properly introducing me to this concept, however it was a shock to learn that in reality, this peculiar set of numerals have been very much right in front of me all my life.
In a TED talk, Arthur Benjamin emphasises my shared belief that the vast majority of mathematics taught in education is primarily surrounds solving calculations with countless rules, often labelled as having one correct answer – especially in comparison to other fields such as English, where more flexible and diverse answers can be accepted (2013). Benjamin accentuates that more time should be spent on application of maths, and that it is both more interesting and enjoyable if we allowed ourselves to go beyond the HOW, and contemplate the WHY. The Fibonacci Sequence is a perfect example for this.
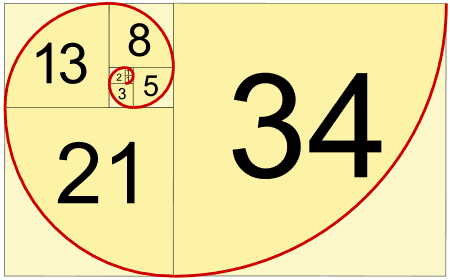
The idea of the Fibonacci Sequence is fairly simple. You take the first two numbers (0 and 1) and add them together to calculate the next digit – in this case, 1. This is followed by adding the new value with the previous – in this case, 1 and 1 to make 2, and so on. The image below lists the first set of numbers in the sequence.

There we have our calculation – and a pretty basic one at that. However, to perpetuate Benjamin’s statements, mathematics does not have to be a stale pattern of addition – it can be astonishingly magnificent, relevant and beautiful (Erikson, 2011).
To discover this, we link this set of numbers to the concept of ‘Ratio’. A ratio can be described as how much of one thing there is compared to something else. (Haylock, 2006). In regards to having a ‘perfect ratio’ where two things are perfectly proportioned, this value would emerge as 1.618034. The image below explains the method of obtaining this value.
When we put these two mechanisms together, we are able to uncover a startling connection. It has been proven that the further along to Fibonacci Sequence we travel, the closer the resulting ratio between two consecutive numbers is to the Golden Ratio (Boaler, 2009).
For example, 13/8 = 1.625
Much further along, we can divide 4181/2584 to obtain 1.618034!
The link between the Fibonacci Sequence and the Golden Ratio is abundant – however humans have yet to figure out what it is. Whilst I personally have no hope or intention of uncovering the meaning of this relationship, I am able to come to a personal conclusion as to whether or not this is all just a coincidence or if there are greater forces at play.
Many famous landmarks such as the Taj Mahal and Notre Dame have been labelled as having the ‘Golden Ratio’. Unfortunately, the age of these constructions mean we aren’t even sure if this was an intentional decision (Strange Mysteries, 2017). Could the Fibonacci sequence just be something we are naturally attracted to, and is it only limited to human beings?

Thanks to the nature, we can safely say the answer is no… at least to the latter question. Perhaps we are just naturally attracted by these numbers, yet man-made structures are not the only things that have the Golden Ratio present (Boaler, 2009). The image of the shell below conveys the lines clearly as the sequence increases into an elegant curve.

Much like the supposed mathematical construction decisions surrounding the Taj Mahal, but far more philosophical in depth, we currently don’t know and probably will never have concrete evidence on how our universe was created – just a possible evolved understanding of it (Francis, 2013). But the abundance of the Fibonacci sequence makes it very difficult to accept that this is all a coincidence. If the buildings and shells do not provide enough confirmation, we need only look at other natural examples that humans could not possibly interfere with – whether that be hurricanes/storms, flower petals, or indeed our own body. 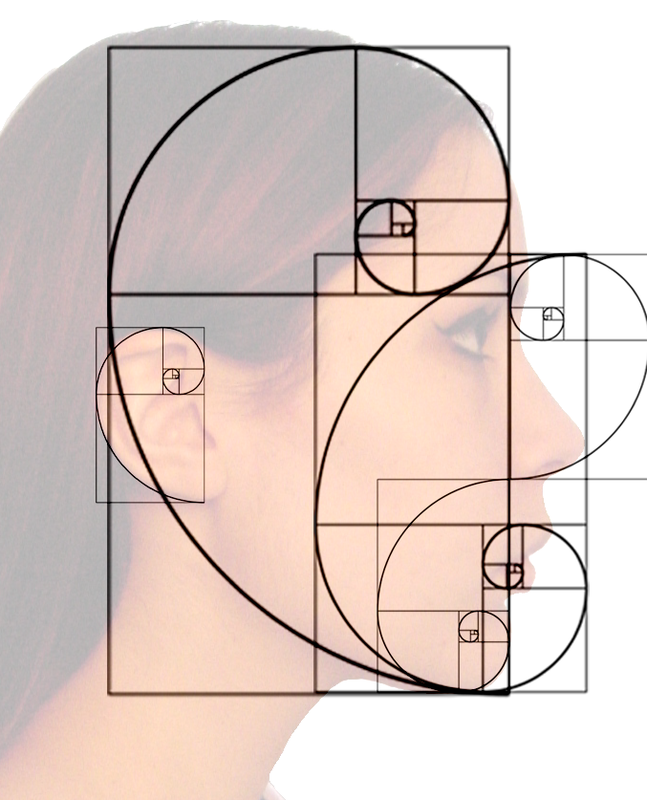
References
Boaler, J. (2009) The Elephant in the Classroom: Helping Children to Learn and Love Maths. London: Souvenir Press Ltd.
Erickson, M. (2011) Beautiful mathematics, Washington, D.C.: Mathematical Association of America.
Francis, M (2013) Will we ever… know what happened before the big bang? Available at: http://www.bbc.com/future/story/20130502-what-came-before-the-big-bang (Accessed: 9th October 2018)
Haylock, D. (2006) Mathematics explained for primary teachers. London: SAGE.
Strange Mysteries (2017) Why is 1.618034 So Important? Available at: https://www.youtube.com/watch?v=keLN89CWZ-A (Accessed: 9th October 2018)
TED (2013) The magic of Fibonacci numbers | Arthur Benjamin. Available at: https://www.youtube.com/watch?v=SjSHVDfXHQ4&t=287s (Accessed: 9th October 2018)
Images Used
https://www.pinterest.co.uk/pin/500181102340885176/?lp=true
https://www.quora.com/What-is-so-special-about-the-golden-ratio
https://www.phimatrix.com/architectural-design-golden-ratio/
https://www.theodysseyonline.com/7-beautiful-examples-fibonacci-sequence-nature
