In this vlog post, I have discussed how this module has inspired me to become more confident in my ability and how the IBSE approach is beneficial in learning science.
Category Archives: 3.1 Teaching & Learning
Curiosity in Science
This is all about curiosity and why it is important to promote curiosity amongst children.
Oil+Water+Washing up Liquid+ Vitamin C Tablets = Lava lamp?!
A Reflection of an Electricty lesson with a Primary 7 Class
At the beginning of this module, I was very weary of teaching science because it is something that I have done in the past with little success. This was because I did not possess the confidence needed to teach science efficiently in the primary school. In hindsight, this module has allowed myself as a developing practitioner to feel more confident in my ability, especially with regards to inquiry based learning and allowing children to explore different issues and aspects of science. Luckily, this module has given me the opportunity to teach two different age groups in science which is the reason for this blog/vlog post. The first lesson was do with acids and alkalis with a primary six class and the second lesson was to do with electricity with a primary 7 class. This post today aims to describe what my colleagues did to exemplify inquiry based learning and the vlog post will reflect on the experience.
The activity was based around the issue of cars and their headlights. Our ‘hook’ displayed numerous cars (old and new) with their headlights on. The children were asked to discuss the function of headlights and why cars need them. Once the children discussed and answered these questions, the children were asked to think about how the car headlights get their power and were asked to discuss. this matter. To highlight to the children how this happens, we lined them up outside the classroom and asked the to think about how electricity runs through wires. Questions were along the lines of ‘when we flick a light switch, does the light come on fast or slow? The children then passed along the line to symbolise how electricity runs from a batter to a lightbulb. One of us walked alongside the children to symbolise that electricity is passed along from atom to atom.
Once the ball analogy concluded, the children were involved in making their own circuits, comparing things such as:
one battery connected to one lightbulb
Two batteries connected to one lightbulb.
Two batteries connected to two lightbulbs.
However, before this we talked about hypothesising and why it is important in science. Children then created their own hypotheses about what would happen with the above scenarios. The interesting thing was that hypotheses varied from child to child showing how individualistic children are when it comes to their own ideas. Each adult that was involved in the activity acted as a facilitator to the children’s’ learning, which emphasised the need for social constructivism in science. Once the children completed their circuits, we had a general plenary on the things the have learned and to see if they enjoyed the activity.
Below is the link to my professional reflection on the activity focussing on what went well during the lesson, what could be improved upon and how the children interacted with the lesson.
Looking at Science Through Hurricanes
In MA2 I wrote a blog post called ‘the maths behind hurricane Abigail’ which identifies how hurricanes relate to mathematics through the Fibonacci sequence. Fast forward to MA4 and it is still something that I am particularly interested in. In my future career, I wish to incorporate a topic based around hurricanes and natural disasters through topical science. This has inspired me to compose a vlog post to highlight in what ways this can be taught in the classroom. The Scottish Government (2010) highlight that children will gain the benefits from science by promoting relevance in their learning. To address this, the vlog post identifies how using active and inquiry based experiences can allow children to see the benefit of learning about hurricanes and natural disasters. This has identified to myself as a science learner that science is not just about conducting experiments and constructing graphs (Shamsudin, Abdullah, and Yaamat, 2013). Instead, it has highlighted that an incredible amount of thinking and asking questions is necessary to establish how the world works.
Please visit the link below to look at my vlog post.
https://www.youtube.com/watch?v=Xf8vybYsioU
References
Scottish Government. (2010) Curriculum for Excellence: Science Principles and Practices. Available: https://education.gov.scot/Documents/sciences-pp.pdf. Last Accessed: 24/10/17.
Shamsudin, N., Abdullah, N., and Yaamat, N. (2013) ‘Strategies of Teaching Science Using an Inquiry based Science Education (IBSE) by Novice Chemistry Teachers.’ Procedia – Social and Behavioural Sciences. 90(1): Pp 583-592.
Christmas in Mathematics – ideas for the classroom
Its that time of year again when the lights are up, songs are being sung, decorations are being hung and joy is absolutely everywhere. What is this time you ask? it is indeed Christmas. It is obvious that Christmas is a time for giving and thinking of loved ones, but after a recent blog post from Andy Hughes (titled ‘Christmaths’), I have been inspired to blog about how maths can be incorporated into Christmas in fun and inventive ways. In addition, it has made me want to uncover the fundamental principles of mathematics in Christmas.
Hughes (2015) in his blog post ‘Christmaths’ describes mathematics in Christmas. He states that snowflake’s are a ‘fractal (a fractal is a shape that contains similar patterns which recur throughout the shape on a smaller scale)’. In addition he identifies that zooming in on a snowflake just produces more details and can splurge up fundamental processes such as scaling, shape and ratio – very fundamental processes. On a larger scale, lets take the fundamental process of shape. As I have mentioned numerous times before, maths is all around us. In a seasonal sense, we only need to look at our Christmas trees to see that shape is evident. For example, Christmas baubles. These are spherical in shape. The star on top of the tree also shines bright, but is still a shape. However, what is the maths behind a Christmas tree? It could be suggested that there is maths in assembling a Christmas tree (especially and artificial one. For example, you will need to have the right length of Christmas tinsel to pass around the tree – the mathematical concept of length and measurement. In addition, you will need to have enough Christmas baubles in order for the tree to be symmetrical. Talking about symmetry, this can be used widely as examples to help children understand this concept. For example, trees are symmetrical, as are snowmen, stars, snowflakes.. the list goes on. This can be used as a consolidation activity and it effectively ties Christmas into mathematics.


Moreover, Christmas time in the classroom should be an exciting and engaging time for children. So why can’t we use maths within Christmas? Even if it is not directly from a maths lesson. Board games are a fantastic way to do this and they challenge a range of mathematical concepts. Take monopoly, for example. Now, I am not going to lecture you on how to play monopoly as I am sure we all have a ‘profound understanding’ of how to play it. However, what does monopoly all boil down to? Money. In order to play this game, children must have a basic knowledge of money and will have to subtract or add together money when they land on someone’s property or even if they pass go! I find this to be pretty incredible – its fun and engaging, but you are learning at the same time… Do you see where I am going with this? Take snakes and ladders – counting is the fundamental principle there. Cluedo – problem solving to find out who really committed the crime. Even in dominos there is a basic element of counting. Probability is also another fundamental principle that can be seen in games that use dice – what is the probability of landing on a six? Lets be honest, which games do not have dice in them?
It is obviously apparent that maths is incorporated into Christmas profoundly. If you even think about presents under your tree – some are cuboidal and some are spherical. Shape is such a common theme within Christmas. So when your opening your presents this year, have a second thought about how maths is incorporated into Christmas – it may even inspire you to write a blog post!!!!

reference:
Hughes, A. (2015) Christmaths. In a Class of my Own. Last accessed 06/12/15. Available at https://blogs.glowscotland.org.uk/glowblogs/ajhportfolio/2015/12/02/christmaths/
Beautiful Mathematics – an Outdoor Perspective
When we think of mathematics, we often think numbers, formulas, data handling and a whole host of other mathematical concepts. However, have you ever just looked around you whilst out in the outdoors and thought ‘maths is beautiful?” I guess its a thought that never springs to mind. However, mathematics is actually in everything we see in the outdoors (believe it or not) and this blog post aims to highlight how beautiful maths is within the context of the outdoors.
To see mathematics in the outdoors, we do not need to look far. It is in the very buildings that you see walking up and down the street. Here is a building that should all be too familiar:
For those of you who don’t know, this is the Dalhousie Building at Dundee University. I don’t know about you, but I feel believe that this is an architectural masterpiece. Firstly, if you look at the design, it is very visually appealing and it incorporates squares and curves to create a building that is grand in size. Where does the maths come into this? Well if we think back the original plans of the building, it had to be measured accurately in order for it to come together. Of course, there would have been slight room for error, but it had to be pretty accurate. If we think about the windows, the architects had to create enough space so they can tessellate perfectly. This absolutely astounds me. When looking back to a lecture on the golden ratio, you can almost see it happening here. To elaborate, the golden ratio was a ratio used since the 1500’s as it was perceived to be aesthetically pleasing. It uses the formula:

This can be best described using this square:

Basically, A golden rectangle (in pink) with longer side a and shorter side b, when placed adjacent to a square with sides of length a, will produce a similar golden rectangle with longer side a + b and shorter side a. This illustrates the relationship 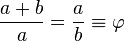 .
.
This all together makes this pattern which can be recognised in Fibonacci’s sequence:

This is seen to make an aesthetically appealing design:
 Picture Courtesy of apple.
Picture Courtesy of apple.
So where does our Dalhousie building come into this? Well if we look at the elevation of the building (the front of building consisting with the front entrance and the classrooms in the second block, we get a (block two) and b the entrance which would create this perfect spiral. I find this absolutely intriguing. This is not just the case for Dalhousie, However, this is the case for most things in our world. If we look at this plant:

we can see the golden ratio coming into play along with Fibonacci’s sequences. This officially ties nature and mathematics together and the results are absolutely breath taking. In this image above, not one segment of the flower is out of place. They all spiral in the same direction towards the centre of flower which makes it symmetrical.

And here it is again (sorry, I couldn’t resist). Everything in this world is tied into mathematics and this is why maths is beautiful. Whether its looking at buildings or looking at flowers, the fundamental mathematics is there. With buildings, its all do with measuring and being precise and I guess with flowers you could say pattern. Whatever the outcome, just have a look at the world around you and it might amaze you like it has me. Maths is beautiful.
Mathematics in Demand Planning – Show me the Money!!!!
As mentioned in my previous blog posts, mathematics is incorporated in to absolutely everything in life. This idea was further embedded during a lecture on supply chain and logistics in maths. It was a three hour input, but It was honestly the best maths class to date. It was completely relevant, interactive and so much fun. This blog post aims to draw on points about fundamental mathematics on previous blog posts and how it is incorporated into demand planning.
Firstly, when we talk about supply chain and logistic planning, what springs to mind is food. Apart from the odd rumble of my stomach, there is actually some mathematical concept behind this all. lets take crisps for example. If we think about the bar code, it has a significant amount of numbers around it (see image below).
Within the red circle, is a best before date 06/11/10. The number to the side says 06:51 which would highlight the time where the big packet (if it is a multipack) was closed. The number code under 06:51 is 275 which means which day within the year it has been produced. These timings are absolutely crucial for the company to give an accurate sell by date which will prevent their customers from getting food poisoning. The fundamental mathematics behind this is predicting by using the numbers to provide an accurate time scale for consumption. To an extent, the fundamental mathematics behind it could be knowing the date and the days of the year. Furthermore, each packet of crisp has a certain weight which could identify that another aspect of fundamental mathematics is weight. Even when the small packets are being placed into the big multi-pack bag, there are still a specific number which is out in each bag. This takes the art of crisp making and manufacturing down to being able to count. Fundamentally, that is astounding. Come to think about it, think of all the activities that you could bring in to the classroom around crisps. Potentially you could go down the rout of how the crisps are made, what machinery is used to manufacture crisps and how they are programmed.. you could even take a stab at making your own crisps!! Of course, maths comes into every single one of those activities.
However, enough about crisps… the thought of them makes me hungry. To continue this idea of supply chain and logistics, we must talk about food miles (I am aware that I am talking about food again). A prime example of this is when Richard (our lecturer) had a job in Trinidad and Tobago where he worked with a logistic company which was responsible for transferring food around the island , and the tiny islands within the outer Hebrides. He spoke fondly a man who would work out the routs to take in order for the items to be delivered. This seems to be pretty straight forward… However, you would be wrong to think that. This man used to do all this through his head. It was therefore absolutely crucial that he was able to know the routs expertly, he would have to know how much petrol he would need for the lorry, he would have to know if the lorry needed to be transported onto a ferry in order to deliver. Where is the maths you ask? Well it all comes down to money. This man was able to work out how much money it would roughly cost him and the he was able to calculate how much profit he was going to make. It is very clear that this man had a PUFM in the sense that he was able to estimate the rout and how much money it was going to cost him. Not only this, he had to be able to pack the lorry in the most proficient was possible (i.e a poorly packed lorry is the difference between making two trips or one trip). Therefore, he would pack the lorry in a way that used tessellation. making sure all the boxes (or items) were able to be pieced together. I find this to be absolutely fascinating because the basic mathematical principles is in an actual concept which mathematics is so important. What I find more intriguing is that this gentleman was able to do it all in his head -I take my hat off to you sir!! In addition cargo hold, it all boils down to profit and money. This is why companies will ensure that all their stock is being transported all at once. For example (see image below) This boat is made up cargo containers which are cuboidal. They can all tessellate together in order to take more stock to and from places at once – fascinating!! To find out ore on my thoughts on tessellation, please visit my blog post “Active Learning in Mathematics.”

Now in terms of demand planning, we were able to have a go with this ourselves. We had to form a team and we had a staring budget of £5000. We had to buy stock through different dates of the year (June to august, for example). We had a list of items that we could buy and sell on for a profit. We had to estimate (depending on the time of year) which stock that would potentially sell. The mathematics behind it was simple, but proved very tricky. Richard would tell us how the stock had sold in a percentage wise. We would then have to calculate the percentage of what we sold and carry on the remainder of what we didn’t sell. We would take our reading and then repeat this process again. It was probably the most fun I had every had in a maths lecture. There were so much fundamental mathematics that had to be addressed – such as money (spending to a budget and adding calculating the left overs by using a simple take away sum). In addition, the fundamental process of carrying over was quite tricky if you haven’t used it in a while. Furthermore, the use of simple percentages in working out how much money we had made was very interesting. HOWEVER, it has taken me up until now to realise that data handling is extremely important not just in mathematics, but also demand planning
I will say this again, ‘MATHS YOU HAVE AMAZED ME!!!’ in addition, you actually do this within the context of the class because I feel that this is so beneficial for children to understand and so they can continue there love for mathematics.
Maths in Astronomy
I was absolutely intrigued in today’s maths lecture about maths in astronomy. In my previous blog post, I argued that mathematics was apparent in every single thing on earth. However, after today, I realise that it goes beyond the earth into our universe. This blog aims to pick out the fundamental mathematics in space and how it can be applied to the classroom.
An important point about today’s lecture was the idea that there are millions upon millions of stars in our universe (approximately 10,000,000,000,000,000,000,000.) That idea completely sums up that the universe is a massive place. However, I am not blogging about the numbers and facts about space, but I am trying to delve in to the fundamental maths. A potential aspect of fundamental mathematics in space is potentially base systems. The fact that massive numbers are used to represent how far a planet is away from another or how big or the diameter of a certain planet is. Without the basic knowledge of numbers, this would not be possible to comprehend. In addition to this, take distance for example, to define how far away a particular object is, we use KM. Therefore, we have to have a basic knowledge of distance. For example, if we only used millimetres to measure distances, we would be there all day and it would cause some sort of confusion if you were to give someone directions.
Continuing on the idea of fundamental mathematics, the notion of light years was introduced and what excited me was that a light year is the distance light travels is one year. If we look up at the night sky and we see many bright and sparkling stars looking back at us. However, what is apparent is that those stars have probably imploded years ago. The closest star to us is four light years away. So basically if the star had imploded, we wouldn’t know until four years later. I find that concept fascinating and it highlights that space is huge. In addition to this, when looking at galaxies, I found Fibonacci’s sequence in amongst it all. You can see our milky way twisitng and spiralling to create a very beautiful scenery.
So how can this be introduced in the wider context? Or within the context of the classroom? Luckily, I have had some experience with this during my first year placement. What it was mostly concerned with was the idea of learning facts and figures, naming the planets, and making wall displays. I completely understand that this was the children’s topic work, but it would be so beneficial to apply mathematics to this topic, especially fundamental mathematics. Gaining a good knowledge of the solar systems is good, but we as teachers should be giving our children opportunities to explore the notion of maths in astronomy and play around with it. This would make for a much more interesting lesson and would probably be more beneficial than learning facts and figures. The ideal thing about mathematics is the idea that it can be playful and experimental and fundamental maths allows this due to bringing ideas back to basics and then building the learning up and up.
The Maths Behind Hurricane Abigail
After all this hype about a potentially menacing storm that has hit the shores of Scotland, I thought to myself that it couldn’t actually be that bad. I was, however, mistaken to this notion. After walking along Dundee City high street a few moments ago, I was soaked within an inch of my life. It was calm one minute, then BOOM chaos! The storm has now come to Dundee and as I look out my window now, Dundee has been disrupted with small amounts of damage to public billboards and bus shelters. This got me thinking about the intensity of a storm and how vast they can be. It also got me thinking about how the maths come in to part with storms. As I sit with a blanket over my lap and a cup of tea by my side, I am going to attempt to discover the fundamental maths behind a hurricane and why they can be incredibly frustrating for everyone.
In my last few blog posts, I have been concerned with talking about maths as an active subject through many things like tessellation and maths with stories and play. This blog post will be somewhat different to these, but the principles and the fundamental mathematics still apply. Firstly, a hurricane is a mass storm with a violent wind and reaches above a speed of 75 mph!! 75 miles per hour… I don’t know what is scarier, the damage that it causes or the notion that it can travel faster than the speed limit of a car on the motorway. According to NASA (undated), Hurricanes are like giant engines that use warm, moist air as fuel. That is why they form only over warm ocean waters near the equator. The warm, moist air over the ocean rises upward from near the surface. Because this air moves up and away from the surface, there is less air left near the surface. Another way to say the same thing is that the warm air rises, causing an area of lower air pressure below. NASA continue by suggesting that air from surrounding areas with higher air pressure pushes in to the low pressure area. Then that “new” air becomes warm and moist and rises, too. As the warm air continues to rise, the surrounding air swirls in to take its place. As the warmed, moist air rises and cools off, the water in the air forms clouds. The whole system of clouds and wind spins and grows, fed by the ocean’s heat and water evaporating from the surface. In addition, a hurricane has an abundance of cumulonimbus clouds that form circular bands. The fundamental mathematics of a hurricane is its circular formation. Not only this, it is astonishing the way that hurricanes actually rotate. Do they rotate clockwise, or anticlockwise? storms from the north of the equator spin anti-clockwise and storms below the equator spin clockwise. This is because the Earth rotates on its axis. I find that so absolutely fascinating to say the least. It ultimately highlights that Mathematics is incorporated into absolutely everything that we see in this world and I agree with Will Berry on that one after his lecture on maths in the outdoors.
So why does this leave me feeling fascinated? Well probably because I am thinking about the mathematical activities that you could do within the context of the classroom. Firstly, you could investigate and display the different levels a hurricane is classified as. See diagram below:
| Category | Wind Speed (mph) | Damage at Landfall | Storm Surge (feet) |
| 1 | 74-95 | Minimal | 4-5 |
| 2 | 96-110 | Moderate | 6-8 |
| 3 | 111-130 | Extensive | 9-12 |
| 4 | 131-155 | Extreme | 13-18 |
| 5 | Over 155 | Catastrophic | 19+ |
The children can ultimately collect the data to classify different (old or new storms) from around the world, especially in the case of hurricane Abigail. In addition, the children could also find the speed of the hurricane and predict how far it will travel and in what time by using the speed, distance, time formula. This is just naming a few, but please feel free to comment with any other activities that you can think of as I would like to read them.
Fundamentally, the basic maths behind an activity to do with a hurricane is research skills. Being able to tally, collect data and the general notion of handling and organising information. Not only this, this is good for children deepen their understanding of probability and likelihood of a storm like this happening again. The activities can be in abundance if you put your mind to it.
Finally, I will leave you with this satellite image of hurricane Abigail (picture taken by the University of Dundee):

This is a picture of hurricane Abigail just off the coast of North West Scotland. You can see the spiral motion and you can almost imagine the wind swishing and swaying around. What I find to be completely fascinating about this picture is that you can see Fibonacci’s sequence spiralling around and around (see image below):
 Mathematics… You have amazed me again.
Mathematics… You have amazed me again.



