Tag Archives: Fibonacci Sequence

Beautiful Mathematics – an Outdoor Perspective

When we think of mathematics, we often think numbers, formulas, data handling and a whole host of other mathematical concepts. However, have you ever just looked around you whilst out in the outdoors and thought ‘maths is beautiful?” I guess its a thought that never springs to mind. However, mathematics is actually in everything we see in the outdoors (believe it or not) and this blog post aims to highlight how beautiful maths is within the context of the outdoors.

To see mathematics in the outdoors, we do not need to look far. It is in the very buildings that you see walking up and down the street. Here is a building that should all be too familiar:

For those of you who don’t know, this is the Dalhousie Building at Dundee University. I don’t know about you, but I feel believe that this is an architectural masterpiece. Firstly, if you look at the design, it is very visually appealing and it incorporates squares and curves to create a building that is grand in size. Where does the maths come into this? Well if we think back the original plans of the building, it had to be measured accurately in order for it to come together. Of course, there would have been slight room for error, but it had to be pretty accurate. If we think about the windows, the architects had to create enough space so they can tessellate perfectly. This absolutely astounds me. When looking back to a lecture on the golden ratio, you can almost see it happening here. To elaborate, the golden ratio was a ratio used since the 1500’s as it was perceived to be aesthetically pleasing. It uses the formula:

$\frac{a+b}{a} = \frac{a}{b} \ \stackrel{\text{def}}{=}\ \varphi,$

This can be best described using this square:

Basically, A golden rectangle (in pink) with longer side a and shorter side b, when placed adjacent to a square with sides of length a, will produce a similar golden rectangle with longer side a + b and shorter side a. This illustrates the relationship 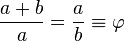$\frac{a+b}{a} = \frac{a}{b} \equiv \varphi$ .

This all together makes this pattern which can be recognised in Fibonacci’s sequence:

This is seen to make an aesthetically appealing design:

Picture Courtesy of apple.

So where does our Dalhousie building come into this? Well if we look at the elevation of the building (the front of building consisting with the front entrance and the classrooms in the second block, we get a (block two) and b the entrance which would create this perfect spiral. I find this absolutely intriguing. This is not just the case for Dalhousie, However, this is the case for most things in our world. If we look at this plant:

we can see the golden ratio coming into play along with Fibonacci’s sequences. This officially ties nature and mathematics together and the results are absolutely breath taking. In this image above, not one segment of the flower is out of place. They all spiral in the same direction towards the centre of flower which makes it symmetrical.

And here it is again (sorry, I couldn’t resist). Everything in this world is tied into mathematics and this is why maths is beautiful. Whether its looking at buildings or looking at flowers, the fundamental mathematics is there. With buildings, its all do with measuring and being precise and I guess with flowers you could say pattern. Whatever the outcome, just have a look at the world around you and it might amaze you like it has me. Maths is beautiful.

Maths in Astronomy

Leave a reply

I was absolutely intrigued in today’s maths lecture about maths in astronomy. In my previous blog post, I argued that mathematics was apparent in every single thing on earth. However, after today, I realise that it goes beyond the earth into our universe. This blog aims to pick out the fundamental mathematics in space and how it can be applied to the classroom.

An important point about today’s lecture was the idea that there are millions upon millions of stars in our universe (approximately 10,000,000,000,000,000,000,000.) That idea completely sums up that the universe is a massive place. However, I am not blogging about the numbers and facts about space, but I am trying to delve in to the fundamental maths. A potential aspect of fundamental mathematics in space is potentially base systems. The fact that massive numbers are used to represent how far a planet is away from another or how big or the diameter of a certain planet is. Without the basic knowledge of numbers, this would not be possible to comprehend. In addition to this, take distance for example, to define how far away a particular object is, we use KM. Therefore, we have to have a basic knowledge of distance. For example, if we only used millimetres to measure distances, we would be there all day and it would cause some sort of confusion if you were to give someone directions.

Continuing on the idea of fundamental mathematics, the notion of light years was introduced and what excited me was that a light year is the distance light travels is one year. If we look up at the night sky and we see many bright and sparkling stars looking back at us. However, what is apparent is that those stars have probably imploded years ago. The closest star to us is four light years away. So basically if the star had imploded, we wouldn’t know until four years later. I find that concept fascinating and it highlights that space is huge. In addition to this, when looking at galaxies, I found Fibonacci’s sequence in amongst it all. You can see our milky way twisitng and spiralling to create a very beautiful scenery.

So how can this be introduced in the wider context? Or within the context of the classroom? Luckily, I have had some experience with this during my first year placement. What it was mostly concerned with was the idea of learning facts and figures, naming the planets, and making wall displays. I completely understand that this was the children’s topic work, but it would be so beneficial to apply mathematics to this topic, especially fundamental mathematics. Gaining a good knowledge of the solar systems is good, but we as teachers should be giving our children opportunities to explore the notion of maths in astronomy and play around with it. This would make for a much more interesting lesson and would probably be more beneficial than learning facts and figures. The ideal thing about mathematics is the idea that it can be playful and experimental and fundamental maths allows this due to bringing ideas back to basics and then building the learning up and up.

The Maths Behind Hurricane Abigail

2 Replies

After all this hype about a potentially menacing storm that has hit the shores of Scotland, I thought to myself that it couldn’t actually be that bad. I was, however, mistaken to this notion. After walking along Dundee City high street a few moments ago, I was soaked within an inch of my life. It was calm one minute, then BOOM chaos! The storm has now come to Dundee and as I look out my window now, Dundee has been disrupted with small amounts of damage to public billboards and bus shelters. This got me thinking about the intensity of a storm and how vast they can be. It also got me thinking about how the maths come in to part with storms. As I sit with a blanket over my lap and a cup of tea by my side, I am going to attempt to discover the fundamental maths behind a hurricane and why they can be incredibly frustrating for everyone.

In my last few blog posts, I have been concerned with talking about maths as an active subject through many things like tessellation and maths with stories and play. This blog post will be somewhat different to these, but the principles and the fundamental mathematics still apply. Firstly, a hurricane is a mass storm with a violent wind and reaches above a speed of 75 mph!! 75 miles per hour… I don’t know what is scarier, the damage that it causes or the notion that it can travel faster than the speed limit of a car on the motorway. According to NASA (undated), Hurricanes are like giant engines that use warm, moist air as fuel. That is why they form only over warm ocean waters near the equator. The warm, moist air over the ocean rises upward from near the surface. Because this air moves up and away from the surface, there is less air left near the surface. Another way to say the same thing is that the warm air rises, causing an area of lower air pressure below. NASA continue by suggesting that air from surrounding areas with higher air pressure pushes in to the low pressure area. Then that “new” air becomes warm and moist and rises, too. As the warm air continues to rise, the surrounding air swirls in to take its place. As the warmed, moist air rises and cools off, the water in the air forms clouds. The whole system of clouds and wind spins and grows, fed by the ocean’s heat and water evaporating from the surface. In addition, a hurricane has an abundance of cumulonimbus clouds that form circular bands. The fundamental mathematics of a hurricane is its circular formation. Not only this, it is astonishing the way that hurricanes actually rotate. Do they rotate clockwise, or anticlockwise? storms from the north of the equator spin anti-clockwise and storms below the equator spin clockwise. This is because the Earth rotates on its axis. I find that so absolutely fascinating to say the least. It ultimately highlights that Mathematics is incorporated into absolutely everything that we see in this world and I agree with Will Berry on that one after his lecture on maths in the outdoors.

So why does this leave me feeling fascinated? Well probably because I am thinking about the mathematical activities that you could do within the context of the classroom. Firstly, you could investigate and display the different levels a hurricane is classified as. See diagram below:

Category	Wind Speed (mph)	Damage at Landfall	Storm Surge (feet)
1	74-95	Minimal	4-5
2	96-110	Moderate	6-8
3	111-130	Extensive	9-12
4	131-155	Extreme	13-18
5	Over 155	Catastrophic	19+

The children can ultimately collect the data to classify different (old or new storms) from around the world, especially in the case of hurricane Abigail. In addition, the children could also find the speed of the hurricane and predict how far it will travel and in what time by using the speed, distance, time formula. This is just naming a few, but please feel free to comment with any other activities that you can think of as I would like to read them.

Fundamentally, the basic maths behind an activity to do with a hurricane is research skills. Being able to tally, collect data and the general notion of handling and organising information. Not only this, this is good for children deepen their understanding of probability and likelihood of a storm like this happening again. The activities can be in abundance if you put your mind to it.

Finally, I will leave you with this satellite image of hurricane Abigail (picture taken by the University of Dundee):

Storm Abigail

This is a picture of hurricane Abigail just off the coast of North West Scotland. You can see the spiral motion and you can almost imagine the wind swishing and swaying around. What I find to be completely fascinating about this picture is that you can see Fibonacci’s sequence spiralling around and around (see image below):

Mathematics… You have amazed me again.