Art and artistic expression both have connotations of creativity, freedom and exploration for those that are deemed artistically imaginative to delve deep into their own vivid minds. One must be capable of thinking outside of the box of convention when viewing artwork, for example, to be appreciative of the emotions or message an artist is trying to convey.

Mathematics, on the other hand, follows formulae with the intentions of finding answers to problems… Doesn’t seem very creative, does it? Nor is it very thought provoking in terms of gaining a lasting emotion that viewing a controversial Banksy exhibit could produce, for example… I am digressing but one could argue that they’re more likely to be overwhelmed emotionally by maths than a painting…
Mathematics and Art don’t seem to go together quite so well do they?
A person that is seen as a creative being is less likely to be a ‘math person’ and be more likely to be a ‘free spirit’ who is in touch with the world. They do not feel the need to conform, right? Many of the great artists, such as El Greco, had this exact notion when being challenged by friends and family who thought of them as failures for taking up art as a profession. Free spirits break away from structure, order and routine that are upheld and followed rigorously by so many educators and scholars in the subject of Mathematics. Why?
Many people will agree that their math lessons at school did not involve any creative thinking, which, through recurring practices, disconnects the relationship between Art and Mathematics. This creates this societal view that a person can be naturally gifted in the arts or mathematics. Why not both?
Art and expression are the real world. Humans use art as a method to translate emotions (Mcniff, 2006). Creativity is not limited to artists, however. Across various industries and institutions people need to be innovative enough to conjure up ideas to tackle problems they are faced with in their profession and their everyday lives. So, mathematicians can be free spirits just like artists can be math people. A mathematician can be an artist just as an artist can do mathematics.
Any form of categorisation for determining the source of someone’s mathematical ability and their relationship with numbers is really a form of escapism from the real problem that people do not have profound enough knowledge of mathematics within the real world (Ma, 2010).
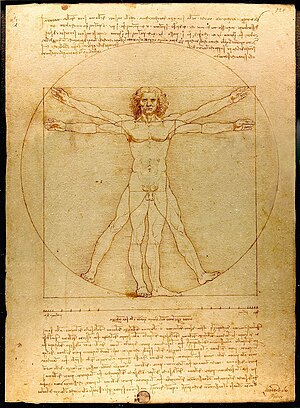
Da Vinci, Vitruvian Man (1490)
Leonardo da Vinci’s famous Vitruvian Man is a prime example of the everlasting marriage that Mathematics and Art have with each other. The piece depicts the dimensions of man in correlation to shape and symmetry. Both mathematically and artistically, the artwork shows that the ‘perfect human body’ is symmetrical in its measurements and dimensions, and da Vinci (and many others) argued that this was not by coincidence.
The Roman Architect and mathematician Vitruvius, who explored perfect proportions in building design and its connection with the human body, heavily inspired the Vitruvian man (hint is in the name, really) because his work led him to believe that we were the source of dimensions and that some higher power had granted us these tools for measurement. This was based upon the understanding that we were made up of symmetry.Two eyes that are near identical, two hand that have five fingers each and two feet that have five twos each being just a few examples.
Vitruvius used symmetry of the human form to aid his writing in various volumes of literature about architecture in Rome.
Another beauty of mathematics to behold is the golden ratio. The golden ratio was coined by the father of geometry, Euclid, and it is a number that is derived from taking a line and separating it into two in a manner that the ratio of the shortest segment to the longest is the same as the ratio of the longest to the original line (Bello, 2010).
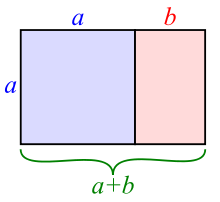
Golden Ratio Diagram
You end up with a ratio of 1.6180339887, which cannot be represented as a whole fraction, deeming it an irrational number. The Greeks called this phi.
“The Greeks were fascinated by phi. They discovered it in the five pointed star, or pentagram, which was a revered symbol of the Pythagorean Brotherhood” (Bellos, 2010, pg. 284). Shape, a core visual element within art, is vital to mathematics, as geometry is a part of it.
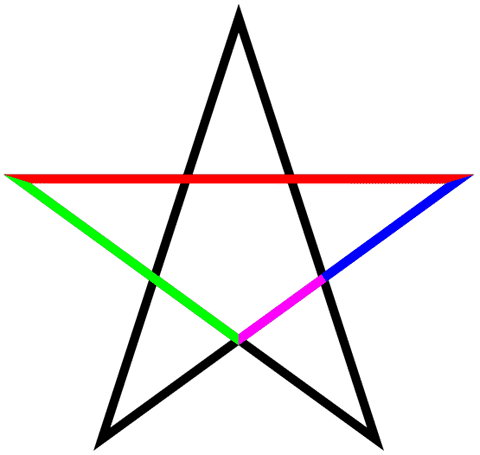
Phi within a pentagram
The golden ratio can even be extended to Fibonacci sequences (1,1, 2, 3, 5, 8…) as adding two previous terms to get the next equates to the golden ratio of 1.618033… as Bello (2010) states:
“adding two consecutive terms in a sequence to make the next one is so powerful that whatever two numbers you start with, the ratio of consecutive terms always converge to phi.” (pg. 291)

The Golden Ratio seen within the make up of a sunflower
This emphasises that phi is so crucial to the natural world and it’s symmetrical properties and that it not just a random number chosen by Euclid. So much so, that we, as a species, have utilised it when exploring painting, architecture and nature. These are all areas stemming back to creativity and art and can be seen being explored by great mathematicians and artists alike. A crucial part of Fibonacci sequence theory is that it is periodic, which means that every new term can only be created by the value of the previous terms. This stems well with a theory that links Fibonacci sequences and phi to nature because plant life forms expand through recurrence and can be followed through a being’s lineage (Atanassov, 2002).
Da Vinci used the golden ratio in many of his artworks and numerous historians argue that this is why we find them so aesthetically pleasing. It’s natural, based on the concept of phi.
What I found really important about this discovery was the connectedness of Mathematics through the history of art, and it’s prominent role on expression from the greats like da Vinci. This brought me back to Ma’s belief that the core aspects of mathematics coexist and are forever dependent on one another:
“A teacher with profound understanding of fundamental mathematics has a general intention to make connections among mathematical concepts and procedures…” (Ma, 2010, pg. 122).
In order for students to really grasp what they are learning, they need to see how their learning is important in a wider context. They need to be made aware of the journey that they are venturing on in their academia. Gone are the days of learning formulas for the sake of passing an exam.
I have found this blog post to be very therapeutic because I have had to learn so much in order to formulate the complexities of mathematics within art in my own words. I feel that this has benefitted my overall understanding of the link between mathematics and art. On practice, Fibonacci sequences could be interlinked with a topic on plants and could allow children to see the cross-curricular benefits mathematics has, not only in school but also in the real world. Not only that, a class could create their own symmetrical art using shapes that follow the golden ratio… The possibilities are endless!
Overall, art and mathematics have long been connected throughout time. It has only been through the dated teaching methods of rote learning and regurgitation of formulae that has hindered the broader prospects mathematics has on the wider world, in particular with creativity and artistic freedom.
Reference:
Atanassov, Krassimir T. (2002) New Visual Perspectives on Fibonacci Numbers New Jersey: River Edge
Bello, Alex (2010) Alex’s Adventures in Numberland London: Bloomsbury
Ma, Liping (2010) Knowing and Teaching elementary mathematics: teachers’ understanding of fundamental mathematics in China and the United States New York: Routledge.
McNiff, Shaun (2006) Art-based research 5th edn. Jessica Kingsley Publishers: London
