Category Archives: edushare

Conclusion to Discovering Mathematics

Wow, what a quick semester and elective, exciting learning opportunities and interesting facts and information about maths. Discovering mathematics has broadened my mind to the idea that maths is all around us and is very important in general day to day life of everyone not just, mathematicians, scientists, teachers, doctors etc.

Mathematics has been explored throughout the first semester of 2nd year and in many different ways. Art, music, Fibonacci, games and puzzles, statistics, science and gambling to name but a few. Each topic was explained in detail with extra reading to inform further about the subject. The lectures had a lot of practical and investigative/practical work which made it engaging and enjoyable. It is quite amazing how so many different areas require mathematical knowledge to be successful.

With the help of Ma (2010) and her explanation of Profound understanding of mathematics (PUFM), I have begun to broaden my knowledge and mind. The different factors which are crucial in PUFM are longitudinal coherence, connectedness, basic ideas and multiple perspectives. Presented with this list at the beginning of the module I was, to say the least, clueless but now having researched these they have become a lot clearer and not just words on a page. Each of the four is so important when learning and teaching mathematics and I think if I include this in my learning throughout my university time and into my teaching, I will be a stronger person in teaching mathematics and other curricular areas. I will understand why they are being taught and their importance to get the best from the children that I will be teaching.

Overall, this has been a worthwhile module in my general development as a student teacher as it has captured ideas about mathematics which are crucial but also broadened my mind in general about the importance of variation of teaching. The importance of teaching subjects together and not as an individual with the likes of maths and science combined. Making the subject enjoyable and accessible for all will hopefully increase the competency in mathematics and in turn eventually help to close the attainment gap which the Scottish Government is trying to do. They are trying to do this by increasing numeracy and literacy rates in children which in turn should make a smaller gap in what is achieved in different areas of the country who may have different opportunities.

Ma, Liping. (2010) Knowing and Teaching Elementary Mathematics: Teachers’ Understanding of Fundamental Mathematics in China and the United States. New York: Routledge.

Scottish Government. (2015) Closing the Attainment Gap. Available at: http://www.gov.scot/Publications/2016/06/3853/2 (Accessed: 5 March 2017)

Maths, statistics, studying medicine in Dundee……..

Leave a reply

After a fantastic lecture from Dr. Ellie Horthersall about maths, statistics and medicine in Dundee I felt inspired to write a blog post and look further into the statistics of the public health sector. Ellie trained as a doctor and now lectures at the University of Dundee as well as working in the pulic health sector dealing with statistics on a daily basis. Firstly she informed us of the statistics used for students who get onto the course which are very complicated and it is very rigorous. Each student has to complete a UCAS form and a UKCAT test which involves lots of problem solving and mathematics. Each of these tests are then merged together to calculate whether or not they can be accepted onto the course. Ellie explained how Dundee University is trying to change the norm of student doctors being middle class, white, very intelligent people and they are looking at getting students from different backgrounds onto the course whom show potential.

Statistics is all about maths but there is also a lot of common sense when understanding some of the maths within simple statistics. More complex statistics are very tricky to understand and takes experts in the field to decipher them. Ellie talked about many statistics which are used within the Public health sector. Statistics are gathered for example, for the average growth of a baby while in the mother’s womb so it can be compared to see if the baby is developing correctly or not. These statistics will help Doctors and Midwives check whether the baby is growing at the correct speed depending on the time of measurement and if there is a problem they will be able to do more tests which may determine why there is a change in development. This data is very useful and helps to identify different problems which the mother carrying the child may have which in turn will prompt the doctor to have more regular scans or checkups.

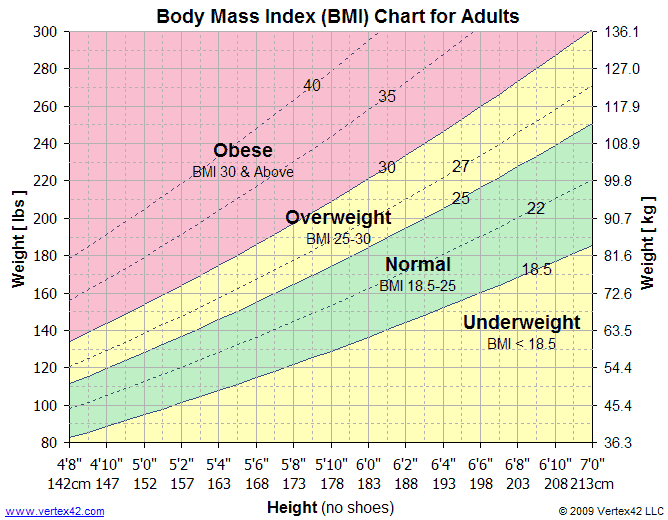
BMI is another statistical chart which is used by doctors to determine whether your height matches your weight in being of a healthy weight to being underweight or obese. This is a very general chart which may be invalid if you are a bodybuilder or long distance runner. Example of a BMI chart below:

Maths is crucially important for nurses, as well as doctors as a huge amount of their job, requires the use of maths and for example a SEWS (Scottish Early Warning Score) or NEWS (National Early Warning Score) Chart which is filled in when a patient is in a hospital several times throughout the day. These have several areas which I have researched through the Royal College of Physicians and these include; respiratory rate, oxygen saturation, temperature, systolic blood pressure, pulse rate, level of consciousness. Each of the 6 are scored each time the patient is checked depending on how unwell they are and a score is calculated. This will alarm the nurse if it is high or low which they will check again in case there was a mistake or phone the doctor for assistance. This is a very handy tool for doctors and nurses to use in a hospital ward for each patient. An example of a SEWS chart can be found here: http://journals.plos.org/plosone/article/figure/image?size=large&id=10.1371/journal.pone.0087073.g002

Other jobs which the medical profession require maths for are:

Drug doses (per kg for children)
Fluid prescribing
Biomechanics
Pharmacodynamics
Biochemistry
Interpreting research and probabilities

These are all really crucial parts of mathematics which if they get wrong it could cost the life of a patient which has happened before with over-prescription of drugs such as morphine. In the article below doctor gave patient six times the amount of a painkiller than he was supposed to. This resulted in the doctor having a 15month suspended jail sentence for her manslaughter. http://www.yorkshirepost.co.uk/news/doctor-bitterly-regrets-morphine-overdose-1-2300386

There are a huge amount of other statistics which are gathered by the government and public health to create life expectancy tables, an effect of vaccines, hospital mortality ratios, patterns in diseases to name but a few. These tables which are created show a general idea of each area but don’t actually look at the reasons why. There are many reasons why the life expectancy may be lower in one part of Scotland to the likes of London for example. Deprivation, money, poverty, access to good health care…. the list goes on. Each of these factors influences the life expectancy of an area. Other things such as boy racers getting killed in one year in freak accidents may also influence that year’s life expectancy figures. To calculate the life expectancy in a year all that is done is the ages of the people that have died in that year is added up and divided by the number of people that died. The table below also shows the difference in life expectancy between women and men which is between 5 and 10 years of difference.

An article on the BBC news looks at the life expectancy difference between women and men reducing: http://news.bbc.co.uk/1/hi/health/7699457.stm

Australian Government explains how life expectancy can be impacted:

“Life expectancy is affected by many factors such as: socioeconomic status, including employment, income, education and economic well-being; the quality of the health system and the ability of people to access it; health behaviours such as tobacco and excessive alcohol consumption, poor nutrition and lack of exercise; social factors; genetic factors; and environmental factors including overcrowded housing, lack of clean drinking water and adequate sanitation.”

These factors are also apparent in the UK and Scotland and do affect the life expectancy in different parts.

At the end of her presentation, Dr. Ellie explained the importance of teaching mathematics to children of a young age and the profound understanding of fundamental mathematics (PUFM) is essential in all medical professions and starting in the Primary school is essential to build up their knowledge. I also feel that mathematics is essential for everyday life and as Ma (2010) suggests each of her PUFM concepts of connectedness, basic ideas, longitudinal coherence and multiple perspectives are all so crucial when developing in further in life and learning. Teaching mathematics requires the in-depth knowledge of not just how to do the problems but also why and teachers with a PUFM are able to explain maths better to children and make it more enjoyable and encourage the children to understand mathematics to a higher level.

Overall a fantastic insight into the life of doctors and health care professionals use of statistics to do many things within their jobs.

References:

Australian Government (2012) Life Expectancy and Well-being. Available at: http://www.health.gov.au/internet/publications/publishing.nsf/Content/oatsih-hpf-2012-toc~tier1~life-exp-wellb~119 (Accessed: 11 Nov 2017)

BBC News (2008) Life expectancy gender gap closes. Available at: http://news.bbc.co.uk/1/hi/health/7699457.stm (Accessed: 11 November 2017)

Hothersall, E. (2017) Numeracy: Every contact counts (or something) [Lecture to MA2 Education Students] Discovering Mathematics. University of Dundee: 9 November.

Ma, Liping (2010) Knowing and Teaching elementary mathematics: teachers’ understanding of fundamental mathematics in China and the United States. New York: Routledge.

The Royal College of Physicians. (2015) National Early Warning Signs (NEWS). Standardising the assessment of acute-illness severity in the NHS. Available at: https://www.rcplondon.ac.uk/projects/outputs/national-early-warning-score-news Accessed: 10 November 2017

Music – how many beats in a bar……..Maths

Leave a reply

Maths and music – how do theserelate? – the first question I asked when going to the lecture. This threw me, but I was very interested to learn why maths and music related to each other. I do not play a musical instrument myself but I enjoy listening to music. A fantastic quote highlighted by Paola in the lecture is by Macus du Sautoy showing the importance of music and maths:

“Rhythm depends on arithmetic, harmony draws from basic numerical relationships, and the development of musical themes reflects the world of symmetry and geometry. As Stravinsky once said: “The musician should find in mathematics a study as useful to him as the learning of another language is to a poet. Mathematics swims seductively just below the surface.”

Marcus du Sautoy (2011) – this quote directly highlights the importance of mathematics for musicians as without mathematics there wouldnt be music.

When asked to think about it more deeply it was clear that maths and music were closely related and in my pair we came up with 3 or 4 different reasons. We came up with rhythms, beats in a bar and scales just from thinging more deeply about music and mathematics. There are also several more which I will list below:

Note values
chords
counting songs
fingering on music
time signature
figured bass
scales
mucial intervals
fibonacci sequence …… (shocked to see this again after it being so important in maths and nature!)

This lecture was very hands on with the use of musical instruments such as the glockenspheil, tamborines, rhythm sticks etc. Each of us were set into pairs and rows and firstly had to follow a very simple… rhythm. Simple for the people with rhythm I suppose. Each of the rows then had a different rhythm each and had to play it at the same time… very complicated for me and I found it quite a challenge but it showed that for different beats played together we created the backing to a song.

Music and the Fibonacci sequence

Fibonacci sequence – 1, 1, 2, 3, 5, 8, 13, 21……

How does this relate to maths, well…

There are 13 notes in an octave
A scale is composed of 8 notes
The 5th and 3rd notes of the scale form the basic ‘root’ chord and
are based on whole tone which is 2 steps from the root tone, that is the 1st note of the scale.

Each of the numbers mentioned are in the Fibonacci sequence – coincidence or not?

Continued:

The piano keyboard scale of C to C has 13 keys of which:
8 keys are white
5 keys are black
These are split into groups of 3 and 2

Wow… I am truely interested in how this is the case, is it just because thats how it has always been or was music influenced by the golden ratio and Fibonacci.

Pentatonic Scale

I guessed that it was something to do with five which is correct and I will explain further what it is. Bobby McFerrin does this very well.

The Pentatonic scale comes from the greek words pente – five and tonic – tone. It consists of 5 notes within an octave. Lots of songs are made up of pentatonic scales and Howard Goodall shows this in 5 different songs from all over the world:

Its amazing how much maths does relate to music in so many different ways which I have found very interesting to look at. As I am not a musician I thought I would find the concept difficult to understand but with excellent tuition from Paola it has become a lot more clear. My mind has been opened up to the reality that maths has a strong relationship with music and there are also many more ideas which I have just touched on which could be expanded even more.

https://www.goldennumber.net/music/ – explanation of Fibonacci and music.

Du Sautoy, M. (2011). ‘Listen by numbers: music and maths’ Guardian. Available http://theclassicalsuite.com/2011/06/listen-by-numbers-music-and-maths-via-guardian/ (Accessed: 04 November 2013)

Estrella, E. (2017) What are Pentatonic Scales. Available here: https://www.thoughtco.com/the-pentatonic-scales-2456569 (Accessed: 11 November 2017)

http://www.bbc.co.uk/programmes/p003c1b9

Sangster, P (2017) Discovering Mathematics; Music and Maths. [Lecture to MA2 Education Students] ED21006: Discovering Mathematics. Dundee University: 2 November 2017

Maths and Art

Leave a reply

There are many aspects of art which relate to maths and this was explained in an input from Anna Robb. The part which captured my interest straight away was how Fibonacci affects so many different things in nature and other places.

I taught the Fibonacci sequence at my school placement in first year when we were doing sequences within the maths topic. The sequence is – 0, 1, 1, 2, 3, 5, 8, 13, 21, 34……… The Fibonacci sequence is created from adding the previous number to the next so 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5……. Some children were able to work this out straight away and others struggled. I think the more advanced children who were able to work this out would be interested in the different parts of the Fibonacci sequence which relate to other parts of the world other than just a sequence. Actually using the facts of Fibonacci would make it more relevant to their learning and would capture their interest and promote their maths knowledge and understanding.

Bellos looks into the Fibonacci in nature even more with the garden as he looks at the number of petals on flowers – 3 petals: lily and Iris, 5 petals: pink and buttercup, 8 petals: delphinium…. Each of these numbers is in the Fibonacci sequence and furthermore, the likes of sunflowers, pinecones, and others relate to this too.

The golden rectangle and logarithmic spiral are both related to Fibonacci and we created the spiral in our maths and art input. To create this spiral using the sequence each square is placed beside each other. This is mind-blowing when it is compared to nature and a nautilus shell which has the exact same spiral as the one created by the Fibonacci sequence.

Each of these examples emphasises the connectedness of history of maths and art. Connectedness is one of the fundamental principles which Liping Ma highlights in her revolutionary book about teaching mathematics and the importance of profound understanding in fundamental mathematics.

Reference:

Bello, Alex (2010) Alex’s Adventures in Numberland London: Bloomsbury

Ma, Liping (2010) Knowing and Teaching elementary mathematics: teachers’ understanding of fundamental mathematics in China and the United States New York: Routledge.

Robb, A. (2017) Maths and Art [Lecture to MA2 Education Students] ED21006: Discovering Mathematics. Dundee University: 26 October 2017.

Probability in Mathematics – to gamble or not to gamble…

1 Reply

Personal opinion

Having never been a gambler myself I felt this was an interesting topic to cover in the Maths elective as I have always thought that the bandit/casino/dealer always wins. I have always said that I would only gamble if I had money to throw away and up to this time in my life I have not had excess cash to waste gambling.

My theory (having watched people gamble and from my dads advice) that the casino/bandit/slot machine wins is backed up by Bellos (2011) in Chance is a Fine Thing chapter where it starts with the explanation of machines in the US making ‘$25 million dollars’ after they have paid out the winnings. This shows that maybe one person might drop the jackpot in every few hundred people that play it but the gamblers don’t actually win in the long run.

Lottery

Gambling takes many forms but the probability of winning depends on what you play. Likes of the lottery the probability of winning the Jackpot is approximately 1 in 14million but this does not discourage people from playing it as there is a very small chance. Stefan Mandel proved that he could win the lottery in Virginia with every possible combination bought from stores which was a very laborious task and took a huge team of people to do this. The video below shows how his system worked.

Probability of a dice

Dice have 6 sides and if rolled could land on 1, 2, 3, 4, 5 or 6 – there is a 1 in 6 chance it will land on one of these numbers. But to roll two 6s with two dice changes the odds to 1 in 36 as there are many other options which could be rolled. The table below shows all the possible combinations that can be thrown with two dice which equals 36.

1	1	2	1	3	1	4	1	5	1	6	1
1	2	2	2	3	2	4	2	5	2	6	2
1	3	2	3	3	3	4	3	5	3	6	3
1	4	2	4	3	4	4	4	5	4	6	4
1	5	2	5	3	5	4	5	5	5	6	5
1	6	2	6	3	6	4	6	5	6	6	6

Roulette

Roulette has several ways of gambling – numbers, odd, even and colours – the table is shown below. People can bet on which number they think will come up and there is a screen which shows what numbers have come up which may influence peoples decisions to bet on different numbers. In the input on this particular area there was a video showing how Derren Brown wanted to beat the roulette table and memoriesd like a computer how to win it. This is a very difficult thing to do and takes many years of training to complete.

As mentioned at the start of this, I am not a gambler but after reading Bellos (2010) Chapter 9 has opened my eyes to what probability is and how it can capture people into thinking they can win. The odds for gambling and slot machines are set to make it impossible for the casino to loose in the long run as they are mathematically calculated.

Bellos, A. (2010). Alex’s Adventures in Numberland (Chapter 9). London: Bloomsbury

http://lottery.merseyworld.com/Info/Chances.html

http://datagenetics.com/blog/july12015/table.jpg

Investigating Volume – Regular and Irregular shapes

Leave a reply

Volume Definition – The amount of space that a substance or object occupies, or that is enclosed within a container.https://en.oxforddictionaries.com/definition/volume

Having enjoyed mathematics at school and knowing how to calculate volume it was interesting to find out today not just how to do it but also practical methods to show the children how to work it out. Calculating the volume of a cube is done by the formula length x breadth x height = volume (cm3) but there are many practical ways to do this with visuals to so how this works. We were asked to create a cube out of squared paper, scissors and sellotape. This was then used to fill with 1 cm cubes which shows how many fit into the cube looking at the volume. The picture below shows that I created a cube which was 5 x 5 x 5 which makes the volume 125cm3.

Allowing the children to make their own cubes with squared paper (a reasonable size – 3x3x3) and collecting enough cm cubes to put inside to count the volume will broaden their knowledge of what volume is and not just a formula. This is a great way to introduce volume as many find it a difficult concept but progressing on to using the formula is important as it would be near impossible to create a cube 100x100x100 and fill it with the cubes.

We then looked at the volume of a complex object such as plastic elephants which are used for counting, patterns etc in the early years. This is a whole different concept but children further up the school in P6/P7 may be able to grasp this. It involves water displacement and as shown in the photos when the elephants are added to the water the water rises in the beaker.

The beaker started with 100ml of water in it and when 6 small elephants were added it rose to 150ml of water showing that 6 elephants = 50ml so 1 elephant would = 8.333ml/cm3. This video shows measuring the volume of an irregular object. Using videos in class may also help to explain new concepts to children.

I felt that the importance of this lecture was to show that it is crucially important to us different methods for children to learn and make maths fun for all. Textbooks are useful for practice but learning different concepts most children will learn better hands on. This has been proven by many theorists who have done vast research in the field. Jo Boaler looks at this in her writing where she investigates instrumental and relational understanding in primary school through mathematics. My understanding of instrumental understanding is that it is learned by writing and following a procedure whereas relational understanding is learning what to do but also why you do it. This is key in maths and problem solving but actually in life as it is important that children learn what and why they are doing something and not just following a procedure.

Home

Boaler, J. (2009) The Elephant in the Classroom: Helping Children to Learn and Love Maths. London: Souvenir Press Ltd.

‘Stand and Deliver’ – Mathematics Films

Leave a reply

Inspired by the introduction of Discovering Mathematics I felt intrigued to watch the film which was suggested for TDT number 1. I enjoy watching films for leisure but also having a reason to watch this film and take some notes during it made me enjoy it even more. Stand and Deliver looks at the journey a very determined teacher who teaches a class with lower ability Calculus (an advanced level of mathematics using lots of different formulas).

At the beginning of the film, the class were disrespectful towards the new teacher as they tested his boundaries and methods. I found it very interesting how Jaime Escalante didn’t put up with any poor behaviour and gained the respect of his class very quickly.

The simple examples which he started with such as visuals bringing in apples and cutting them at the front of the class captured the attention of the students.

Notes which I observed from the film:

Explaining positive and negative numbers by using the beach and digging a hole – actually allowing the students to visualise how numbers work and not just the answer
Using repetition – e.g. negative x negative = a positive – the whole class repeated this after him many times, this could help store different methods in their memory. At the end of the repetition, he then asked the question WHY? This is showing that there is a reason for calculations.
Escalante was very encouraging and wouldn’t settle for second best – ensuring his pupils felt valued
Very determined teacher and not willing to give up but fight for his classes rights even though his health was suffering.
Built up a professional but also a personal relationship with his class and took interest in all his pupils.

The overall message which I got from this film was as a teacher it is crucial to build up a solid relationship with the class and show that you are working hard for and with them. It is also important to make math’s real life so the class can visualise what you are trying to teach which they may not get with examples in a text book.

This video shows the repetition of the class and teacher:

Design Technology – MA1

Leave a reply

The Design technology inputs have been very interesting this year in semester 2 of MA1. The first one involved simple manipulative skills such as using scissors and making a ladybird which could be done in many different age groups and classes. For each ladybird to be different the child can make their own templates which then ca 16930719_10209629972120930_1942021203_o n be cut out and attached with a split pin. These can be created to make show me boards if laminated, have different numbers or calculations which the children can challenge themselves or others with. Creating learning intentions for these topics are quite challenging as they have to relate to the skills being used and not the actual activity. 16936072_10209629972480939_1986658517_o

Learning Intention – We are learning to use scissors correctly

Success criteria – I can hold scissors correctly, I can hold the paper steady with my other hand, I can cut around the line drawn…

The next input involved using hammers, hand drills, G Clamp and Browder which can all be used in the classroom with lots of different stages and improve the children’s manipulative skills, fine motor skills and control. In groups, we had to teach others how to use these items and also discuss what they would be used for.

The follow up to this lesson was creating an item for a play park using a selected mechanism such as cams, pulleys, levers, pnumatics, hydraulics etc. For this design project, we were split into groups of three and had to create a new piece of equipment with hammers, nails, wood, and the above mechanisms. Allan, Liam and I created a climbing frame with a pulley system to take sand from the sandpit and take it to the top of the climbing frame to make sandcastles there. We were happy with our creation and felt that it could be used with a middle or upper class in school over several lessons.
16936354_10209629970080879_101524933_o 16880843_10209629969200857_551766057_o

Reflection on Semester 1

Leave a reply

An eye opener which struck me and I feel that I can reflect on in semester 1 is the working together module and visit to Dundee Children and Families Social Work Department in Lochee. This was a very impacting visit and I feel even though I am not naive to the world I didn’t realise to the extent of child neglect in and around Dundee. With a fantastic group of 10, we all worked together to come up with questions for the department visit. The manager, family support worker and newly appointed social worker all talked to us about their role in the area and also about why it was so important to work together with schools, social work and CLD to create a collegiate society all with the child in the centre.

Reflecting on this visit it was a fantastic opportunity to get a real insight into what happens day to day in a children and families social work department. As I am studying primary teaching it was interesting for me to see a different occupation and the importance of it in Dundee. The passion from our speakers was also very evident throughout the 2/3 hour visit and they were very descriptive and enlightening.

With the Working Together module being multidisciplinary I was able to work alongside trainee primary teachers, social workers and CLD students. We shared our opinions and listened well as a group with equal contribution and felt we clicked as a whole group. With the visit, we had to create a presentation as a group to highlight key areas for discussion and we worked hard together and managed to get a good result.

Overall a fantastic visit and experience working together to improve our understanding of the importance in future career to have the child at the centre. Also the importance of working alongside many different people to create a safe, healthy, achieving, nurturing, active, respected, responsible and included (SHANARRI) environment for the children in our care and in the community around. (word press representing good team working)

Drama TDT 1

Leave a reply

With very little knowledge or experience of drama before completing this TDT, I firstly had to research what conventions in drama were and also look at the experiences and outcomes in expressive arts to familiarise myself with them. Conventions otherwise known as techniques are the ways in which you work and move to create a desired dramatic effect or style. Woolland (2013)

Having researched this, I was then able to watch and evaluate the video given in the TDT.

The lesson which was being delivered to primary teachers in a CPD (Continual professional development) style showing them different ways in which to teach their classes. The structure was very clear with rules at the start showing the expectations of the tutor. This would be beneficial for the children as well highlighting to them key rules and behaviours in drama. They used the three C approach with communication, cooperation and concentration. All three were explained and there was a poster on the wall so they could be referred back too if there was any breakdown during the lesson. I thought this was an excellent idea as it builds up the expectations of the class from the teacher. This could be discussed before going to the area where drama is taking place and refreshed when in the space.

Following the rules there was then a warm up which allows the children to get ready for their drama session ahead which differentiates it from the previous lessons. Warm ups could include vocal, concentration, team working and also physical activities. After the warm up there was a stimulus of photographs of a village in India and this caused great discussion and is an effective way to start off the drama session of setting the scene. It also brings in a geography aspect which is a sign of interdisciplinary learning.

Soundscape – having the children imagine what the sounds would be like in the village with the beginning of a story (tapping on shoulders for response as the children will have their eyes shut)
Bodyscape – now moving on to making images from just their bodies from a story thought of by the teacher relating to the topic involved.
Still image – use of different levels with some standing and other lying, kneeling or sitting down portraying a image without movement directed by the teacher
Thought tracking – another way of gaging what is going on in the children’s mind by selecting a few children to share what they are thinking during a still image relating to the topic
Performing – this doesn’t have to happen every drama lesson but it is good to have the children being an audience but as well as showing their work during the lesson to the rest of the class. Some children will love to perform where as others will shy away but it is all about learning
Evaluating – must be done at the end of each drama session to make it meaningful and also so the teacher can see what the children have learned and their feelings about the class. The evaluation time will also allow for the children to calm down after an active and exciting session.

The benefits of the structure of this lesson is that it is very progressive starting with an image on a piece of paper and then having a still scene created by groups of children by the end. Voice is also used by creating the sounds of the village in this case but depending on the topic could be anything. I thought the conventions which were used in this clip were Structure and Story as they used still image and at the end were given a short script which they needed to act out.

CfE experiences and outcomes for Expressive Arts

I have chosen two which I feel relate to this lesson if delivered to children:

I use drama to explore real and imaginary situations, helping me to understand my world

(EXA 0-14a)

I can create, adapt and sustain different roles, experimenting with movement, expression and voice and using theatre arts technology (EXA 2-12a) Scottish Government (No date)Overall with a fantastic input 1 on drama and an interesting

Overall with a fantastic input 1 on drama and an interesting TDT I feel a lot more excited about teaching drama to my pupils in the future and also to further drama inputs.

Reference: Scottish Government (no date) Curriculum for Excellence: Expressive Arts Experiences and Outcomes. Available at: https://www.education.gov.scot/Documents/expressive-arts-eo.pdf [Accessed: 24th January 2017]

Wooland, B. (2013) Teaching Primary Drama. USA:Routledge.