I chose to take the elective of discovering mathematics mainly because of my fear of maths. Before choosing my elective, I had a look at all of the choices given to me. Originally, I was going to take French as my elective but as I am fluent in French already, I did not feel that this elective would be challenging enough for me.

When looking at the Discovering Mathematics elective, it explained that it was to increase the confidence and competence in maths. I felt that this would not only help me develop my knowledge in maths, but also help me overcome my fear of maths. For me, I need to work on my confidence level in maths and I feel that this would provide me with the opportunity to do so.

My past experience of maths was not great. I always had to work extra hard to achieve at least a pass in the subject! Although I did achieve a good grade in Immediate 2 mathematics, I had great difficulty in doing so. I had to work harder than the rest of the class and most of the time I had no idea what was going on and felt scared to ask.

I want to achieve confidence in maths and understand how and why mathematics is used n everyday life.

This picture sums up my previous experience in maths.

“Rhythm depends on arithmetic, harmony draws from basic numerical relationships, and the development of musical themes reflects the world of symmetry and geometry.  As Stravinsky once said: “The musician should find in mathematics a study as useful to him as the learning of another language is to a poet.  Mathematics swims seductively just below the surface.” Marcus du Sautoy (2011)

Believe it or not maths and music are very closely linked with one another. Which at first I wasn’t sure that there was a connection but after a lecture about this, I could see that this connection was more apparent than I had thought.

Here are some connections:

• Note values/rhythms
• Beats in a bar
• Tuning/Pitch
• Chords
• Counting songs
• Fingering on music
• Time signature
• Figured bass
• Scales
• Musical Intervals
• Fibonacci sequence

In the lecture about maths and music, the group were divided into 4 smaller groups. We were all given a bar to look at and clap out the beat. Every group was given a different line which they had to clap a different beat. This worked well as we were all able to clap in sync with one another. The bars that were given all added up to 8 and it was important that we were able to do this in order for this to sound good. This links with Ma’s Basic ideas as counting to 8 is very basic.

This activity would work well in a classroom setting as it may help children with their counting but also with their rhythm in music.

The Fibonacci Sequence and Music

“It is well known that the Fibonacci sequence of numbers and the associated “golden ratio” are manifested in nature and in certain works of art. It is less well known that these numbers also underlie certain musical intervals and compositions.” Gend (quoted in Vesic, 2014, p.72)

• There are 13 notes in an octave
• A scale is composed of 8 notes
• The 5^th and 3^rd notes of the scale form the basic ‘root’ chord and
• are based on whole tone which is 2 steps from the root tone, that is the 1^st note of the scale.
• The piano keyboard scale of C to C has 13 keys of which:
• 8 keys are white
• 5 keys are black
• These are split into groups of 3 and

All of these numbers appear in Fibonacci’s sequence. The Fibonacci sequence is seen everywhere around us and now, it is evident that it can also be heard in music. When it is seen in everyday life, it can be appealing to the eye but also now we can hear that it is appealing in the way that it sounds.

The picture here shows a piano piece which is based on the Fibonacci sequence.  The structure of the piece is based on groupings of bars into Fibonacci numbers, which gives the sense of growth of the whole work. The use of only Fibonacci notes works well for harmonious writing. It seems that the Fibonacci sequence works well in music and can sound very appealing to us without even knowing that the numbers are occurring.

Here is an example of the Fibonacci sequence in music. It is very relaxing and even I would listen to this while studying (mainly to keep me calm and distract me from becoming stressed.)

Patterns in Maths and Music

Maths and music are usually seen as two different subjects with no connections, However, it is important that children that children learn that there is a link which can be extremely important.

“Musical pieces are read much like you would read math symbols.  The symbols represent some bit of information about the piece.  Musical pieces are divided into sections called measures or bars.” Music, math, and patterns (no date)

The link between maths and music is patterns! We often look for patterns in maths which links to Ma’s idea of Basic ideas. Patterns in maths is often what children will initially look for which can be seen as a basic idea. This is similar in music as children will hear a pattern in music in repeating choruses and bars. In music, patterns can be recognised in notes. There may be a repeating high or low note throughout a piece of music.

Therefore, I believe that music and maths have a close relationship and children should be made aware of this.

• Gerben Schwab (2012) Fibonacci sequence in music. Available at: https://www.youtube.com/watch?v=2pbEarwdusc (Accessed: 21 November 2016).
• Maths in music: The secret mathematicians (2014) Available at: https://podcasts.ox.ac.uk/maths-music-secret-mathematicians (Accessed: 21 November 2016).
• Music, math, and patterns (no date) Available at: http://mathcentral.uregina.ca/beyond/articles/Music/music1.html (Accessed: 21 November 2016).

Before Mechanical Clocks

Before mechanical clocks were invented there were sundials, obelisks and water clocks which helped people tell the time of day it was. Sundials, obviously, told the time by the sun and the way it worked was with the shadows produced on the sundial. Sundials are the oldest known instruments for telling time. The surface of a sundial has markings for each hour of daylight. As the Sun moves across the sky, another part of the sundial casts a shadow on these markings. The position of the shadow shows what time it is. Water clocks, however, were used differently. Egyptian, Babylonian and others used ‘outflow’ clocks. Although in my opinion, water clocks would not be able to tell the exact time but would be able to show how much time had passed. They would also have to be refilled constantly in order for these to work.

Why 12/24 hours?

Egyptians had a theory and divided the time into 12 and 24 hours to determine the days.

10 hours of day

10 hours night

2 hours of half-light day (dawn)

2 hours of half-light night (dusk)

And these were arranged into 10 day groups (Decans – based on groups of stars)

This could possibly be the reason as to why we use 12 and 24 hour clocks.

Can animals tell time?

When this question was asked, I initially thought that it was possible but I couldn’t justify my reasons for this so I had to do some research into this. What I found was animals, such a birds, are able to understand the time of year as they fly south for the winter. Birds are aware of what time of year it is as they do this every year around the same time. This could just be because they start to feel the cold and are aware that this means the must fly south.

In my experience of animals and time, I have recently become more aware that maybe animals can tell time. I have a cat and he goes outside every night, around 10 o’clock and he is aware of this. Roughly at 10 o’clock, he will be waiting at the door ready to go outside for the night which indicates that he must have some sense of time. In the morning, when I get up around 7am, he is waiting at the door to come inside for the day. What I take from this is that he must be influenced by the sunlight but it could also be the length of time in which he is outside for.

Why do we need time?

Time is something I never seem to have enough of and I always say that there aren’t enough hours in my day to get anything done. Time is used every day by everyone. We need to know what time I must get up, what time I should leave to go to university in Dundee and how long it takes me to travel to university every day. If I don’t calculate this right, I wouldn’t make it for 9am lectures on time!

So I must calculate it like this if I have a 9am lecture:

• Wake up at 6.40am
• Leave the house at 7.45am
• Travel to Dundee (45mins – taking traffic into account)
• Arrive in Dundee at 8.30am (this ensure I have enough time to park my car and walk to the university)

I must work this out every day and this changes depending on what time my lectures start. So, I must use maths and time every day to ensure that I make it on time!

Is time linear?

In a recent workshop, the question was asked if we thought that time was linear. To me, this was a silly question because I had thought, of course time is linear that’s obvious! When looking into this it’s possible that we can actually time travel. This seems impossible but if we look at this with a different perspective, time travel is very possible.

Here is an example of time travel:

I travel to Switzerland at least 3 times a year. There is a time difference there of 1 hour. If I leave Scotland at 9am and it take 2 hours to travel there, I would arrive in Switzerland at 12pm. In Scotland it means that the time would only be 11am which means I have travelled forward in time!

Another example of this is:

If you were travelling direct from Australia to the UK it would take roughly 25 hours if travelling by aeroplane. This in effective is a whole day of travelling. If it is 10am in NZ on Wednesday 16^th of November, in the UK it would be 9pm on Tuesday 15^th of November. So, if you leave NZ at 10am on the 16^th of November, you will arrive in the UK on Tuesday 15^th of November. Therefore, you have traveled back in time!

Liping Ma (2010) suggests that to have a profound understanding of fundamental mathematics (PUFM) that you must have these 4 main principles which are, basic ideas, connectedness, multiple perspectives and longitudinal coherence. In this post, I will discuss my understanding of these 4 principles.

Basic Ideas
Liping Ma (2010, p.122) states that:
“Basic Ideas. Teachers with PUFM display mathematical attitudes are particularly aware of the “simple but powerful concepts and principles of mathematics” (e.g. the idea of an equation). They tend to revisit and reinforce these basic ideas. By focusing on these basic ideas, students are not merely encouraged to approach problems, but are guided to conduct real mathematical activity.”

Children should be taught basic ideas in maths in order to progress this idea into a more complex understanding of mathematics. Basic ideas should be easy to grasp before making the next step to further their understanding of a mathematical idea. If children are able to understand the basic idea in maths, it is important that this is reinfored before moving on to something more complicated.
If we start with the basic idea of addition and subtraction. It is important that before moving on to a topic such as money, they must have grasped how to add and subtract or they will be unable to understand how to use money correctly.

Connectedness
Connectedness in mathematics is a concept within maths that is connected to several other ideas.
“Connectedness. A teacher with PUFM has a general intention to make connections among mathematical concepts and procedures, from simple and superficial connections between individual pieces of knowledge to complicated and underlying connections among different mathematical operations and subdomains. When reflected in teaching, this intention will prevent students’ learning from the being fragmented. Instead of learning isolated topics, students will learn a unified body of knowledge.” (Liping Ma 2010, p.122)

This means that for a teacher to achieve connectedness they should not just teach maths as a single topic but link it to other topics which is an important factor as children need to be made aware as to why they are learning the mathematics in the first place. Children should be taught to make connections between mathematics and the real world and how maths is connected in everyday life, even if they don’t initially see it. For example, children can connect maths to things that they do in their everyday lives such as, baking and even going to the shops.
When teaching maths to children, it would be useful to incorporate this into different lessons. Instead of just teaching a maths lesson, a teacher could do a baking lesson and incorporating maths to highlight that these are connected. When teaching about money, children will be able to relate to this if they have been shopping with their parents. Looking at price labels, calculating the percentage discounts of reduced items and handling money and calculating change at the checkout can all contribute to children’s mathematical learning.
This connection to everyday life is important for children to understand as this will make their learning in class more meaningful to them.

Multiple Perspectives

Liping Ma (2010, p.122) states that to have a profound understanding of fundamental mathematics you must have multiple perspectives.

“Multiple Perspectives. Those who have achieved PUFM appreciate different facets of an idea and various approaches to a solution as well as their advantages and disadvantages. In addition, they are able to provide mathematical explanations of these various facets and approaches. In this way, teachers can lead their students to a flexible understanding of the discipline.”

This means that, when teaching maths in school, a teacher should have several different ways of coming up with a solution rather than one specific way. Sometimes when looking at something in a different perspective you are able to find the answer if you are struggling to do so. By providing multiple perspectives in class, it makes mathematics feel less restrictive to children. It is important that children should be taught to have multiple perspectives within mathematics as they will be able to see that there may be other ways to solve a problem, which may make solving a problem easier for them.

Longitudinal Coherence
Ma (2010, p.122) finally states that to have a profound understanding of mathematics, one must have longitudinal coherence.
“Longitudinal Coherence. Teachers with PUFM are not limited to the knowledge that should be taught in a certain grade, rather they have achieved a fundamental understanding of the whole elementary mathematics curriculum. With PUFM, teachers are ready at any time to exploit an opportunity to review crucial concepts that students have studied previously. They also know what students are going to learn later, and take opportunities to lay the proper foundation for it.”
This principle is one that I had great difficulty understanding at first. This suggests that when learning maths, the learner does not have a limit of how much knowledge that they have. I read into longitudinal coherence more and came across some reading that helped explain this so that even I could understand. Wu (2002) made this a lot easier for me to comprehend. Wu suggests that, as teachers, we make children of “individual trees clearly but, in the process, we short-change them by not calling their attention to the forest.” Which suggests to me that when teaching mathematics, we may only point out the most basic ideas but not the whole complex idea itself.

Wu (2002) also states that:
“We produce many students who do not think globally — or to use a more common word these days, holistically — about mathematics. In the present context, teachers who come through such a program may know the individual pieces of the school curriculum, but they are less adept at seeing the interrelationships among topics of different grades.”

I feel that Wu (2002) provided me with a far less complicated idea when it comes to longitudinal coherence. When teaching, it is important that encourage children to understand mathematics when teaching new topics. Pupils must be able to draw on their previous knowledge in mathematics to help them to understand new concepts. I feel that this is important to continue this throughout the children’s school life. Children should be able to draw on their previous learning in order to help them with their future development.

Although this concept still confuses me, I feel that I have developed a better understanding on what longitudinal coherence is.

Liping (2010) Knowing and teaching elementary mathematics: Teachers’ understanding of fundamental mathematics in china and the United States. 2nd edn. New York: Taylor & Francis.

Wu, H. (2002) What is so difficult about the preparation of mathematics teachers? Available at: https://math.berkeley.edu/~wu/pspd3d.pdf (Accessed: 31 October 2016).

If you had told me that maths was in art, I would have probably liked maths a lot more when I was a child. Maths can be seen everywhere in the world but I would never have thought that it was in art as well! To be honest, I would never have thought of the two subjects having any sort of connection.

If we take into consideration Liping Ma’s profound understanding of mathematics, it is mentioned that a teacher should have “connectedness.” This now makes sense to me as this I can now connect the two subjects together.

In a recent lecture, we spoke about Mondrian and created our own versions of these in class. At first, I did not see the relevance of this and thought to myself that this was just another piece of artwork that was displayed in the primary classroom.

The next part of the lecture was the interesting part. We were shown a sequence of numbers: 1, 1, 2, 3, 5, 8, 13…and asked what the next number and the rule was. I grasped this quickly as I have seen a sequence like this before. The next number is 21. Why? Because each term is formed by the sum of the 2 preceding terms. These numbers can go on and on to create much larger numbers.

The Golden Spiral

We were then given some instructions to draw a series of rectangles:

• Imagine the origin and put a dot in the center – this represents zero and is our starting point…
•  Draw a 1cm square from this starting point.
•  Draw a 1cm square adjacent to it, sitting on top.
•  Draw a 2cm square adjacent to the first two squares.
•  Draw a 3cm square adjacent to the three squares.
•  Continue with a 5cm square, am 8 cm square
• Use a compass. The pencil should sit at 0, the point should sit above. Draw a half circle through the two 1cm squares.
•  Move the point to 0 and continue the line through the 2cm square.
•  Move the point and continue the line through the 3cm square.

At first, I was completely baffled by this and had to start my example again. Once I had drawn the spiral within the rectangles I was left with a very aesthetically pleasing visual but still was not completely sure on the point of this example. We were told to pick out a rectangle within the visual and asked to divide the length by the width to see what number we ended up with. The number that we were all left with was the same, even though we did not all pick the same rectangle. This number was 1.6.

This is called the ratio of Phi or the golden ratio. In 1509, Italian mathematician Luca Pacioli published by Divina Proportione, a piece of work on a number that is now widely known as the “Golden Ratio.” This ratio, symbolised by Phi and it appears  in nature and mathematics (Pickover, 2009, p.112). Could Mondrian have used the Fibonacci sequence to create his most famous piece of artwork?

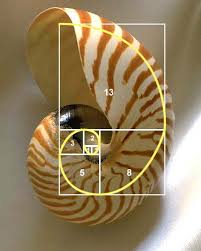
After further reading on this, I have discovered Fibonacci’s sequence and the Golden spiral can be seen in many different pieces of artwork. If we look at famous geometric shapes, many can be found in works of art such as the Fibonacci pine cone. This is a three-dimensional image, in which the petals of the pinecone are counted in a spiral downwards from the top of the cone. The Fibonacci numbers can be seen highlighted on this cone.

Fibonacci in Nature

One of the most interesting thing that I learnt about the Fibonacci sequence and the golden spiral is that it can be seen in nature. The fact that this sequence of numbers can be seen in in the world around us and in nature is fascinating! This spiral can be seen in shells, flowers, pine cones and even pineapples. I feel that this sequence must have a huge significance if it’s naturally occurring.

Fibonacci Sequence in Famous Art

As well as nature, the Fibonacci sequence can also be seen in works of art. This is because the sequence is considered a naturally graceful number sequence and using it is to create very aesthetically pleasing works of art or images, so many artists have used it to increase the visual appeal of their artwork. An example of this would be the Mona Lisa, which is one of the most famous paintings in the whole world. If you look at the image below, you can clearly see how the golden spiral fits in the painting. Mona Lisa’s face traces out the Fibonacci sequence.

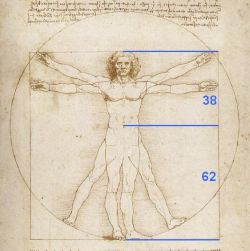
Another piece of artwork that this sequence can be seen in is Leonardo Da Vinci, The Vetruvian Man. However, this is seen in a different way from the previous piece of art. The ratio of the distance from the man’s feet to his stomach to the distance from the man’s stomach to his head is approximately the golden ratio of 1.6. Again this is shown in the image below.

Fibonacci in Famous Architecture

The ancient Greeks, Romans, Egyptians, and many others knew about the golden ratio. The Parthenon, which the Greeks constructed, has the golden ratio existing in many different places. The ratio of the width to the height of the building and the ratio of the height of the building to the height of the roof are both golden. Plus, the pillars in the front are placed so that the width of the building is split into a golden segment. The Egyptians used the golden ratio to build the famous Pyramids. The ratio of the side length of the pyramid to half the length of the base is the golden ratio.

Fibonacci around the house

Believe it or not you can see this sequence around your own house! As the golden ratio can be used in artwork to so that it is more visually pleasing, furniture designers use this sequence in their work to not only make it aesthetically pleasing, but also functional.

After having researched the Fibonacci sequence and the golden spiral, I am fascinated to see that it not only occurs in artwork to make it visually pleasing, but in the world around us!