I was a bit dubious before coming to this lecture and naively thought “what does maths have to do with art”. We had previously discussed the Golden ratio in previous lectures and I had not linked the two. My ideas, having only heard what the golden ratio was, was it made buildings look symmetrical – but again I thought that was perhaps to do with the structure etc.
We first looked at the Fibonacci sequence. Did he (Fibonacci) invent this sequence or merely discover its existence?
It goes, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 and so on.
The rule of this number series is the next term is formed by the sum of the two previous terms.
(There other rule is if you divide each by the number before it you will get 1.6 – sounds complicated and I will talk about this in another post).
This sequence seems simple enough however, we watched a video of how it explains rabbits and it was, to me, rather confusing. However, if you remove the part of where I watched the video I understand. The sequence is what it is and it makes sense to me. The rule is very simple to follow and it makes mathematical sense.
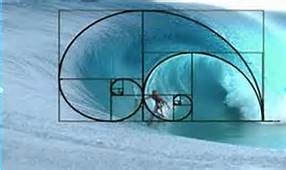
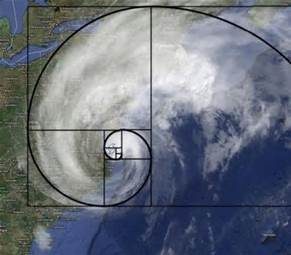
Golden Spiral
The Fibonacci number sequence is found in natural objects and phonema. For this to make sense
we drew the golden spiral based on the sequence above following written instructions of drawing squares but the number of squares followed the Fibonacci series. From the example you can from the squares drawn you can create a spiral.
This spiral is found in many natural objects and phenoma including:
So back to my earlier questions of did Fibonacci invent this sequence.
“We don’t invent mathematical structures – we discover them, and invent only the notation for describing them”. (Tegmark, 2014, p259).
It has been proven to us through many different examples such as the curve of a wave, nautilus shells, sunflowers, pineapples, the reproduction of bees and rabbits. The list goes on and on and now that I’ve seen it in so many different places and forms I will be on the look out. However, the sequence is recurrent according to Bello and the cyclical nature of it explains why it comes up in many natural life forms as they grow by a process of recurrence also (Bellos, 2010).
References
Bellos, A. (2014) Alex’s Adventures in Numberland. London. Bloomsbury.
Knott, R. (2010) Fibonacci Numbers and Nature. [Online]. Available at: http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibnat.html#petals (accessed 31/10/16)
Tegmark, M. (2014) Our Mathematical Universe.
