Monthly Archives: November 2017

Conclusion to Discovering Mathematics

Leave a reply

Wow, what a quick semester and elective, exciting learning opportunities and interesting facts and information about maths.  Discovering mathematics has broadened my mind to the idea that maths is all around us and is very important in general day to day life of everyone not just, mathematicians, scientists, teachers, doctors etc.

Mathematics has been explored throughout the first semester of 2nd year and in many different ways.  Art, music, Fibonacci, games and puzzles, statistics, science and gambling to name but a few.  Each topic was explained in detail with extra reading to inform further about the subject.  The lectures had a lot of practical and investigative/practical work which made it engaging and enjoyable.  It is quite amazing how so many different areas require mathematical knowledge to be successful.

With the help of Ma (2010) and her explanation of Profound understanding of mathematics (PUFM), I have begun to broaden my knowledge and mind.  The different factors which are crucial in PUFM are longitudinal coherence, connectedness, basic ideas and multiple perspectives. Presented with this list at the beginning of the module I was, to say the least, clueless but now having researched these they have become a lot clearer and not just words on a page.  Each of the four is so important when learning and teaching mathematics and I think if I include this in my learning throughout my university time and into my teaching, I will be a stronger person in teaching mathematics and other curricular areas.  I will understand why they are being taught and their importance to get the best from the children that I will be teaching.

Overall, this has been a worthwhile module in my general development as a student teacher as it has captured ideas about mathematics which are crucial but also broadened my mind in general about the importance of variation of teaching.  The importance of teaching subjects together and not as an individual with the likes of maths and science combined.  Making the subject enjoyable and accessible for all will hopefully increase the competency in mathematics and in turn eventually help to close the attainment gap which the Scottish Government is trying to do. They are trying to do this by increasing numeracy and literacy rates in children which in turn should make a smaller gap in what is achieved in different areas of the country who may have different opportunities.

 

Ma, Liping. (2010) Knowing and Teaching Elementary Mathematics: Teachers’ Understanding of Fundamental Mathematics in China and the United States. New York: Routledge.

Scottish Government. (2015) Closing the Attainment Gap. Available at: http://www.gov.scot/Publications/2016/06/3853/2 (Accessed: 5 March 2017)

 

Maths – Puzzles and Games

Leave a reply

For the last Discovering Mathematics input was with Richard and about something which has been a huge part of my childhood and I still enjoy now.  Puzzles and Games are a fond memory of my brothers and sisters playing different games in front of the fire as well as arguments and enjoyment.

The games which first come to mind are – Solitaire, Monopoly, Kerplunk, Frustration, Cluedo, Hungry Hippos, Trivial Pursuit, Draughts, Chess, Rapidough, Pictionary, Bingo, Uno, Snap, Snakes and Ladders, Charades all of which I have played as a child and older too. I was lucky as a child to have 2 sisters and a brother and we were very close in age, just a year apart! This allowed for us to play these games without parent supervision at times when we were not fighting about the rules.

Games the first time at university (when I was 18 and slightly less mature!) changed slightly and involved drinking too. These were – Shot Roulette, Ring of fire (car game relating to the number or suit on the card), Battleshots….to name but a few.  Even though these were usually played before going out also contained the use of mathematics too.  The mathematical parts to it would have been forgotten when there were a few too many drinks involved!  Interesting to think back now that there was maths involved with getting drunk over 7 years ago.

Games which were discussed at the lecture were – suduko and mennies which require lots of different skills such as problem-solving, positional understanding, counting and many more. Suduko doesn’t actually require arithmetic but requires maths such as problem-solving. Below is an example of how to solve a basic suduko.

 

Rubiks cube is another game which doesn’t require arithmetic but requires systematical thinking and can be learned.  The fastest person can do this in less than 5 seconds.  I really struggle with this concept as its very difficult to do but with lots of practice I am sure it could be completed.

Maths is amazing and if you look far into all the games there will be some sort of mathematical theory to it!  I find this fascinating and think that children would benefit from playing more games which challenge their thinking and problem solving and it will also make some of the lessons more fun.

I feel the importance of having puzzles and games for children during childhood is they build many different skills and most have fond memories of games.  With reference to Ma, 2010 who describes the Profound Understanding of Fundamental Mathematics with Basic Ideas, Longitudinal Coherence, Multiple Perspectives and Connectedness.  Using the basic ideas in games helps with the understanding and likes of the banker in Monopoly will have to do simple addition and subtraction which is part of this Basic Ideas concept.

Reference:Ma, Liping (2010) Knowing and Teaching Elementary Mathematics: Teachers’ Understanding of Fundamental Mathematics in China and the United States. New York: Routledge.

Ma, Liping (2010) Knowing and Teaching Elementary Mathematics: Teachers’ Understanding of Fundamental Mathematics in China and the United States. New York: Routledge.

Maths and Science

Leave a reply

Having done quite a lot of science throughout school and placement, I was aware that maths and science were closely related.  With this input, there were, even more, ideas highlighted which show the relationship.

Our first task in groups of 4 was to think of as many different ways in which maths and science are related – this seems easy until you are put on the spot to think. Our group came up with these:

  1. Hypothesis, estimates, predictions,
  2. elements
  3. statistics
  4. graphs
  5. measuring (weight …)
  6. sampling
  7. tables and graphs
  8. analysing

After getting these everyone shared their ideas with the class and other ideas were highlighted.  An example of a very mathematics equation related to a scientifc equation is:

e=mc2

This stands for energy = mass x (speed of light) squared which was a finding from the great Einstein 1943.

Another key skill in science which is closely related to maths is graph drawing and also analysing.  This can be quite a difficult concept for primary children but also anyone who hasn’t drawn a graph in a while.

This youtube video shows the simple steps to drawing a simple graph plotting the y and x-axes and then a scale.

Within science, graphs will be used to show changes or data and make it easier to analyse. There are many different types of graphs such as; bar graph, pie chart, linear graphs…. all of which can be used for different data analysis.  As the society is visually driven it is effective to have graphs and charts to show results of different experiments and data collection.

How to make a line graph – copied from (Why do scientists use graphs?)

  1. Label the x axis (horizontal axis) with the independent variable.
  2. Label the y-axis (vertical axis) with the dependent variable.
  3. Determine the range of your data that must fit on each axis. The range will set the scale.
  4. Number each axis division (line). Each division should be equally spaced.
  5. Plot each data pair accurately as a point on the graph.
  6. Choose a title that describes the graph.

This is basic instructions to introduce graph drawing.

Other areas where maths and science relate are; magnetism, electricity, forces, gravity and many more.

There are both maths and science in the Curriculum for Excellence which is used in Scotland.  The principles and practices can be found on the Education Scotland website as well as the outcomes and experiences which are guidelines for teacher which the children need to complete in their time in school.  There are some of the outcomes and experiences which can be cross curricular between science and maths which is likely to capture the children interest if its not just maths from a textbook but hands on data collection and analysis.

It is very clear after this input that Science is closely related to maths and one would struggle without the other.

Ref

Click to access Organizing%20Data.pdf

Click to access sciences-eo.pdf

Click to access numeracy-maths-eo.pdf

A revelation …. longitudinal coherence

Leave a reply

While researching for my Discovering mathematics essay I have massively broadened my own understanding of Ma (2010) key elements of profound understanding of fundamental mathematics (Basic ideas, connectedness, multiple perspectives and longitudinal coherence).  In particular, in this blog post, I am going to speak about Longitudinal Coherence which I honestly had no idea what it meant before starting this module in discovering mathematics. In Liping Mas’ Knowing and Teaching elementary mathematics book she describes it as:

“Longitudinal Coherence – Teachers with PUFM are not limited to the knowledge that should be taught in a certain grade; rather, they have achieved a fundamental understanding of the whole elementary mathematics curriculum. With PUFM, teachers are ready at any time to exploit an opportunity to review crucial concepts that students have studied previously. They also know what students are going to learn later, and take opportunities to lay the proper foundations for it.” (pg 122)

This is a direct quote from her book which I have read a few times and do understand but thought I should research further to find further meaning to longitudinal coherence. An excellent quote from a paper written by Wu (2002) has opened my mind even further:

“We endeavor to make students see the individual trees but, in the process, we shortchange them by not calling their attention to the forest.” (pg.16)

This quote followed by the explanation of fractions which I have inserted below has opened my mind to the importance of a teacher not only knowing what they are teaching but also being able to refer to other topics which will relate to the current one.  With this knowledge, the reinforcement of the basic ideas which is another key element of PUFM will broaden the knowledge of not only the pupil but also the teacher or student teacher.

 

 

Having researched this I feel for my own development in my student teaching leading onto my teaching career I need to build this PUFM throughout my time at university so I have a sound knowledge of what I will be teaching throughout the primary school.  I have enjoyed researching this and with the help of excellent scholars in this field, it has broadened my understanding of the importance of mathematics and the profound understanding of fundamental mathematics in schools.

 

Reference:

Ma, Liping (2010) Knowing and Teaching Elementary Mathematics: Teachers’ Understanding of Fundamental Mathematics in China and the United States. New York: Routledge.

Wu, H. (2002) “Longitudinal coherence of the curriculum” in What is so difficult about the preparation of mathematics teachers?. University of California: Berkley. Available at: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.15.9760&rep=rep1&type=pdf  Accessed 9 November 2017

Maths, statistics, studying medicine in Dundee……..

Leave a reply

After a fantastic lecture from Dr. Ellie Horthersall about maths, statistics and medicine in Dundee I felt inspired to write a blog post and look further into the statistics of the public health sector.  Ellie trained as a doctor and now lectures at the University of Dundee as well as working in the pulic health sector dealing with statistics on a daily basis.   Firstly she informed us of the statistics used for students who get onto the course which are very complicated and it is very rigorous.  Each student has to complete a UCAS form and a UKCAT test which involves lots of problem solving and mathematics. Each of these tests are then merged together to calculate whether or not they can be accepted onto the course. Ellie explained how Dundee University is trying to change the norm of student doctors being middle class, white, very intelligent people and they are looking at getting students from different backgrounds onto the course whom show potential.

Statistics is all about maths but there is also a lot of common sense when understanding some of the maths within simple statistics.  More complex statistics are very tricky to understand and takes experts in the field to decipher them. Ellie talked about many statistics which are used within the Public health sector.  Statistics are gathered for example, for the average growth of a baby while in the mother’s womb so it can be compared to see if the baby is developing correctly or not. These statistics will help Doctors and Midwives check whether the baby is growing at the correct speed depending on the time of measurement and if there is a problem they will be able to do more tests which may determine why there is a change in development. This data is very useful and helps to identify different problems which the mother carrying the child may have which in turn will prompt the doctor to have more regular scans or checkups.

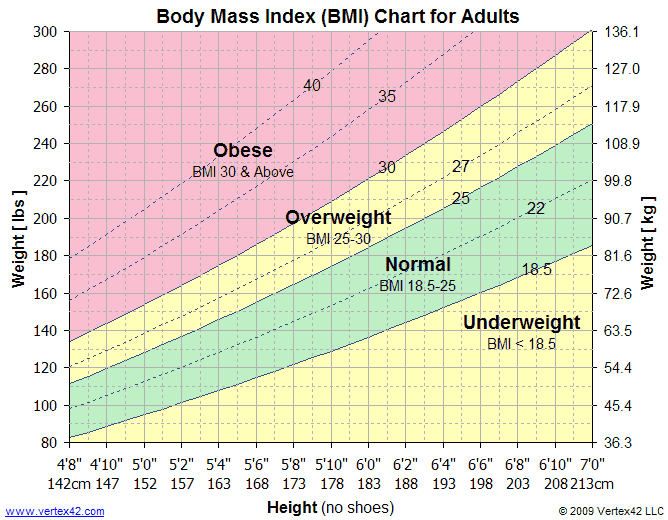
BMI is another statistical chart which is used by doctors to determine whether your height matches your weight in being of a healthy weight to being underweight or obese. This is a very general chart which may be invalid if you are a bodybuilder or long distance runner. Example of a BMI chart below:

Maths is crucially important for nurses, as well as doctors as a huge amount of their job, requires the use of maths and for example a  SEWS (Scottish Early Warning Score) or NEWS (National Early Warning Score) Chart which is filled in when a patient is in a hospital several times throughout the day. These have several areas which I have researched through the Royal College of Physicians and these include; respiratory rate, oxygen saturation, temperature, systolic blood pressure, pulse rate, level of consciousness.  Each of the 6 are scored each time the patient is checked depending on how unwell they are and a score is calculated. This will alarm the nurse if it is high or low which they will check again in case there was a mistake or phone the doctor for assistance.  This is a very handy tool for doctors and nurses to use in a hospital ward for each patient.  An example of a SEWS chart can be found here: http://journals.plos.org/plosone/article/figure/image?size=large&id=10.1371/journal.pone.0087073.g002

Other jobs which the medical profession require maths for are:

  • Drug doses (per kg for children)
  • Fluid prescribing
  • Biomechanics
  • Pharmacodynamics
  • Biochemistry
  • Interpreting research and probabilities

These are all really crucial parts of mathematics which if they get wrong it could cost the life of a patient which has happened before with over-prescription of drugs such as morphine. In the article below doctor gave patient six times the amount of a painkiller than he was supposed to. This resulted in the doctor having a 15month suspended jail sentence for her manslaughter. http://www.yorkshirepost.co.uk/news/doctor-bitterly-regrets-morphine-overdose-1-2300386

There are a huge amount of other statistics which are gathered by the government and public health to create life expectancy tables, an effect of vaccines, hospital mortality ratios, patterns in diseases to name but a few.  These tables which are created show a general idea of each area but don’t actually look at the reasons why.  There are many reasons why the life expectancy may be lower in one part of Scotland to the likes of London for example.  Deprivation, money, poverty, access to good health care…. the list goes on. Each of these factors influences the life expectancy of an area. Other things such as boy racers getting killed in one year in freak accidents may also influence that year’s life expectancy figures. To calculate the life expectancy in a year all that is done is the ages of the people that have died in that year is added up and divided by the number of people that died.  The table below also shows the difference in life expectancy between women and men which is between 5 and 10 years of difference.

An article on the BBC news looks at the life expectancy difference between women and men reducing: http://news.bbc.co.uk/1/hi/health/7699457.stm

Australian Government explains how life expectancy can be impacted:

“Life expectancy is affected by many factors such as: socioeconomic status, including employment, income, education and economic well-being; the quality of the health system and the ability of people to access it; health behaviours such as tobacco and excessive alcohol consumption, poor nutrition and lack of exercise; social factors; genetic factors; and environmental factors including overcrowded housing, lack of clean drinking water and adequate sanitation.”

These factors are also apparent in the UK and Scotland and do affect the life expectancy in different parts.

At the end of her presentation, Dr. Ellie explained the importance of teaching mathematics to children of a young age and the profound understanding of fundamental mathematics (PUFM) is essential in all medical professions and starting in the Primary school is essential to build up their knowledge.  I also feel that mathematics is essential for everyday life and as Ma (2010) suggests each of her PUFM concepts of connectedness, basic ideas, longitudinal coherence and multiple perspectives are all so crucial when developing in further in life and learning.  Teaching mathematics requires the in-depth knowledge of not just how to do the problems but also why and teachers with a PUFM are able to explain maths better to children and make it more enjoyable and encourage the children to understand mathematics to a higher level.

Overall a fantastic insight into the life of doctors and health care professionals use of statistics to do many things within their jobs.

References:

Australian Government (2012) Life Expectancy and Well-being. Available at: http://www.health.gov.au/internet/publications/publishing.nsf/Content/oatsih-hpf-2012-toc~tier1~life-exp-wellb~119 (Accessed: 11 Nov 2017)

BBC News (2008) Life expectancy gender gap closes. Available at: http://news.bbc.co.uk/1/hi/health/7699457.stm (Accessed: 11 November 2017)

Hothersall, E. (2017) Numeracy: Every contact counts (or something) [Lecture to MA2 Education Students] Discovering Mathematics. University of Dundee: 9 November.

Ma, Liping (2010) Knowing and Teaching elementary mathematics: teachers’ understanding of fundamental mathematics in China and the United States. New York: Routledge.

The Royal College of Physicians. (2015) National Early Warning Signs (NEWS). Standardising the assessment of acute-illness severity in the NHS. Available at: https://www.rcplondon.ac.uk/projects/outputs/national-early-warning-score-news Accessed: 10 November 2017

Music – how many beats in a bar……..Maths

Leave a reply

Maths and music – how do theserelate? – the first question I asked when going to the lecture. This threw me, but I was very interested to learn why maths and music related to each other.  I do not play a musical instrument myself but I enjoy listening to music. A fantastic quote highlighted by Paola in the lecture is by Macus du Sautoy showing the importance of music and maths:

“Rhythm depends on arithmetic, harmony draws from basic numerical relationships, and the development of musical themes reflects the world of symmetry and geometry. As Stravinsky once said: “The musician should find in mathematics a study as useful to him as the learning of another language is to a poet. Mathematics swims seductively just below the surface.”

Marcus du Sautoy (2011) – this quote directly highlights the importance of mathematics for musicians as without mathematics there wouldnt be music.

When asked to think about it more deeply it was clear that maths and music were closely related and in my pair we came up with 3 or 4 different reasons. We came up with rhythms, beats in a bar and scales just from thinging more deeply about music and mathematics.  There are also several more which I will list below:

  • Note values
  • chords
  • counting songs
  • fingering on music
  • time signature
  • figured bass
  • scales
  • mucial intervals
  • fibonacci sequence …… (shocked to see this again after it being so important in maths and nature!)

This lecture was very hands on with the use of musical instruments such as the glockenspheil, tamborines, rhythm sticks etc. Each of us were set into pairs and rows and firstly had to follow a very simple… rhythm.  Simple for the people with rhythm I suppose.  Each of the rows then had a different rhythm each and had to play it at the same time… very complicated for me and I found it quite a challenge but it showed that for different beats played together we created the backing to a song.

Music and the Fibonacci sequence 

Fibonacci sequence – 1, 1, 2, 3, 5, 8, 13, 21……

How does this relate to maths, well…

  • There are 13 notes in an octave
  • A scale is composed of 8 notes
  • The 5th and 3rd notes of the scale form the basic ‘root’ chord and
  • are based on whole tone which is 2 steps from the root tone, that is the 1st note of the scale.

Each of the numbers mentioned are in the Fibonacci sequence – coincidence or not?

Continued:

  • The piano keyboard scale of C to C has 13 keys of which:
  • 8 keys are white
  • 5 keys are black
  • These are split into groups of 3 and 2

Wow… I am truely interested in how this is the case, is it just because thats how it has always been or was music influenced by the golden ratio and Fibonacci.

Pentatonic Scale

I guessed that it was something to do with five which is correct and I will explain further what it is. Bobby McFerrin does this very well.

 

The Pentatonic scale comes from the greek words pente – five and tonic – tone.  It consists of 5 notes within an octave. Lots of songs are made up of pentatonic scales and Howard Goodall shows this in 5 different songs from all over the world:

Its amazing how much maths does relate to music in so many different ways which I have found very interesting to look at.  As I am not a musician I thought I would find the concept difficult to understand but with excellent tuition from Paola it has become a lot more clear.  My mind has been opened up to the reality that maths has a strong relationship with music and there are also many more ideas which I have just touched on which could be expanded even more.

https://www.goldennumber.net/music/ – explanation of Fibonacci and music.

Du Sautoy, M. (2011). ‘Listen by numbers: music and maths’ Guardian. Available http://theclassicalsuite.com/2011/06/listen-by-numbers-music-and-maths-via-guardian/ (Accessed: 04 November 2013)

Estrella, E. (2017) What are Pentatonic Scales. Available here: https://www.thoughtco.com/the-pentatonic-scales-2456569 (Accessed: 11 November 2017)

http://www.bbc.co.uk/programmes/p003c1b9

Sangster, P (2017) Discovering Mathematics; Music and Maths. [Lecture to MA2 Education Students] ED21006: Discovering Mathematics. Dundee University: 2 November 2017

Maths and Art

Leave a reply

There are many aspects of art which relate to maths and this was explained in an input from Anna Robb.  The part which captured my interest straight away was how Fibonacci affects so many different things in nature and other places.

I taught the Fibonacci sequence at my school placement in first year when we were doing sequences within the maths topic.  The sequence is – 0, 1, 1, 2, 3, 5, 8, 13, 21, 34……… The Fibonacci sequence is created from adding the previous number to the next so 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5…….  Some children were able to work this out straight away and others struggled.  I think the more advanced children who were able to work this out would be interested in the different parts of the Fibonacci sequence which relate to other parts of the world other than just a sequence.  Actually using the facts of Fibonacci would make it more relevant to their learning and would capture their interest and promote their maths knowledge and understanding.

Bellos looks into the Fibonacci in nature even more with the garden as he looks at the number of petals on flowers – 3 petals: lily and Iris, 5 petals: pink and buttercup, 8 petals: delphinium…. Each of these numbers is in the Fibonacci sequence and furthermore, the likes of sunflowers, pinecones, and others relate to this too.

The golden rectangle and logarithmic spiral are both related to Fibonacci and we created the spiral in our maths and art input.  To create this spiral using the sequence each square is placed beside each other. This is mind-blowing when it is compared to nature and a nautilus shell which has the exact same spiral as the one created by the Fibonacci sequence.

Each of these examples emphasises the connectedness of history of maths and art.  Connectedness is one of the fundamental principles which Liping Ma highlights in her revolutionary book about teaching mathematics and the importance of profound understanding in fundamental mathematics.

Reference:

Bello, Alex (2010) Alex’s Adventures in Numberland London: Bloomsbury

Ma, Liping (2010) Knowing and Teaching elementary mathematics: teachers’ understanding of fundamental mathematics in China and the United States New York: Routledge.

Robb, A. (2017) Maths and Art [Lecture to MA2 Education Students] ED21006: Discovering Mathematics. Dundee University: 26 October 2017.