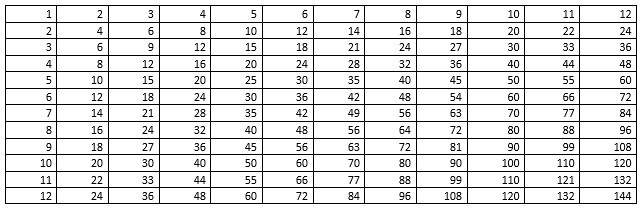
Below we can see the times table square going up to the number 12. After the lecture received today around the decimal place and number systems I became interested in how the 12 number system works. I wanted to investigate this further.

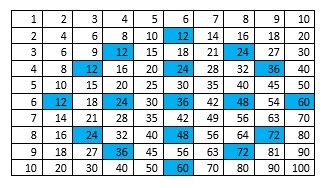
For starting I wanted to complete the times table grid first of all using the knowledge I already have. Then for changing the appropriate numbers into the corresponding symbols for the duodecimal system (changing 10, 11 and 12) I decided to highlight the certain numbers which relate to needing changed directly then adjusting the rest.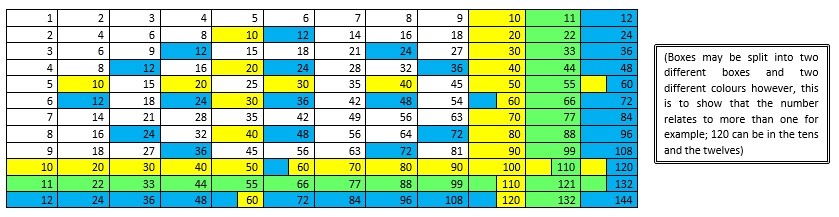

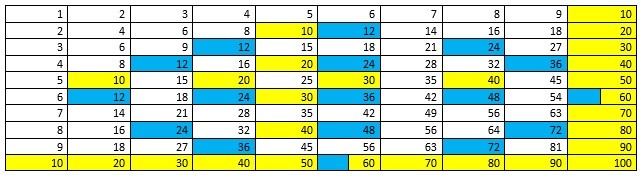
Through doing this I began to see a pattern emerging from the duodecimal system within the regular decimal system. First I realised that the 11 times table is obviously not included within the decimal system. However, the 12 and 10 systems are shown repeatedly within the decimal system (times table).

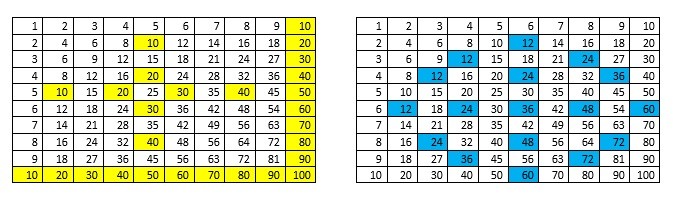
By colour coding the boxes differently (10 being yellow and 12 being blue) I could identify the different patterns, which were appearing, more clearly. As you can see below I then focused in on the individual systems on two separate tables.

 

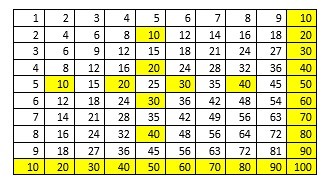
Looking at the 10’s diagram (on the left) we can see a pattern formed by the colours, taking away the numbers from the table we can see this more clearly.

 

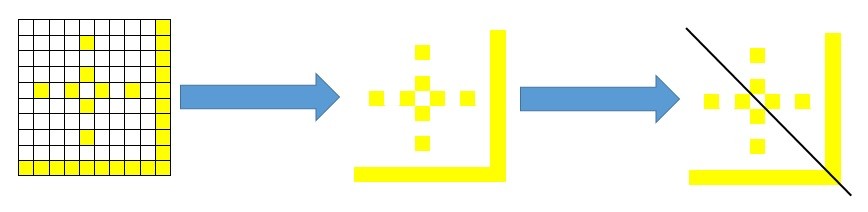
Immediately, I could see that there is the possibility of symmetry. By adjusting the cells to 0.5cm by 0.5cm squares you can see the one line of symmetry within the pattern (the line of symmetry is symbolised by the black line.)

 

The same occurs within the diagram of the 12’s system. Again if we take away the numbers and grid lines, looking at the pattern it is clear that there are more lines of symmetry than the 10’s system.

 

Resizing once again the table to squares of 0.5cm by 0.5cm. Here we have 4 lines of symmetry (identified by the black lines). However, unlike the last example this pattern has a rotational symmetry of 4.

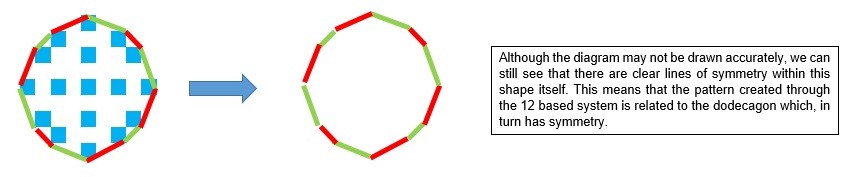
We usually relate symmetry to solid shapes and so, looking at a decagon and a dodecagon this can represent a 10 base system and a 12 base system. We can see that a decagon has 10 lines of symmetry and the dodecagon has 12 lines of symmetry. The decagon has 10 lines of symmetry and the dodecagon has 12 lines of symmetry.

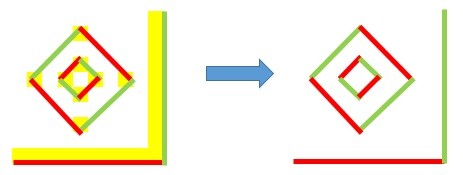
Comparing the patterns discovered from the base 10 and 12 systems we can see that there are some similarities. The base 12 pattern has, what could be, an irregular dodecagon outline. Looking at the diagram the red and green lines shows the connecting lines that form this shape.

This can also be explored within the pattern of the 10 based system. By connecting the diagram in a different way we can see that there are 10 different lines (shown in red and green) however, the lines are not connected entirely and so it cannot be expressed as a decagon.

It is possible that the reason behind these patterns, discovered from the 10 and 12 based systems, show elements of symmetry is because of the relationship with decagons and dodecagons. The 12 based system creates a pattern with clear lines of symmetry, which can be linked to the symmetrical shape that is the dodecagon. However, the shape created is not a regular dodecagon but an irregular dodecagon. Whereas the pattern from the 10 based system does not create a regular/irregular decagon. However, by connecting the points in a different way through using lines we can say that the pattern can be connected by 10 lines. This does have links to the decagon as it has 10 edges. Overall, I have explored the duodecimal system looking further into the 10 and 12 based systems to find the connection between the systems and symmetry as a result of using shape to understand this relationship.