Infinity. It’s about as big as it gets.
In our Discovering Mathematics input yesterday, upon discussing the vastness of the universe in which we live, the term infinity was mentioned. Simply put, infinity refers to something which never ends. A conceptual example of this would be natural numbers, of which, no matter how long you count for, there will always be more.
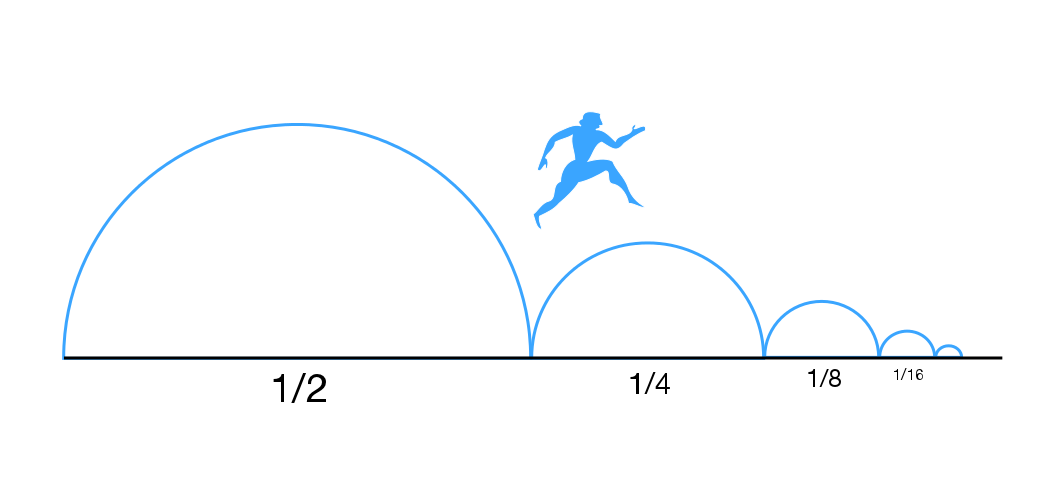
Greek mathematician Zeno of Erea is credited with being the first to investigate the infinity concept. Zeno’s exploration of infinity used an example of a journey to further understand the concept. He stated that to travel across a distance, first you must travel half the distance. So far not too difficult to understand. He then stated that from this halfway point you would then have to travel halfway again (this time half as far). Zeno claimed that even if this halfway process were completed an infinite amount of times, the destination could not be reached. Of course this exists as a paradox as we know that it is possibly to reach our destinations. A comparison could be drawn to the modern geometric progression that tends towards one (1/2 + 1/4 + 1/8 + …etc.) but never actually reaches the integer. Confusingly enough both of these processes involve an infinite number of steps to achieve a finite answer.
Much later in 1924, German mathematician David Hilbert designed a thought experiment to demonstrate the counter intuitive nature of infinite sets and further our understanding of the infinity concept. His example is know as the Hilbert Hotel paradox.
Consider for a moment a hotel which contains infinitely many rooms all of which were occupied by an infinite amount of guests. It would seem reasonable to assume that any newly arriving guests would have to be turned away. However this is where the idea of infinity becomes more complicated. Suppose a new guest were to arrive, we could (simultaneously) move each guest to the next room (Room 1 into room 2, room 2 into room 3 and so on in the fashion of moving n into n+1) therefore allowing room for the new guest. In this fashion it is always possible to accommodate a finite number of guests. But what if an infinite number of guests arrived? We know that there are an infinite amount of odd numbers, so the solution to accommodating an infinite number of new guests is to move our current guests into the infinitely even numbered rooms in the process of n into 2n, which will, in turn, free up an infinite number of odd rooms.
Hilbert’s explanation of infinity opens up the, frankly odd, concept that there are many different infinities, and some are bigger than others! This is most easily demonstrated by looking at the numbers between 1 and 5 and between 1 and 10. Due to the never ending nature of our decimal system there exists an infinite amount of numbers between 1 and 10, but there also exists an infinite amount of numbers between 1 and 5 and although the latter would appear to be half as big both sets have the same cardinality due to the presence of infinity. In fact, between every number you can think of there is an infinite amount of more precise decimals, which, in turn, means there are an infinite amount of infinities!
So, a vastly complicated area. However there are many applications of this concept, especially within the areas of physics and maths (although it could also be linked with philosophy, religion and language) and although infinity might be too complicated to be introduced lower down in a school it could certainly be broached with the older children, for example, as a way to better understand the universe in which they live.