It’s that time of year again. Everything seems to be Christmas themed, and not being one to rock the boat, I think it’s time to investigate the maths behind Christmas!
Snowflakes are something which from a young age have fascinated me. Although this may have been mostly due to their unparalleled ability to form snowballs which I could throw at people. None the less, as I have stated in previous blog posts; maths is in everything. In particular I am going to discuss one snowflake. Koch’s snowflake. This snowflake is a fractal (a fractal is a shape that contains similar patterns which recur throughout the shape on a smaller scale) which is demonstrated in this video here.
As can be seen in the video, no matter how far we zoom into this snowflake there is always more detail to be revealed. An area like this, of course, opens up a variety of fundamental areas of mathematics which could be explored in the primary classroom (especially during the winter months) for example scaling, shape and ratio.
However taken a step further this simple snowflake becomes very interesting. Koch’s snowflake, as can be seen in the previously linked video is made up of triangles each a third size of the triangle it is attached to. Now, we know it to be true that no matter how far we zoom in, there will always be more detail revealed and as such we can state that to create this shape there are infinitely many triangles. Therefore we can assert that this shape has an infinite perimeter (this is because by adding up an infinite amount of triangles along its length we arrive at infinity). However Koch’s snowflake has a finite area, which can be clearly demonstrated by simply drawing a circle around the snowflake (we know the circle to have a finite area so therefore anything that can fit within the circle must have a finite area). We have now shown that the shape of a snowflake has an infinite perimeter but a finite area. Very strange!
This of course is a very abstract example of mathematics of which, unless it is actually snowing outside, the children are unlikely to find relevant and I’m sure you’re probably thinking that nothing about this idea is actually apparent in the real world. However, it is not merely just snowflakes which contain the property of infinite perimeter and finite area. Many other examples of this exists and is certainly an area that could be explored in the classroom to both find shapes that fit these rules but also why they fit these rules, which, of course, will require further exploration of fundamental mathematical ideas such as shape, ratio, division, and multiplication.
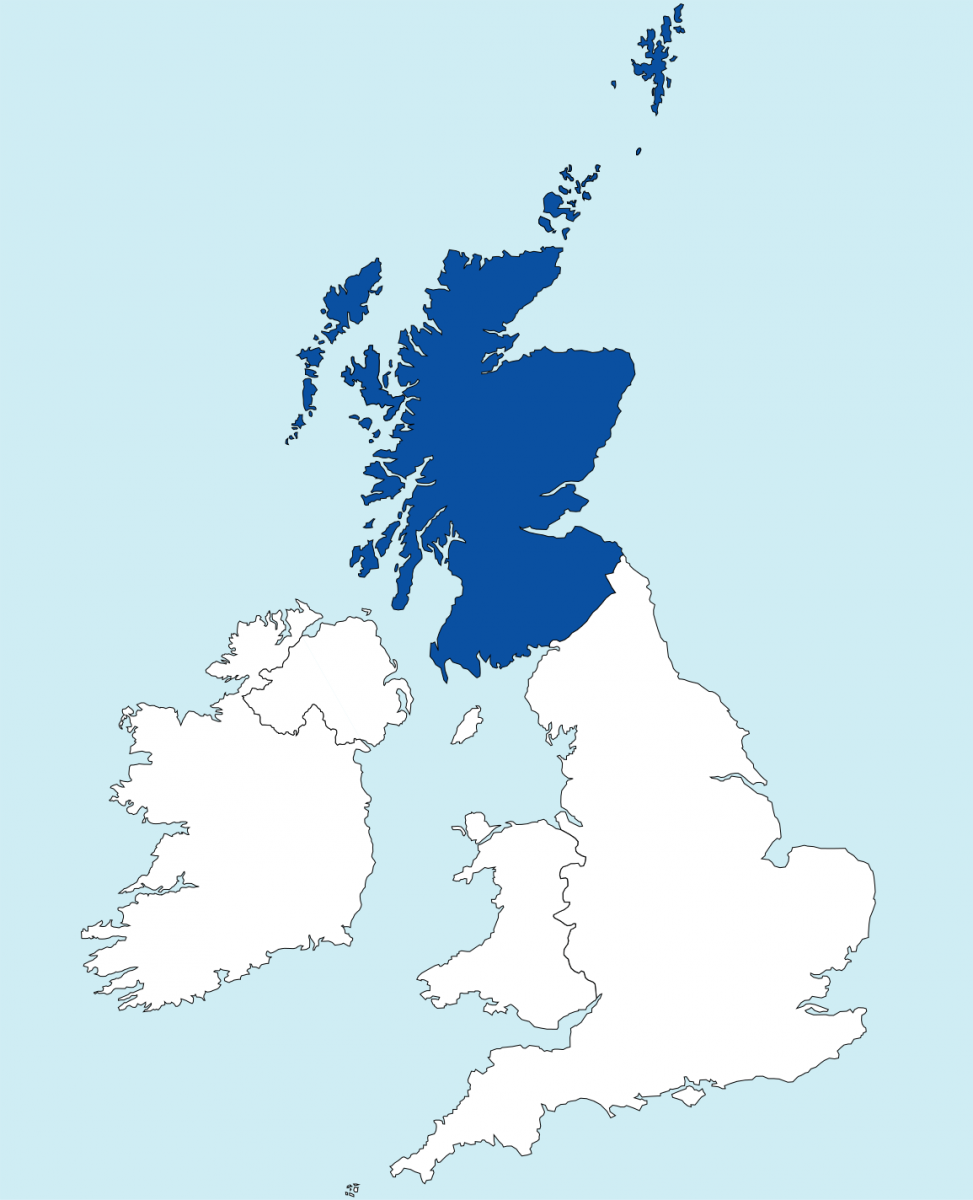
To get you started (in case it isn’t snowing when you next begin to think about fractals), despite how difficult it is for my mind to grasp the concept, Scotland is a perfect example of a shape which has an infinite perimeter but finite area.