We come into contact with numbers every day. Time, working out how many portions of dinner we’ll need to make or simply “hey what’s your number?”. But have we ever taken the time to think, what is a number and why do we even use them?
My first question is, why does the number three collectively represent other items in threes? Surely three dinosaurs would be more than three peas, even though they represent the same amount collectively. But it’s not due to weight, height or mass, its due to the value of the number three. Numbers are a language. For value, comparison and equivalence. They help us understand how many there is of something (value), help us compare that five dinosaurs are two more than three peas and that three peas and three dinosaurs are equal.
Numerals play a significant part in this. A numeral is the symbol or collection of symbols used to represent a number. A child’s first experience of a number is most likely going to be an adjective that would collectively describe a set of something e.g. five cats or two arms, this is more commonly known as the ‘cardinal aspect of a number’ (Haylock, 2014). This highlights that children can recognise an equivalence between two sets of objects and is why we understand that three dinosaurs are equal to three peas. At this stage numerals are the link to numbers. Therefore, children can look at numerals such as pictures of shapes or objects and count how many are there of one thing. This will therefore help them connect to real life situations and when shown beside numbers, they can begin to connect numerals and numbers together. By beginning to connect the two, children will have a deepened understanding of numbers and therefore their longitudinal coherence will develop. Starting their journey with numbers and maths simply and positively to prevent future maths anxiety (MA, 2010).
Numerals have been shown throughout our history and teach us a lot about the development of mathematics. One of the oldest is hieroglyphics, used by the Egyptians, dated as far back as 3000 BC. Their numerals were shown through drawings and symbols such as a bird and an Egyptian man (O’Connor and Robertson, 2000). Maths was commonly used by Egyptians if they were dividing food, solving problems for trade and market and most importantly for the pyramids (Mastin, 2010). This highlights the first use of maths for economy and trade. Wealth played a significant part in Egyptian life and social class was divided by money but more than anything, maths. Through looking at our history, we can see the similarities in the importance of economy then and now. We live in a world that’s economy changes daily and has the power to change and impact upon people’s lives. If we looked more in depth at historical economy such as Egyptian trade and social classes, we could learn and reflect on our economy nowadays and therefore maths is a historical aspect of economy that involves counting and numbers.

All factors of numbers have a place in fundamental maths, but most importantly teach us a lesson for now. We can apply what we have seen previously in history and the importance of numerals and numbers to aid our development with maths and see that it is essential for our wider society and not just basic classroom use. Relevance is a fundamental principle of Curriculum for Excellence (Scottish Government, 2010) and therefore it is important that teachers bring this forward from historical findings into our everyday maths lessons and make children think about their future with maths in society.
Number Patterns and Sequences
Another way of teaching maths can be through number patterns and sequences. This can be another way of making maths interesting for children whilst developing their relationship with numbers. Vale and Barbose (2009, p9), stated that the use of patterns in maths can challenge students to use “higher order thinking skills and emphasise exploration, investigation, conjecture and generalisation.” Therefore, basic skills in maths are used within problem solving to develop not only longitudinal coherence but also multiple perspectives as they can use different methods to find the solution to a problem.
An interesting number pattern is Pascal’s Triangle, named after Blaise Pascal, a French mathematician. This is a triangle that starts with the number ‘1’ and then below are the sum of the addition from the numbers above. For example, if 1 is beside 2 in the triangle the sum (number written below) would be 3. An example of this can be seen below.
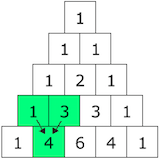
Pascal’s Triangle makes maths fun for children whilst learning about addition and number patterns. Addition is a fundamental aspect of maths that it taught as early as ages 4-5 and can be continued to be taught throughout primary school through ways such as Pascal’s Triangle. The introduction of colours can also produce other findings within the triangle. For example, pupils can colour odd and even numbers or work out the horizontal sums of the triangle (Maths is Fun, 2017). This therefore keeps maths relevant and allows for differentiation in a classroom, as some can complete the main body of the triangle (addition) and some can move forward looking at other aspects of the triangle. Therefore old maths techniques and problem solving continue to find a relevance in our everyday maths and classroom.
References:
Haylock, D. (2014) Mathematics Explained for Primary Teachers. 5th edition: SAGE.
L, Mastin. (2010) Egyptian Mathematics https://www.storyofmathematics.com/egyptian.html (Accessed: 5th October)
J, O’Connor and E, Robertson. (2000) Egyptian Numerals. http://www-history.mcs.st-andrews.ac.uk/HistTopics/Egyptian_numerals.html (Accessed: 5th October)
Ma, L. (2010) Knowing and Teaching Elementary Mathematics. (Anniversary Ed.) New York: Routledge.
N/A (2017) Pascal’s Triangle. https://www.mathsisfun.com/pascals-triangle.html (Accessed: 6th October 2018).
Scottish Government. (2010) Curriculum for Excellence Building the Curriculum 3 A Framework for Learning and Teaching: Key ideas and Priorities. Available at: http://dera.ioe.ac.uk/1240/7/0099598_Redacted.pdf (Accessed: 5th October 2018).
Vale, I. and Barbosa, A. (2009) Multiple Perspectives and Contexts in Mathematics Education. Available at: https://www.academia.edu/1485703/Patterns_multiple_perspectives_and_contexts_in_mathematics_education (Accessed: 5th October 2018).
