Category Archives: Discovering Mathematics

Map Reading. Where do I go from here?

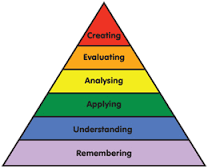
Developing map reading skills is vital within the classroom as it also develops such skills as higher order thinking skills (HOTS). HOTS is a child’s ability to reason, problem solve, judge and think critically. Understanding how to read a map gives children a better spatial reasoning, a greater understanding of the difference between 3-dimensional and 2-dimensional shapes, objects and angles.

Higher Order Thinking Skills

Despite the fact electronics have taken over from the ‘old-fashioned’ paper copy, it is still a vital skill to be able to read, follow and understand the different symbols and illustrations on a map. Even to give and receive basic directions require you to be able to have this knowledge to draw upon. Everyday situations require the understanding of map reading such as the various stops on a public transport route to ensure you get off at the correct location closest to your destination requires the understanding of maps.

This website has effective lesson ideas and concepts to teach map reading skills to children effectively: http://www.learnnc.org/lp/editions/mapping/6430

Despite the value, map reading is often not seen as a good subject to teach as many teachers fail to provide the correct lessons and support for children in their class. Many lesson plans fail to deliver the skills children require to effectively read maps. They fail to provide instruction to make clear the different attributes and qualities of a map. Children then fail to achieve the knowledge and understanding needed for these skills and additionally for the ability to transfer skills into another area.

I believe, when taught correctly, map reading skills is highly beneficial to children. It helps with their ability to analyse, reflect and problem solve. These skills can be transferred to understanding different concepts such as co-ordinates, spatial awareness and graphs. I credit the implementation of new technology and programs which ease the effort and knowledge required to get to an unknown location but i believe these fundamental skills are still vital to a person’s welfare.

Fibonacci sequence

Leave a reply

Fibonacci sequence 0,1,1,2,3,5,8,13,21,34,55,89,144…

The Fibonacci sequence is extraordinarily interesting. It is surprisingly in so many things around us. Like the staggered pattern of certain plants’ leaves to optimise the absorption of sunlight so it hits every leaf. The golden ratio (https://en.wikipedia.org/wiki/Golden_ratio) is present in the angles between each leaf so it perfectly separates them to prevent as much overlap as possible.

If you take a look at the nearest plant to you, how many leaves does it have? When you count them in spirals they may begin to reflect the Fibonacci sequence and spiral. This isn’t easy to do on many plants (evident below) and it may not be possible on certain ones. There are always exceptions to the rule. But maybe these aren’t exceptions but instead they have their own rules…

It’s also in many plants and therefore fruit such as pinecones and pineapples. Wait, there’s a common theme there. Pine. Pine comes from the root *peie meaning “to be fat, swell”. Could this relate to the Fibonacci spiral which grows you could even say it somewhat swells.

The pineapple shows the fibonacci sequence as they possess the fibonacci spirals and also have the fibonacci sequence shown in the number of sections there are.

Pineapple showing the Fibonacci sequence

Through this we see that the fibonacci sequence is all around us from sunflowers to the curves of waves, we just need to look for them.

Happy Birthday to… us?

Leave a reply

Birthday Probability

In this video Sal explains why there is a high probability that 2 people in a room of 30 (which is a potential size of a classroom) may share a birthday. He explains the pattern created by the calculations which find the probable percent of 2 or potentially more people in a room with the same birthday.

He considers the 365 days in a year that person 1 could be born on which is 1. Person 2 would therefore only has 364 possible days for a different birthday. That pattern would continue eg. person 3 – 363 days, person 4 – 362 days, person 5 – 361 days etc.

Sal states that, since this is only for 30 people, the number of days of each of the 30 people get multiplied over the number of days in the year (365) to the power of 30 as that’s how many people there are.

But that gives us the probability that no one would share a birthday so he shows it more simply with factorials which is also much easier to type into a calculator.

It can be written as 365!/(365-30)! = .2937 therefore equaling a 29.37% probability that no one in the class shares a birthday.

So… the probability that 2 or more people in a room of 30 is all the people minus the probability that no one shares a birthday which is 100% – 29.37% = 70.63%

In a room of 30 people there is a 70.63% chance 2 people share a birthday

I believe it is an interesting concept to teach children. It would provide them with the ability to connect the notion of patterns throughout mathematics and link it to other areas to gain a greater understanding. Other skills are also gained through doing this such as calculator skills, the use of percentages and basic arithmetic. Mathematics is connected in many ways and these skills can be transferred to other areas.

Tessellation

Leave a reply

Tessellation involves tiling using geometric shapes. These shapes are ones which, when replicated and placed next to each other, have no spaces or overlaps between them. The geometric shapes used must be regular polygons meaning all the angles are of the same degrees and the sides must be of the same length. These include: squares, hexagons and equilateral triangles.

Where three of the regular polygons vertices meet, they form 360°. As the vertex of:

A square is 90° therefore 90° x 4 = 360° hence four squares would tessellate

An equilateral triangle is 60° therefore 60° x 6 = 360° hence six equilateral triangle would tessellate.

A hexagon is 120° therefore 120° x 3 = 360° hence three hexagons would tessellate.

Any shapes with 4 sides (quadrilaterals) can tessellate as where the vertices meet it must equal 360°. Hence, Vertex A + Vertex B + Vertex C + Vertex D = 360°. Therefore it is proven that any quadrilaterals can be repeated allowing them to tessellate.

The tiling of irregular shapes without any gaps or overlap can also produce tessellation. To create tessellated patterns three techniques are used, rotation, reflection, translation. Here is an example I made:

Tessellation like many other mathematical skills and concepts are an art. M. C. Esher used tessellation and other geometric patterns and distortions in his art.

Welcome to Discovering Mathematics

Leave a reply

The fear of maths is something which is in many people, but maths is something which is in our entire world. Whether we wish to accept it or not, maths is all around us. It is in the architecture around us, the baking we love to smell and even in the shells found on the sandy beaches. Through counting, shapes, patterns and many more skills we can explore maths. Maths is fun. Here I will blog about my learning and reflections on the very fascinating subject of maths.