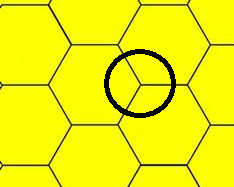
Tessellation involves tiling using geometric shapes. These shapes are ones which, when replicated and placed next to each other, have no spaces or overlaps between them. The geometric shapes used must be regular polygons meaning all the angles are of the same degrees and the sides must be of the same length. These include: squares, hexagons and equilateral triangles.
Where three of the regular polygons vertices meet, they form 360°. As the vertex of:

An equilateral triangle is 60° therefore 60° x 6 = 360° hence six equilateral triangle would tessellate.
Any shapes with 4 sides (quadrilaterals) can tessellate as where the vertices meet it must equal 360°. Hence, Vertex A + Vertex B + Vertex C + Vertex D = 360°. Therefore it is proven that any quadrilaterals can be repeated allowing them to tessellate.
The tiling of irregular shapes without any gaps or overlap can also produce tessellation. To create tessellated patterns three techniques are used, rotation, reflection, translation. Here is an example I made:

Tessellation like many other mathematical skills and concepts are an art. M. C. Esher used tessellation and other geometric patterns and distortions in his art.