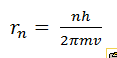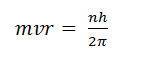Quantum Physics

 

1.(a) Explain qualitatively how the Bohr Model of the atom can account for line emission spectra.

 

(b) It is possible to calculate a de Broglie wavelength for a moving object.

 

A ball of mass 45g has a speed of 68ms^-1.

 

(I) Calculate the de Broglie wavelength for the ball.

 

(ii) Explain why wave-like properties are not observed for the ball.

 

2. (a) State what is meant by the Uncertainty Principle in relation to the position and momentum of a subatomic particle.

 

(b) An athlete has a mass of 70 kg. At the finish line the position of the athlete has an uncertainty of 1.0 x 10^-3 m. Calculate the minimum uncertainty in the momentum of the athlete at the finish line.

 

(c) It takes about 1.6 X 10^-13 J of energy to create an electron-positron pair.

For what approximate period of time can this amount of energy be borrowed before it has to be paid back by electron-positron annihilation?

 

3. (a) Bohr’s model of the hydrogen atom includes assumptions about the orbiting electron. One of these is that the electron moves in a circular orbit centred on the nucleus.

 

(j) State briefly one of the other assumptions.

 

(ii) By considering the electron as a point mass m travelling around the nucleus, show that the radii of the allowed orbits r_n are given by

where the symbols have their usual meanings.

 

(iii) Calculate the speed of an electron in the first allowed orbit of radius 5.3 x 10^-11 m.

 

(b) Planck and Einstein suggested that electromagnetic radiation exhibits a wave-particle duality. De Broglie extended this idea to matter.

 

(i) Write down an expression for the wavelength λ associated with a particle that has a momentum of magnitude p.

 

(ii) (A) A woman of mass 50kg walks through a doorway at a speed of 1.5 ms^-1. Calculate her de Broglie wavelength.

 

(B) Explain why the effect of diffraction is negligible when the woman passes through the doorway.

 

4. (a) Electrons can exhibit wave-like behaviour. Give one example of evidence which supports this statement.

 

(b) The Bohr model of the hydrogen atom suggests a nucleus with an electron occupying one of a series of stable orbits.

 

A nucleus and the first two stable orbits are shown below.

(i) Calculate the angular momentum of the electron in the second stable orbit.

 

(ii) Starting with the relationship

show that the circumference of the second stable orbit is equal to two electron wavelengths.

 

(iii) The circumference of the second stable orbit is 1.3 x 10^-9 m. Calculate the speed of the electron in this orbit.