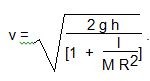1 A flywheel has a moment of inertia of 1.2 kgm2 . The flywheel is acted on by a torque of magnitude 0.80 N m.
(a) Calculate the angular acceleration produced.
(b) The torque acts for 5.0 s and the flywheel starts from rest. Calculate the angular velocity at the end of the 5.0 s.
2 A mass of 0.10 kg is hung from the axle of a flywheel as shown below. The mass is released from a height of 2.0 m above ground level.
The following results were obtained in the experiment:
time for mass to fall to the ground t = 8.0 s
radius of axle R = 0.10 m.
(a) By energy considerations, show that, ignoring friction, the final speed of the flywheel is given by ![]() where I is the moment of inertia of the flywheel.
where I is the moment of inertia of the flywheel.
(b) Calculate the moment of inertia of the flywheel.
3 A heavy drum has a moment of inertia of 2.0 kg m2. It is rotating freely at 10 revs-1 and has a radius of 0.50 m. A constant frictional force of 5.0 N is then exerted at the rim of the drum.
(a) Calculate the time taken for the drum to come to rest.
(b) Calculate the angular displacement in this time.
(c) Hence calculate the heat generated in the braking action.
4 A cycle wheel is mounted so that it can rotate horizontally as shown.
Data on wheel: radius of wheel = 0.50 m, mass of wheel = 2.0 kg.
(a) Calculate the moment of inertia of the wheel system. State any assumptions you make.
(b) A constant driving force of 20 N is applied to the rim of the wheel.
(i) Calculate the magnitude of the driving torque on the wheel.
(ii) Calculate the angular acceleration of the wheel.
(c) After a period of 5.0 s, calculate:
(i) the angular displacement,
(ii) the angular momentum of the wheel, and
(iii) the kinetic energy of the wheel.
5 A very light but strong disc is mounted on a free turning bearing as shown below.
A mass of 0.20 kg is placed at a radius of 0.40 m and the arrangement is set rotating at 1.0 revs-1 . (The moment of inertia of the disc can be considered to be negligible.)
(a) Calculate the angular momentum of the 0.20 kg mass.
(b) Calculate the kinetic energy of the mass.
(c) The mass is pushed quickly into a radius of 0.20 m.
By applying the principle of conservation of angular momentum, calculate the new angular velocity of the mass in rads-1 .
(d) Find the new kinetic energy of the mass and account for any difference.
6 A uniform metal rod has a mass, M, of 1.2 kg and a length, L, of 1.0 m. Clamped to each end of the rod is a mass of 0.50 kg as shown below.
(a) Calculate an approximate value for the moment of inertia of the complete arrangement about the central axis as shown. Assume that Irod = ML²/12 about this axis.
(b) The arrangement is set rotating by a force of 10 N as shown in the diagram. The force acts at a tangent to the radius.
(i) Calculate the applied torque.
(ii) Hence find the maximum angular acceleration. You may assume that the force of friction is negligible.
(iii) Calculate the kinetic energy of the arrangement 4.0 s after it is set rotating.
7 An unloaded flywheel, which has a moment of inertia of 1.5 kgm², is driven by an electric motor. The flywheel is rotating with a constant angular velocity of 52 rads-1. The driving torque, of 7.7 N m, supplied by the motor is now removed.
How long will it take for the flywheel to come to rest. You may assume that the frictional torque remains constant?
8 A solid aluminium cylinder and a hollow steel cylinder have the same mass and radius. The two cylinders are released together at the top of a slope.
(a) Which of the two cylinders will reach the bottom first?
(b) Explain your answer to part (a).
9 A solid cylinder and a hollow cylinder each having the same mass M and same outer radius R, are released at the same instant at the top of a slope 2.0 m long as shown below. The height of the slope is 0.04 m.
M = 10 kg, R = 0.10 m M = 10 kg, R = 0.10 m, r = 0.05 m
I = MR²/2 I = M(R² + r²)/2
It is observed that one of the cylinders reaches the bottom of the slope before the other.
(a) Using the expressions given above, show that the moments of inertia for the cylinders are as follows:
(i) solid cylinder; I = 0.05 kgm² (ii) hollow cylinder; I = 0.0625 kgm².
(b) By energy considerations, show that the linear velocity of any cylinder at the bottom of the slope is given by:
(c) Using the expression in (b) above, calculate the velocities of the two cylinders at the bottom of the slope and hence show that one of the cylinders arrives at the bottom of the slope 0.23 s ahead of the other.