Torque and moment of inertia
- (a) State what is meant by the moment of a force.
(b) Give two examples illustrating the moment of a force.
- (a) State the equation between torque and tangential force.
(b) State the equation between torque and angular acceleration.
- The moment of inertia of an object depends on two quantities. State clearly the two quantities concerned.
- The moment of inertia of a rod about an axis through its centre is different to the moment of inertia of the same rod about an axis through one end. Explain why this is so and justify which arrangement has the larger moment of inertia.
- A wheel has very light spokes. The mass of the rim and tyre is 2.0 kg and the radius of the wheel is 0.80 m. Calculate the moment of inertia of the wheel. State any assumptions that you have made.
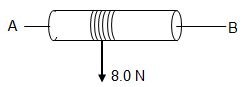
- A cylindrical solid drum is free to rotate about an axis AB as shown below.
The radius of the drum is 0.30 m. The moment of inertia of the drum about AB is 0.40 kgm2. A rope of length 5.0 m is wound round the drum and pulled with a constant force of 8.0 N.
(a) Calculate the torque on the drum.
(b) Determine the angular acceleration of the drum.
(c) Calculate the angular velocity of the drum just as the rope leaves the drum. You may assume that the drum starts from rest.
- A hoop has a radius of 0.20 m and a mass of 0.25 kg.
(a) What is the moment of inertia of the hoop?
(b) What torque is required to give the hoop an acceleration of 5.0 rads-2?
- A sphere has a moment of inertia of 0.40 MR2 where M is the total mass of the sphere and R is the radius.
(a) Calculate the moment of inertia of the Earth as it spins on its axis. State any assumptions made.
(b) What is the tangential speed at the surface of the Earth at the Equator?
- Two children are playing on a roundabout. One child, Anne, of mass 50 kg, stands on the roundabout 1.25 m from the axis of rotation. The other child, Robert, starts the roundabout by applying a constant torque of 200 N m at the rim for 3 s. When rotating there is a constant frictional torque of 25 N m acting on the roundabout. Robert stops pushing and the roundabout comes to rest. The moment of inertia of the roundabout alone is 500 kgm2.
(a) Calculate the maximum angular velocity of the roundabout.
(b) Find the time taken for the roundabout to come to rest.