What is ‘Connectedness’?
Connectedness within mathematics is where each concept is linked to a number of other concepts. Liping Ma (2010) describes how a teacher who does use connectedness to teach a mathematical topic may teach it as a ‘stand-alone’ topic, not linking it to anything else in the curriculum or what the children have learned before. Teachers with using connectedness do not just focus on one particular part of mathematics, they draw from a “knowledge package” they have developed through their own learning. This means that when a teacher uses connectedness in their teaching, they will not only have an idea of the concept to be taught, but also all of the interlinking concepts relating to it.
This is connectedness…
If you’d like to see a bigger picture – have a look here.
But what is it connecting? Galaxies? Pathways in the brain? Let’s have a look…
It’s connecting all the different concepts of the GCSE maths curriculum together to demonstrate exactly how interlinked they all are. The larger the word the more that maths it is used in the classroom.
Each dot represents a maths topic. There are 164 spots on the diagram representing all topics in the curriculum. The spots are connected by 935 which represents a connection between two topics where one topic must be learned before the other can be taught. For example, you must learn how to add fractions before you can learn how to do equivalent fractions.
The size of the spot represents how many links they have and therefore how many topics rely on them for prior learning. The larger the spot the more topics rely on it. Therefore largest spots represent the fundamental maths skills required to be able to fully understand all parts of GCSE maths.
The colour of each spot represents the part of the curriculum they relate to:
Number and calculating – red, Shape space and measure – purple, Algebra- turquoise, Data handling and probability- light green
Click here to download a high-resolution pdf of the network diagram.
The largest spots are red showing that if the number topics have not been mastered you will struggle to teach them much else. If you removed all the red nodes, and those they are connected to, you would have little left that you could teach.
Let’s compare this to a linear way of teaching maths…
(Source: http://www.beaumontleys.leicester.sch.uk/maths/)
Using the timetable above as an example (I am in no way implying that the timetable above has been taught with no connections!) we can see if the children were taught in a linear fashion and told “today we are learning about co-ordinates”, then the next lesson “today we are learning about the properties of 3D shapes” then the children may never understand the links between all topics, so therefore not have any depth to the understanding they do have.
I feel the diagram of connectedness shows how important it is to ensure firm mathematical foundations are built during maths lessons, and that these are revisited and reinforced regularly to allow for a secure base for further knowledge to be built on and connected to. You could teach 164 stand alone topics with no links between them, or, you could teach with connectedness giving the children a firm foundation of maths whilst allowing them to create links themselves and understand how it all links together.
(Source: Great Maths Teaching Ideas. Available at: http://www.greatmathsteachingideas.com/2014/01/05/youve-never-seen-the-gcse-maths-curriculum-like-this-before/)
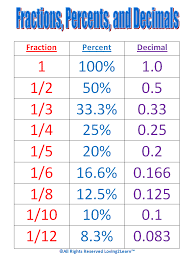
How can we use connectedness to get a bargain?
Imagine, you are in the supermarket and wanting to buy orange juice. There are three different brands of orange juice for sale and they are all on special offer. The bottles are all 1 litre and all three brands usually cost £2.50 for a bottle. However, today bottle ‘A’ has 25% off, bottle ‘B’ has 1/3 off and bottle ‘C’ has an extra 0.25ml bottle free (let’s call this 0.25 free). The question is – which one is better value, per ml of orange juice, to buy? If you did not know that fractions, percentages and decimals were connected then you couldn’t use proportional reasoning to solve the problem. This could have a negative impact on your budgeting and bank balance. So, it just goes to show that connectedness can help you get a bargain!