What is a Real Number

• Integer = whole number 

       1, 4, 67, 1234, 134567, -12

• Real Number = Decimal numbers

      1.25, 158.54, 7895.36, -45.56

Representing Real Numbers 

• Real numbers always contain a decimal point (.)
• But – the decimal point (.) cannot be stored in binary!
• However, if we can represent a real number with the decimal point always in the same place then we don’t need to store the decimal point!

Fortunately such a system exists!

SCIENTIFIC NOTATION

Examples:

123456.7        =    0.1234567 x 106

0.001234        =    0.1234 x 10-2

1234.567        =    0.1234567 x 104

All real numbers can be written in this common and consistent format

Real numbers are always stored in two parts:

• The first part holds the mantissa converted into binary
• The second part holds the exponent also converted into binary

The mantissa is the actual digits of the numbers, this is the size of the number 

The exponent is the power to which the base is raised, this stores the number of places to move the decimal point

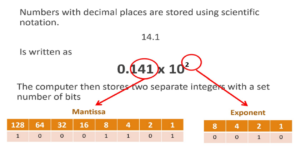
Changing the number of bits used to hold the mantissa or the exponent affects the number.

• Increasing the number of bits used for the mantissa increases the accuracy to which the number is stored
• Increasing the number of bits used for the exponent increases the range of numbers that can be stored