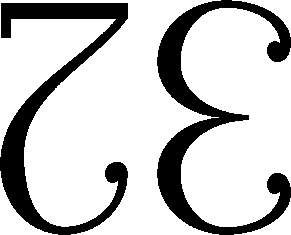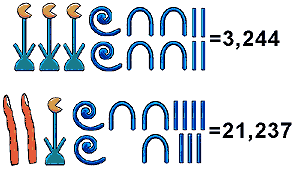From the title, it would be understandable for you to think I had gone mad. In fact, quite the opposite. I had a wonderful lesson today exploring the joys of number systems and place value.  Although at first it was not as clear, it was exciting watching the numbers evolve and make sense in front of my very eyes.

The first thing that struck me about the lesson was looking at a counting system used by shepherds when counting their sheep in medieval times:

This system uses a base 20 system, where when the shepherd counted 20 sheep, they would put a stone in their pocket to signify 20. They would then start again until they again reached 20 (40 total) and another stone in the pocket, and so on.

You can see a degree of repetition in this system with 11 (Yan-a-dik) literally standing for one and ten. However, what perplexes me is why they have tags for numbers 6 through 9, as in their system they do not seem to be used again. They have no need to have numbers beyond twenty, as after this they begin again, so why not make 6 “Yan-a-pimp”? This seems, to me, a flaw in their system, which otherwise seems to be a sensible system for them.

As I had previously read about this system before the lesson, seeing it come up automatically hooked me. This I can relate back to the classroom, as if children, like I did, recognise what they are being taught, they will associate with it much better, and I believe will be more likely to take the information on board. I think this links to Liping Ma’s idea of ‘interconnectedness’ (p122) (Ma 2010) as relating new learning to what the children already know is likely to engage them and make them eager to learn.

My excitement grew when we were then told that “Yan Tan Tethera” was the name of a Scottish Country Dance and the crib (instructions) was put on the screen, almost like a foreign language to everyone else, but looked so familiar to me. It gave me a sense of homely warmth, that I can only imagine children feel when they recognise what is on the screen in front of them. This again links back to the idea that children are more likely to be engaged in the learning if they can relate to it. For example, talking about farming to children in the inner city will not resonate with them. I am hoping to try this dance out in my dancing group and will update my blog with it soon.

 

To us using base 10, or decimal, the idea of any other base system seems alien to us. The most common base system to us, apart from base 10, is binary. Binary is a base 2 system used by computers consisting of only two digits – either a 0 or a 1. Having done Standard Grade Computing, I am fairly familiar with how binary works and how you can make any number using this system. The way I know how to use binary is using a place value system, doubling the numbers each time. This is because in base 10 system you have place values of ones, tens, hundreds etc, where the columns are 10x as much. Because it is only a base two system, the numbers only double each time. There are some examples of binary below:

16+4 = 20

32+16+4+2+1 = 55

64+4+1 = 69

By adding up all of the numbers with a one in that column, you can work out what number the binary represents.

With this idea in mind, it makes looking at other base systems much easier. For example, we then looked at base 12 systems, which is thought by many to be a more appropriate base system than base 10. Base 12 includes 2 extra single digits to replace what we know as ten and eleven (respectively shown in the picture left). These extra numerals are needed as the numeral “10” uses two columns. In the base 12 system there is a “12” column rather than a “10” column.  The video below explains this very well, however, instead of these digits above, she is using T and E to represent ten and eleven.

As you can see above, decimal columns are multiplied by 10 each time, and binary numbers are multiplied by 2. This then translates to dozenal numbers  being multiplied by 12 each time, as you can see here.

There are some who have suggested that a base 12 system would make more sense, especially in terms of looking at fractions like 1/3 and 1/4, which are not as neat in decimal. This moves on to the fact that 12 is divisible by more numbers than 10 (1,2,3,4,6,12 rather than 1,2,5,10). 12 is a fairly common number in terms of maths, looking at time especially.

Note: these clocks are commercially available.

In conclusion, this is a confusing topic to get your head around, which is exactly what some children may feel when faced with what is difficult to them. It is important that we give children the chance to play with and explore the numbers, as we were given the chance to do, which really helped me understand the topic. Children should, in my opinion, be supported, but should be encouraged to be explorers in order for them to feel the sheer joy of what maths truly is.

 

References

Ma, L. (2010) Knowing and Teaching Elementary Mathematics. (Anniversary edn). Routledge. Oxon.

Years ago, there were no numerals. No names to define amounts. This is because it simply wasn’t necessary until people began forming villages and such where numbers and numerals were needed as a means of comparison for trading. This in itself is difficult for us to imagine, growing up counting in an Arabic (sometimes known as Hindu Arabic or European) number system, with numerals 1, 2, 3, 4 etc. I should point out that there is a distinct difference between numerals and numbers.

Numerals – symbols we use to denote an amount i.e. when we use “6” , that is a numeral

Numbers – a quantity or measure of amount

Breaking this down further, there are digits. Digits are like the letters of maths – the single digits that make up a numeral. Maths is Fun shows this perfectly (link at bottom of blog):

Numerals are what we use to talk or write about amounts, whereas numbers are the idea that exists in our heads about quantity.

Our Arabic number system developed in India, as the video below shows:

Most languages today use these numerals, however, this was not always the case. The first number system was the Babylonian system in Mesopotamia, using not a base 10 system, but a base 60 system (however, there are elements of base 10 as the system uses the symbols in a tens and units format). Many early numerals are more like symbols to us, just as our numerals would be to the Babylonians – it is simply a case of what you know and what you are familiar with.

Even Roman Numerals, which we are more familiar with, are letter/symbol based. There are two theories about the origins of Roman Numerals (link at bottom). The first is based on hand gestures, just as children count on their fingers now (10 fingers = our base 10 system).

For example, 5 = V. The hand gesture is this (similar to a V):

 

10 = X. The hand gesture is this (a cross with the thumbs or hands):

The second theory is based on tally marks on tally sticks – a system used long before the Romans, especially by shepherds counting their sheep.

This same site also alludes to earlier number systems such as the Egyptian system. This is similar in ways, with a single line representing “one” however, they used lines for all digits up to “nine”, and pictures beyond these. An example of larger numbers is shown below (both pictures from Discovering Egypt website).

 

It is clear that there are many other number systems other than our own that have been used throughout history, and even today in Chinese and Japanese languages. I personally have found these fascinating to look at and I believe children would find this interesting too, looking at the unknown and how it relates to the obvious that we see and use every day. This study into different number systems all looks towards Liping Ma’s relational understanding. I would not teach these systems while children are still learning their first numerals (1, 2, 3 etc) but it would be an interesting activity with older children, showing them why we have the numerals we do, and where they came from. The activity we did this morning, creating our own number system (see my attempt on the right) was a thought provoking one. You grow up only knowing the Arabic numerals, that creating foreign ones is strange and alien. I think children would learn a lot from this type of activity, not just about number systems, but about how numbers are formed, written and constructed. Like I say, this is not an activity for early years children beginning their maths journey, but for children who are comfortable with the numbers they know and can be stretched further.

References:

Pierce, R.  (2015) ‘Numbers, Numerals and Digits‘. Math Is Fun. Available at: http://www.mathsisfun.com/numbers/numbers-numerals-digits.html (Accessed 3/10/16)

Roman Numerals and Roman Numbers (no date) Available at: http://www.knowtheromans.co.uk/Categories/SubCatagories/RomanNumerals/#VIII (Accessed 3/10/16)