Introduction

Before this input, I knew there was a huge amount of maths involved in computer games. However, I hadn’t  given this much thought as I assumed this was far beyond anything I would be able to understand with my knowledge of maths. So my question is: which elements of fundamental mathematics do I need to  help to understand complex mathematics used in computer games?

Counting

Number systems and counting are of clear importance when it comes to computer games. I have a deeper understanding of this based on previous experiences in this module. We learned that base twenty system was used for counting due to having ten fingers and ten toes. Learning of the Mayan’s using a base twenty number system encouraged me to think of the differences made when the base is changed. Lumen (undated) states ‘the Mayans used a base-20 system, called the “vigesimal” system. Like our system, it is positional, meaning that the position of a numeric symbol indicates its place value’. This means that a base twenty number system is also positional in the same way that our base ten system is.

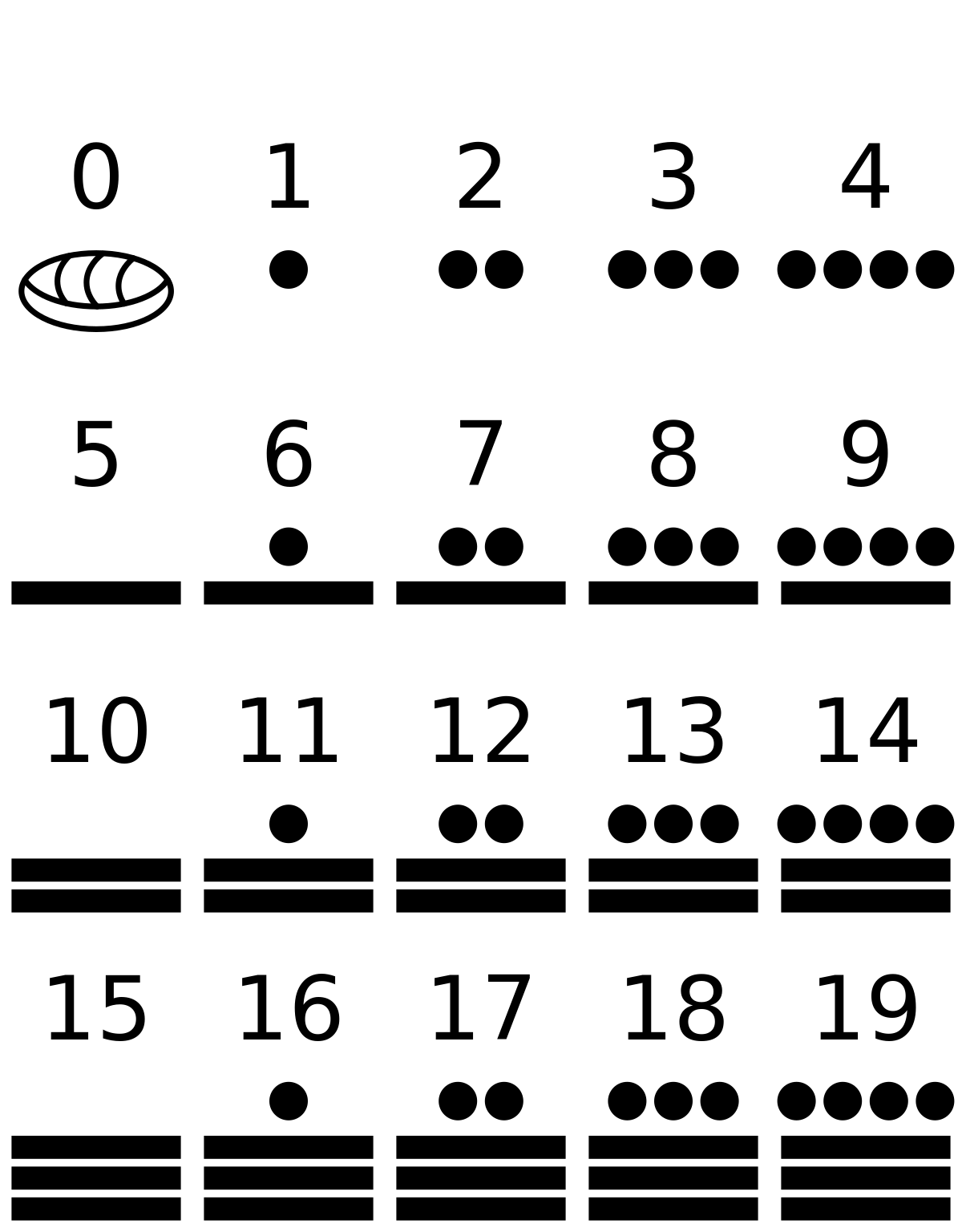
Although I do understand what base ten number system is, I decided to explore it further to deepen my understanding. Killian (2012a) states ‘the process repeats over and over, and eventually you get to 99, where you can’t make any larger numbers with two digits, so you add another, giving you 100’. So if this explains the system when counting, what happens when it comes to large numbers? Smith and LeVeque (undated) state ‘when it became necessary to count frequently to numbers larger than 10 or so, the numeration had to be systematized and simplified; this was commonly done through use of a group unit or base’. Therefore, as maths grew more complicated, our number system had to be adapted to become easier to work with.

Binary

Computers use a base two number system as they work in a different way but an understanding of number systems allows for understanding this process to become much easier. Killian (2012b) states ‘ while everyone knows binary is made up of 0s and 1s, it is important to understand that it is no different mathematically than any other base’. This made the idea of binary seem more approachable as someone who has no previous knowledge on the subject. I had a grasp of the concept of binary but in order to have a thorough understanding I looked into comparing binary to our number system.

Therefore, binary operates on a very small base 2 number system, this means that computers can only tell if a wire is on or off. Binary also operates in eights which makes the process much clearer to me. This has simplified for me a process which I previously thought would be highly complicated. This has highlighted for me the importance of independent research in order to deepen my understanding. With a better knowledge I will feel less intimidated when exploring different and interesting areas where maths can be applied with my pupils.

Now that I have this knowledge, I will be able to provide a much richer experience in practice. On my first placement, the pupils were using a programme called ‘Scratch’ in their ICT lessons. I saw the basic idea that they were programming their own games but did not understand much deeper than this. I feel that now I would be able to provide sufficient explanations and make connections with maths in ICT which could bring this to life.

Conclusion

Therefore, the list of mathematical processes involved in computer games is endless. However, a huge part of this is number, number systems and place values. Having an understanding of this can simplify understanding a topic which may otherwise seem too complex. I think that if pupils if teachers can explain the maths behind a topic such as computer games, they will be more engaged and motivated.

References

Killian, J. (2012). ‘Number Systems: An Introduction to Binary, Hexadecimal, and More’. Available at: https://code.tutsplus.com/articles/number-systems-an-introduction-to-binary-hexadecimal-and-more–active-10848. (Accessed: 9/11/18).

Lumen (undated). ‘The Mayan Numeral System: Mathematics for the Liberal Arts’. Available at: https://courses.lumenlearning.com/waymakermath4libarts/chapter/the-mayan-numeral-system/. (Accessed: 9/11/18).

Smith, E, D, LeVeque, J,W. (2012). ‘Numerals and numeral systems’. Available at: https://www.britannica.com/science/numeral. (Accessed: 9/11/18).

Images

https://en.wikipedia.org/wiki/Maya_numerals

https://scratch.mit.edu/

Introduction

The concept of taking learning outdoor is something I am familiar with. However, I would associate this with subject such as language, gym or science. I have given a lot of thought to thinking beyond the classroom in maths but i had not considered the benefits of physically taking maths outside. So my question for this post is, which elements of fundamental mathematics can be developed effectively outdoors?

Angles

After doing some research and thinking back to my first placement, measurement and angles stood out in particular. There are multiple ways to include variation in the teaching of angles within the classroom. However, it is important to think creatively, something I have discovered in previous posts. Haylock (2007, p. 266) explains that ‘when teaching about angles, do not always draw diagrams or give examples in which one of the lines is horizontal’. This further explains this idea that angle should be taught in a multitude of ways.

I also think that this can be related to one of the CfE defined principles of relevance, Scottish Government (2017). If children are only calculating angles in a textbook, they may struggle to see the relevance of angle in the real world.

Measurement 

The points made are similar when it comes to measurement, creative teaching is also key. Hansen (2006, p. 104) states ‘children begin to form an idea naut length when objects can be matched and compared’. This will be far easier to do if children can compare and contrast different objects or buildings outside. An example of this on my first placement was when the pupils went outside to calculate the perimeter of the school. This brought their previous learning to life.

Outdoor Learning

Outdoor learning can be an effective means of teaching maths. NCTEM (2015) states ‘getting out of the classroom facilitates authentic or experiential learning (the engagement of learners with the world as they actually experience it)’. Throughout this module I have realised the importance of valuable experiences in maths. Therefore as a teacher it is important to enrich the pupils learning by providing experiences such as fun outdoor lessons. A change of environment could also be refreshing for the class. Maynard and Waters (2007, p.260) states ‘while the teachers indicated that they were unsure whether or not they should change their pedagogical approach when working outside, several indicated that they felt more relaxed outdoors’. Therefore being outside could be a nice change from learning in the classroom. I  have also considered maths anxiety a lot throughout this module and learning outdoors could be a means of creating a more relaxed and positive attitude towards maths. Pupils could begin to see the real life maths and have less anxiety out with the confines of the classroom.

It is particularly important to make use of the materials outside, as opposed to conducting a lesson created for indoors outside. Bilton (2010, p. 4)  ‘quality outdoor provision would incorporate this type of practice, but merely taking indoor equipment outside does not constitute quality outdoor provision’. This could be implemented by basing the lesson on objects outdoors or buildings. For example calculating the diameter of a tree or perimeter of a building. This could also involve using materials found outside, this will encourage pupils to discover for themselves and find innovative ways to use maths outside.

Conclusion

Therefore, angles and measurement are key fundamental maths skills that can be explored outdoors. However, materials outdoors can be used to create lessons in any area of mathematics. This can bring a change of scenery for peoples which could engage and motivate them. It will also highlight the relevance by bringing mathematics out of the classroom and making fun activities outdoors.

References

https://www.tts-group.co.uk/maths-outdoor-grab-and-go-foundation-kit/1002001.html

Introduction

When I think of learning about probability, all I remember is discussing the chances of rolling each number on a dice. Although this is an effective way to teach probability, my question for this week is: what are the methods that can be used to teach probability?

Gambling

I knew that gambling was all about statistics but I had not considered the fact that games in casinos are probability on a large scale. Akusobi (2010) states ‘all events in gambling games have absolute probabilities that depend on sample spaces, or the total number of possible outcomes’. This means that professional gamblers constantly asses the risk and chances of certain outcomes. This highlighted for me an application of probability that is widely used in casinos all over the world.

A game such as roulette has an element of subjective probability. Investopedia (undated) states ‘it contains no formal calculations and only reflects the subject’s opinions and past experience’. For example, if it has landed on black six times in a row, a person may take the subjective probability approach and assume it will land on red next. This is based on the past experience of several of the same colour in a row. There would be no calculations in this, instead it is a logical assumption. Looking into the mathematics behind gambling brought forward the relevance and applications for me. I think that it is therefore important to make it relevant for the pupils I will teach.

Tossing a Coin

We experimented with tossing a coin in class to explore the probability. We first wrote down our predicted results without tossing a coin and then compared this with results when using a coin. We found that nobody had written the same outcome more than five times in a row. I think this was an example of us applying subjective probability. We all assumed that the chances of the same outcome appearing several times in a row was small. This is because we know that there are only two outcomes and would assume that the number of times for each outcome would be relatively equal. McCluskey and Lalkhen (2017) further explain ‘common sense tell us that, provided the coin is unbiased with heads just as likely to fall as tails, the ratio of heads:tails should be 1:1 and therefore the ‘expected’ outcome after 20 tosses would be 10 heads’. This confirms this idea that we all made an assumption based on the probability that we thought was most likely using common sense.

Rolling a Dice

Starting with the most common example when teaching probability, the dice. Probability is the chance or something happening and in this case, what the chances are of rolling each number. BBC (undated) states ‘there is one way of rolling a 4 and there are six possible outcomes, so the probability of rolling a 4 on a dice is 1/6. This is called the ‘theoretical probability’ – in theory, if you roll a dice six times then you should roll a 4 once’. It is therefore important to highlight to pupils that this is simply a theoretical probability. However, I think that of we were to explain this to pupils, they may not fully understand. I think it is important to let pupils explore and discover this theoretical probability for themselves. For example, rolling a dice for themselves and recording results. Exploring this concept independently will give the pupils a more thorough understanding of probability.

Terms

Now that my own knowledge of probability is better, I have realised the concept does not need to be taught in isolation. I think it could be effective to teach probability within other activities. For example, when the pupils are playing games. The pupils could explore what the odds are of winning or losing. This could promote discussion about maths. Pupils should first have an understanding of the terms. MCA Online (2017) explains the terms as impossible, unlikely, even chance, likely and certain. I think it would be effective to encourage pupils to identify the probability of different situations using these terms. This will encourage a consideration of the application of probability in daily life.

Conclusion

Therefore, my experience of learning about probability made it a far more interesting concept for me. It has also allowed me to see the applications of it elsewhere. This means that I have a much deeper understanding of the topic. This has also shown me that I must provide the same experience for pupils. They should also have the opportunity to learn in interesting and engaging ways in order to build a positive relationship with mathematics.

References

Akusobi, C. (2010). ‘Should You Bet On It? The Mathematics of Gambling’. Available at: http://www.yalescientific.org/2010/02/should-you-bet-on-it-the-mathematics-of-gambling/. (Accessed: 30/10/18).

BBC (undated). ‘Probability’. Available at: https://www.bbc.com/bitesize/guides/zsrq6yc/revision/2. (Accessed: 30/10/18).

McCluskey, A, Lalkhen, G, A. ‘Statistics III: Probability and statistical tests’. Continuing Education in Anaesthesia Critical Care & Pain. Volume 7, Issue 5. Available at: https://academic.oup.com/bjaed/article/7/5/167/534620. (Accessed: 30/10/18)

Victoria University (2017). ‘Basic definitions and concepts’. Available at: http://www.staff.vu.edu.au/mcaonline/units/probability/procon.html. (Accessed: 31/10/18)

Images

The Traveller’s Guide to the Best Manchester Land-Based Casinos

https://www.thoughtco.com/thmb/lvjed7xsmt0LaJWwoYxg-GadMNc=/768×0/filters:no_upscale():max_bytes(150000):strip_icc()/TwoDice-58bddad45f9b58af5c4aa0d4.jpg

http://math.ucr.edu/home/baez/games/games_9.html