Connectedness

Addition and Subtraction

(Liping Ma, 1999) quotes “Connectedness is where a teacher can show the children it is achievable to use one type of math they already know to solve another.” Addition and subtraction have an inverse relationship, and therefore is described in PUFM (Profound Understanding of Fundamental Mathematics) as ‘connectedness. For example, a number fact is made up of three numbers. These three numbers can also be used to make up other number facts. When the children know one, this helps them with others. Here is an example using the numbers 3, 4 and 7

Addition Facts                                                Subtraction Facts

3 + 4 = 7                                                             7 – 3 = 4

4 + 3 = 7                                                             7 – 4 = 3

Most children generally find subtraction sums harder to learn than they do with addition sums. However, if a child knows that 6 + 9 = 15, but the question is in fact 15 – 9, even though this question is a subtraction sum, they can find the answer out using addition. For instance, they can think 9 plus what are 15? And they are gaining the same answer, using a different method. (Math steps, no date) quotes “this use of thinking of the related addition fact when children encounter a subtraction fact they don’t know should be encouraged. Children often find themselves either counting up or counting back to solve subtraction and that is inefficient.” However, if children are aware of the important inverse relationship that addition and subtraction hold, this will make it easier for them to undertake subtraction sums. Therefore, as a teacher, it is important to reinforce this idea to the children. You can do this through questioning; using questions that encourage this strategy of the inverse relationship between addition and subtraction.

Multiplication and Division

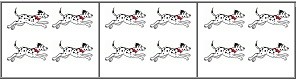
Multiplication and dividing also have an inverse relationship within mathematics. Multiplication and division are opposite operations and are both used in groups of equal size. (Lewis, 2005) quotes “Multiplication and division are very closely related. They are opposite operations. You could say division is ‘backwards’ multiplication”. Using this picture above, you can see that they can both be worked out using the same picture. For instance, if you have three pictures of four dogs, this can be written as 3 x 4 = 12 for multiplication and 12 ÷ 4 = 3 for division. Therefore, we can obtain both a multiplication fact and a division fact from the same picture.

Lewis, M. (2015) Understand multiplication and division relationships. Available at :http://learnzillion.com/lesson_plans/8460-understand-multiplication-and-division (Accessed 2 December 2015).

MathSteps: Grade 1: Inverse relationship between addition and subtraction: What is it? (no date) Available at: http://eduplace.com/math/mathsteps/1/b/index.html (Accessed: 2 December 2015).

Did you ever realise that your kitchen can be like an in-house classroom and a great space for learning? Well it can. In your kitchen, you can learn lots of different things other than just learning how to make a meal, like mathematics for instance. Even the simplest recipes require basic math skills. However, (How can math help you cook?, 2015) says expanding upon recipes can take you even deeper into fractions, multiplication, estimations, proportion and division!

Our kitchen is full of various tools that can link to mathematics in many ways. For example, (LZXpress, 2010) states that a measuring cup and jugs links to maths due to the use of measurement. If you were measuring solids and dry ingredients such as peanut butter, flour and caster sugar you would use a measuring cup. If you were measuring liquids such as water, you would use a measuring jug. Measuring jugs are split in to two sides, one side measuring cups and ounces, and the other measuring litres (l) and millilitres (ml).

For example, do you know the difference between a teaspoon and a tablespoon? They may not look that different, but (LZXpress, 2010) expresses when it comes to putting 3 tablespoons of salt in to your soup instead of 3 teaspoons, that is when it all goes wrong. I like to remember teaspoon as something you mix your cup of tea with, this helps me remember the difference. “A teaspoon is a common culinary measurement that’s equal to approximately one-sixth of a fluid ounce. A tablespoon is equal to three teaspoons.”

Moreover, if you are reading a recipe that is suitable for four people, but you want to make it for eight people, what do you do? Well four is double two, so you would double everything in the recipe. So for example, a cake recipe includes two eggs, you would use four eggs and so on. This way, the cake will be double the amount.

(How can math help you cook?, 2015) quotes “If a recipe calls for six teaspoons of vanilla extract and you want to double the recipe, how many teaspoons of vanilla extract would you need to include? If you only have a tablespoon, how many tablespoons of vanilla extract would you include? If you said twelve teaspoons and four tablespoons, you’re ready for the kitchen!”

How can math help you cook? (2015) Available at: http://wonderopolis.org/wonder/get-cooking/?replytocom=663004 (Accessed: 25 November 2015).

LZXpress (2010) Math in the kitchen. Available at: https://www.youtube.com/watch?v=wQkCBhQd7wM (Accessed: 1 December 2015).

I bet you did not realise that mathematics is all around us and used in everything we do. Yes, me neither, but it is true, mathematics is everywhere. Throughout the module ‘Discovering Mathematics’, this is the main thing that I have learned. Before starting this module, I had an idea of mathematics, but not to the extent I do now. For example, yes, mathematics is numbers. Numbers that you add together, you multiply and you subtract; all the things you get taught at school. However, never did I realise that mathematics was involved in sport, food, driving a car, cooking, singing, dancing, shopping; the list goes on and on.

Now that I know this, it seems obvious. Of course mathematics is involved in sport, for example, football. (Mahaney, 2011) helped me realise that football is played on a pitch that is measured in meters, it is a rectangle shape and it has two halves, the game involves two teams made up of eleven players each, and there is one referee. This list can also go on forever. Moreover, (Mahaney, 2011) expresses how the goalkeeper in football is 1 player out of 11 players in the team and 22 players on the pitch. What do we call this in mathematical language? Correct, ratio is the answer. Ratio can develop in football in many ways. One example is, if one player from ‘team A’ gets sent off from the referee, the ratio is 11:10 for team ‘B’.

For me, myself, being interested in football, I believe if my teacher at school explained ratio to me using football terms, I would have maybe understood ratio quicker. I may not have taken days, weeks and maybe even months to understand ratio fully before my final exam. In my opinion, when an individual is being taught a certain subject, they pay more attention if they are enjoying it, or they can relate to it. Therefore, this can help them learn this subject area quicker. (Liping, 2010) quotes “teachers must understand that elementary math consists of basic ideas. These basic ideas that recur through math learning create a solid foundation on which to build future math learning”. I would argue that if we started off with more basic mathematics, using simplistic examples on something we are interested in, we would be able to solve more in depth mathematic skills.

Liping (2010) Knowing and teaching elementary mathematics: Teachers’ understanding of fundamental mathematics in china and the United States. New York: Routledge.

Mahaney, I. F. (2011) The math of soccer. 1st edn. New York: PowerKidsPress.