Believe it or not, there are many mathematical concepts which permeate music. According to Rosenthal (2005) ‘Musical notations as octaves, chords, scales and keys can all be demystified and understood logically using simple mathematics’.
But how does music work? And where do maths and music meet?
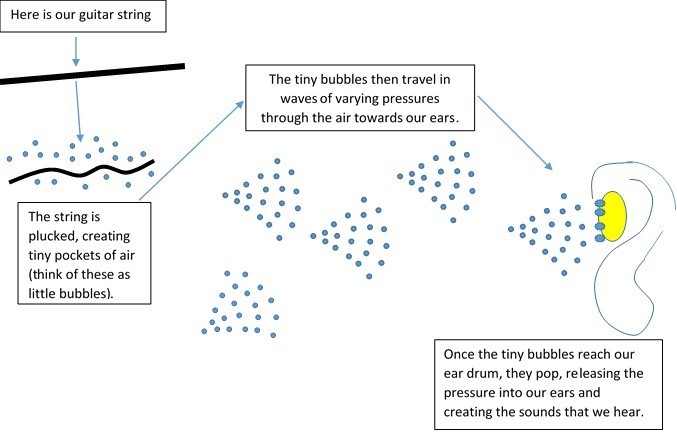
When a musical note is played for example, on a guitar, the string of the guitar vibrates. This gives off hundreds of tiny pressurised air pockets which travel through the atmosphere in waves of sound towards our ears. The air pockets then hit our ear drums, and create the musical sounds that we hear (Rosenthal, 2005).
Confused? Imagine this:
(Rosenthal, 2005)
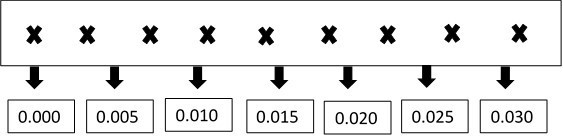
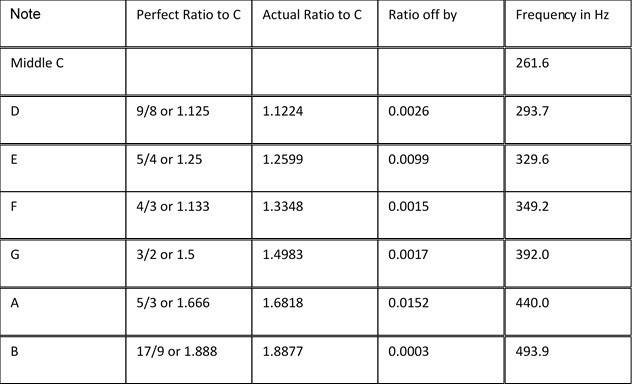
If we put this into an example as highlighted by Rosenthal (2005), using the notes Middle C and Middle G just, we can further depict the mathematics involved. The blue note in this example is Middle C, and the yellow is G.
According to Rosenthal (2005) the C note ‘has a frequency of about 262 Hertz. That means that when Middle C is played, 262 pockets of higher air pressure pound against your ear each second’ (Rosenthal, 2005).
If we place this into a basic graph, it would look like this:
Seconds
(Rosenthal, 2005)
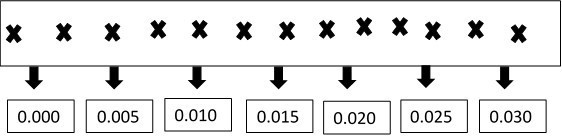
It is through using these graphs that we can depict the relationship between musical notes. If we take the frequency graph for note G and compare it to note C, we can see that the air pockets move at a faster pace for note G. This is because it holds a higher frequency of 392Hertz (Hz), creating a higher pitched note:
Seconds
(Rosenthal, 2005)
Rosenthal (2005) states that ‘by using knowledge of sound frequencies carefully, such musical mysteries as octaves and chords can be unravelled’ and this is where our mathematical adventure of music will take us next.
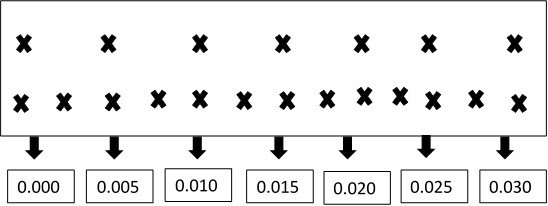
Using what we know about air pockets and frequencies, we are able to explain why certain notes sound good together and why certain notes do not. If we plot the notes C and G together on a frequency graph, it can be seen that the notes meet at regular intervals:
Seconds
(Rosenthal, 2005).
Translated into a waves graph it looks like this: (Middle C: Orange) (G: Blue): 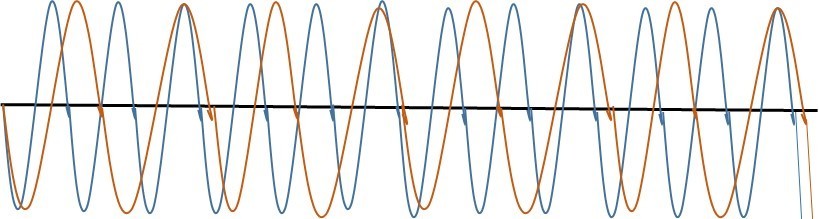
This graph shows the waves to meet on every 3rd G note and second C note soundwave. This equates to the ratio of 3/2, and this is what creates a sound that is pleasing to our ears. This is the case as the difference between the middle C note and the G note is only off by ‘0.0017’ seconds, creating a pleasing rhythm of air pockets which hit off of our ear drums (Heimiller, 2002).
This can be shown through an example taken from Heimiller (2002):
The ratios can be worked out using the information from the sound wave graphs. For example:
‘9/8’ can be equated into the sum: 9 divided by 8 = ‘1.125’.
(Heimiller, 2002)
This however, is an imperfect ratio as the numbers have been rounded (Heimiller, 2002). Although the reason why is not described, I beleive that a possible explanation could be as a result of the untraceable changes within the frequencies to the human ears as the air pockets are so tiny.
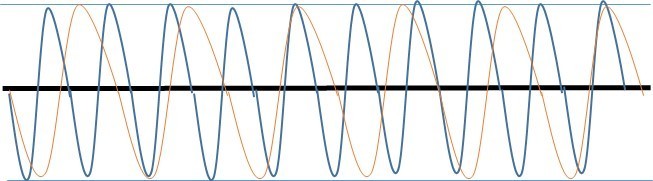
The further out the ratio from middle C, the more displeasing the rhythm of air pockets, creating what our ears hear as displeasing sounds. This can be represented through a sound wave graph which depicts the frequencies of the notes Middle C and A- the two notes with the highest difference in frequencies (Heimiller, 2002):
The notes repeat frequencies at less common intervals, creating a barrage of tiny air pockets which hit the ear in an unpleasing rhythm, this creates unpleasing sounds to our ears.
Links to fundamental mathematics and a wider world context:
Despite the topic of maths and music being quite confusing at times, the maths boils down to the basic principle of patterns. The smaller the difference in ratio of the air pockets, the more frequently the sound waves meet. This creates more repetition of frequencies within the notes, creating a sound which to our ears is similar, or which blends well together, for example in chords. The patterns created by the air waves, allows for similar notes to be put together. This can often be translated into patterns within musical pieces, as composers are more likely to put notes and phrases of music together within a piece if they sound pleasing together. This knowledge of music and musical notes has contributed greatly over the years to the way in which music is created. On a whole, composers will attempt to make music which at some point has repetition of either notes or phrases as it is pleasing to the ear, and could be said to be more likeable to listeners than music which follows no repetition.
Relation to Practice:
The basic principles of the maths behind music can also be related into teaching practice. I believe that this is possible through children’s engagement with different rhythms and beats within music. When learning about music, often one of the first things that children will look at is being able to follow a simple beat. This can be taken from basic repetition of the teacher clapping her hands to looking at beats and rests in music. This on a very basic form allows children to understand the process of patterns. This can be built up throughout music to look at timings in music, which are able to be broken down into fractions.
References:
Heimiller, J (2002) Where Maths Meets Music. Available at: https://musicmasterworks.com/WhereMathMeetsMusic.html (Accessed 19th November 2015).
Rosenthal, J (2005) The Magical Mathematics of Music. Available at: https://plus.maths.org/content/magical-mathematics-music (Accessed 19th November 2015)