During the Maths in Sport workshop, we looked at the factors that make up a football league table. Our task was to redesign the league table from 1888/89 to match a modern day premier league table. Both tables featured the results from the 132 matches played, the wins, draws, losses, goals for, goals against and total points for each of the 12 teams. However, the modern table had the goal difference and the total number of matches played by each team. The goal difference was calculated by subtracting the goals against from the goals for. We could have also calculated up the average number of goals per game by dividing the total number of goals by the number of matches played. The points were calculated using the following equation:
Points = (No. of wins x 2) + no. of draws
Below is the original table, a modern day premier league table and our modern version of the 1888/89 table:
Maths is clearly required in football whether that be for league tables, the size of the pitch or the weight of the ball. As explored before, it is used in other sports such as field hockey. Another sport we looked at was sprinting at the Olympics. It is pretty obvious why maths is needed here- for the times and distances in a race. However, an interesting point was made when we were shown a video (Wimp, 2012) on the history of 100m sprint winners and how runners have got faster as time has went on. One way maths could be used here is to compare the different times for runners and considering the average time and the average age of the winners or the average distance travelled per second.
In groups, we then went onto creating our own sport or further developing a sport which already exists, considering the mathematics involved in it. My group decided to create our own sport- Smack-Ball. The idea of the game was that there would be 2 teams, each with 3 players and the goal was to using only your hands smack the ball off the opposite wall from where your team started. By alternating the hand the ball is on and then passing to team mates, it would then be possible to smack the ball off the wall. However, the opposing team are able to intercept and whack the ball out of your hands. At this point, the first team to pick up the ball has possession. The ball would be hand-span sized to make it a manageable size and 196g (two thirds the weight of a volleyball). The court would be 10m by 5m to make it possible to pass to just one player who could then smack the ball off the wall if they applied a great enough force. Each game would last 10 minutes as only 6 people would play at once so may get tired more easily.
We thought that we could use maths in our sport in the following ways:
- Using the Pythagoras’ Theorem- This allows for the perfect pass to be made if each team member is positioned correctly. Whilst this would obviously be very difficult in the game, it could be the starting formation after a point is scored. Teams could also discuss their positioning after a game if it was recorded to determine tactics to improve their performance;
- To determine the force and distance required to hit the ball off the wall to score a point;
- To determine the perfect time to intercept a pass or the ball out of your opponent’s hand;
- Ball speed and spin.
After discussing our idea with Richard, we actually discovered that we had created a game which was similar to a popular craze in Ancient Mayan society. Here is a video explaining the game:
Without a doubt, maths is required in many sports to achieve optimum performance. I believe that this could be an interesting lesson idea as children could develop upon a sport they play or are interested in or they could enjoy using their creative side to create an entirely new sport. They could consider the links themselves and then share with other groups who could contribute, allowing children to build upon each other’s ideas. A whole class discussion could then be had on the principles of maths applied in several sports. It could also link into a PE lesson where they look at the idea of maths in sport e.g. time to run 100m, repeat a few times and then average their time.
Museum Secrets by Kensington Communications (2012). Rubber Balls in Mexico: A Long History and a Mayan Tradition. Available at: https://www.youtube.com/watch?v=_ZYpRsxqfFg (Accessed: 8 November 2017).
Wimp. (2012). Usain Bolt vs. 116 years of Olympic sprinters. [Online Video]. 5 August 2012. Available at: https://www.wimp.com/usain-bolt-vs-116-years-of-olympic-sprinters/?dm_i=LQE,25SE0,3LDIRH,7T51A,1/ (Accessed: 8 November 2017).
Field hockey teams usually consist of 16 players, 11 on the field and 5 reserves.
When trapping a hockey ball, a player’s stick must be at a 120 degree obtuse angle when first moving the stick in a motion to meet the ground. This specific angle helps the player have more control over the ball when first stopping it; it also gives the players more time and skill to continue playing.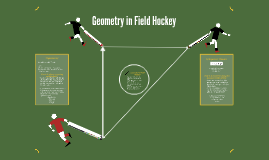
Pythagoras’ Theorem relates to field hockey through the triangle passing in the sense that three hockey players can successfully eliminate their opponent through correct distance measurements.
A clock’s structure relates to a hockey player’s tackling structure in the sense that a player is able to successfully tackle their opponent through the following:
As with most sports, time is crucial. It is needed to ensure that the game lasts for the set time. A collegiate field hockey game is divided into two halves each lasting 35 minutes in length. Half time lasts seven minutes. At half time, the teams switch playing sides. If a game is tied at the end of regulation, there will be two seven-minute periods of play.