As week 2 has drawn to a close, it is hard to believe that the Easter holidays are already upon us. The past two weeks have flown by but I am ready for a little break before facing the four week block.
This past week has allowed me to experience teaching when there are various things happening within the school community. With Friday being a half day, there was little time for direct teaching. There was a morning assembly which I really enjoyed as it was all about the Easter story and we sang two songs. As I am a Christian, I found this a nice experience of reliving my childhood especially compared to my experience of a Roman Catholic mass last year on Ash Wednesday. As terms come to an end, it is important to tie up any unfinished work and tasks. This may include tidying the classroom, finishing crafts and ensuring that as the teacher you have everything you need over the holidays. School is not just about educating pupils academically but also for life, children need to learn to tidy up after themselves and take responsibility.
Often, with the end of term comes a lower attention span and some children may act up, we found it was harder to keep children focused on a task and more fun activities were introduced. I believe it is essential that school is a place of fun and Easter provides the perfect opportunity for craft and Easter egg hunts! I led a craft with the children in groups of 3 or 4 which allowed me to get to know the pupils better. We made Easter chicks over the course of the week which the children responded well to. I learned of the importance of ensuring all materials are ready before the children begin. At times, I think I wasn’t firm enough with the pupils and let them away with too much talking and not enough sticking! Next time, I need to ensure children listen to exactly what they need to do and know to use indoor voices and keep talking to a minimum. Additionally, the children had a time of play, something which is a key focus in the NI curriculum. During this time, it is important that the teacher does not just sit back at their desk, we need to get involved and show an interest in what children enjoy playing with. Even better, we get to play too!
I spent Wednesday and Thursday at the Primary 7 boys and girls’ inter-schools hockey tournaments. This gave me valuable experience in taking children outside of school and the logistics involved e.g. booking a bus, ensuring all pupils have what they need and are safe. It is important to have good relationships with other schools particularly at these tournaments. I believe that whilst we can be competitive, we need to be friendly towards our competition and support other schools if we do not make it. I enjoyed chatting with other staff to discuss their teaching experiences as no teacher has the same experience. Interestingly, all of the teachers I spoke to had studied in Northern Ireland, some with a Bachelor of Education, some with a PGCE and one with a PGDE. Hearing the experiences of others helps me feel that studying at Dundee was the right decision for me. Whilst studying at home would have been A LOT cheaper, I think studying the MA (Hons) Education course at Dundee will be worthwhile. It brings me a little comfort when I hear of teachers who questioned if they really wanted to teach during their uni days. I am constantly reminded that placement is not the same as having your own class. It was nice to work with older pupils for a couple of days and act more as a coach rather than a teacher. I was able to reminisce on my hockey days at primary school especially our dramatic final which ended in us losing by 1 goal in sudden death of penalty flicks. I think my anger at losing by just one point came out as my determination for the girls and boys to do well!
Thankfully, I managed to get some teaching fitted into this busy week! The usual Monday morning routine circle time proved rather successful on the theme of ‘Friends Letting Us Down’ to link to the Easter story when Judas betrays Jesus. I took a risk through introducing a new and quite complicated game which focused on lying. This risk proved worthwhile as the children seemed to really enjoy it and it got the message across. The children who were lied to during the game could express how they felt and compare that to how Jesus may have felt. This led well into a discussion on what we should and shouldn’t do to be a good friend. I felt that the class were quite chatty at times but managed to bring them back anytime they seemed to be losing focus. I had to speak to a couple of children on multiple occasions and stupidly didn’t think to make them sit out as they were not considering their actions and changing their behaviour.
On Tuesday, I taught the children about CVC words with ‘og’ and ‘od’. I was not happy with this lesson for various reasons. I thought I had from 9.20-10.20 to take the lesson, however, at 9.45 I was informed by Primary 7’s that there would be an early break at 10am due to the Easter lunch. At this point, I had only finished the introduction, explanation and discussion with the children, meaning they only had 10 minutes to get their workbooks and table trays and get their work done. This was not enough time at all! To add to this surprise, I thought the workbooks were on the teacher’s desk, however, only a couple were! Next time, I must ensure that everything I need for the lesson is sitting ready. Thankfully, the class teacher returned to the classroom a few minutes after my wild goose chase for the workbooks and the children could begin their work for all of 5 minutes! This was a reminder that we need to be prepared for the unexpected and to alter our plans.
Several of my class attend ‘Cabin Club’ after school each day. This is for children who finish school at 2pm and cannot be collected until 3pm, perhaps due to older siblings in the school who only finish at 3pm. This takes place in the mobile classroom which is a play based learning classroom with an outdoor area including a shed, kitchen area and various outdoor equipment. It is not a homework club but instead a space for children to explore through play. I helped out with Cabin Club on Wednesday afternoon. As the weather was nice, the children played outside. I think this is a great idea as it allows children to get some fresh air and exercise after a day at school whilst also providing them with learning opportunities, often, without them even realising they are learning showing that learning can indeed be fun!
Whilst this week has been busy, I have enjoyed it and it has allowed me to see that sometimes things do not run as smoothly as we like and timetables are interrupted. As a teacher, I need to be prepared to change the plan for the day when something else crops up. It is good as a student to get out of the classroom and get involved with sports outings without the pressure of organising it. This prepares me for the future if I ever end up as the coach for a sport. It has been a speedy but hectic week with nose bleeds, sick children and tired teachers but hey I guess that’s the life of a teacher!
Before clocks existed, many people relied on nature to grasp the concept of the passing of time. For example, the movement of the sun across the sky would indicate day and night. It is believed that in the past, ancient people divided the sun’s cycle into different timekeeping periods. For example, the ancient Egyptians built tall obelisks that would cast shadows to help divide the day into sections (Wonderopolis, 2017). We watched an interesting video on an elephant water clock in class (Luppino, 2015). I was fascinated by the mechanics and level of maths behind this to make everything work at the right time.
Whenever I was younger, I used to think that the whole world was at the same time of day as me. Obviously, I later discovered this was incorrect. The idea of time zones is just amazing and very relevant for me. I have several family members in Canada including my brother and friends in places such as New Zealand. It is therefore necessary for us to consider each other’s time differences before we Facetime. This is especially strange with Kiwis as they are 13 hours ahead which means they are often a day ahead in a sense.
Maths is crucial in timetabling as you need to schedule different lectures for different times and ensure that no room or lecturer is double booked. This is a complex process and something I don’t think I could do! The idea of sitting with pages of names, subjects, rooms and lecturers to sort into a timetable just freaks me out! Would it be easier to use computer timetabling to get an automatic timetable for all students and lecturers? Whilst it would probably be a lot easier and quicker, there would be a lack of personal touch in that nobody wants a 4-5pm lecture on a Friday! Furthermore, a lecture could finish at 11am in the Tower Building and the next one start at 11am in Dalhousie. There is no way you could make it to lectures on time if this was the case.
Whilst at school, I studied A level Applied ICT. This involved creating a game, another aspect of computing that requires maths. The idea of direction was crucial in my game as it was a maze game. The number of coins that were collected needed to be calculated up and the character needed to only be able to move within the game path. I also used the programme Scratch where I created Sprites. This involved programming the sprite to move X steps in a particular direction and turn different angles. This is something I would definitely consider using in the classroom to allow children to see basic maths in action within gaming.
We started off the lecture by considering a restaurant which had 2 choices of starter, 3 choices of main and 2 choices for dessert and how many different combinations the restaurant could serve. I worked this out by giving names to each dish e.g. Tomato soup, steak and chips and chocolate fudge cake. I then wrote out each starter and completed the meal by changing the main and dessert each time. I concluded that there could be 12 different combinations. This would be a good starter activity in the classroom to get children thinking about the probability of getting a certain selection of dishes.
In the counter intuitive maths lecture, we considered this idea with socks- 4 black, 4 red and 4 blue and how many socks you would need to make a pair. The answer is 4 as you only need 1 more sock than the number of different colours. Again, this is something which could be explored in the classroom.
A die is one of the most commonly used objects within probability and is used a lot in gambling. It is unlikely I will use gambling as a main tool to teach probability, however, I will use the idea of rolling a die. Some activities could include getting children to record what they roll for a certain number of throws or asking them to calculate the probability of rolling certain numbers e.g. the chance of rolling a 5 on a 6-sided die i.e. 1/6. They could then look at throwing a 5 on both 6-sided dice i.e. 1/36. The probability of this happening is actually calculated by subtracting the probability of it not happening away from 1. I have explained this below:
Before this input, I would not have known that this can be used in gambling and slot machines to work out the chance of winning or losing. Maths is used when designing the likes of slot machines as the probability of an outcome multiplied by the pay-out/prize for that combination will never equal to 100%. This means that slot machines will always win and earn a profit, never the player. Additionally, this can be ‘weighted’ so that bigger prizes or frequent smaller prizes are paid out, resulting in more money for the casino (Holme, 2017).
There is more to gambling than just luck, there is fundamental mathematics behind it. For me, I don’t think that gambling is worth the time or the money unless you are crazy and rich enough to do as Mandel did. However, a lot of countries have now banned this technique so it’s probably not worth your while really! I think I will keep to the likes of rolling dice and flipping coins to explain chance and probability in my classroom!
As someone who does not consider themselves musical, I hadn’t really put much thought into how maths is needed in music. I love listening to music and find it a great way to relieve stress whilst belting out a song! However, I studied music in school and absolutely hated it. I would dread walking into that classroom to be asked to play the Eastenders theme tune yet again on the recorder or be asked yet another music related question that I had no clue how to answer and to be frank didn’t care about! I knew of the basic elements of music e.g. tempo, rhythm, dynamics but I didn’t fully understand how maths held such a great purpose in music. After our input with Paola, my eyes have been opened!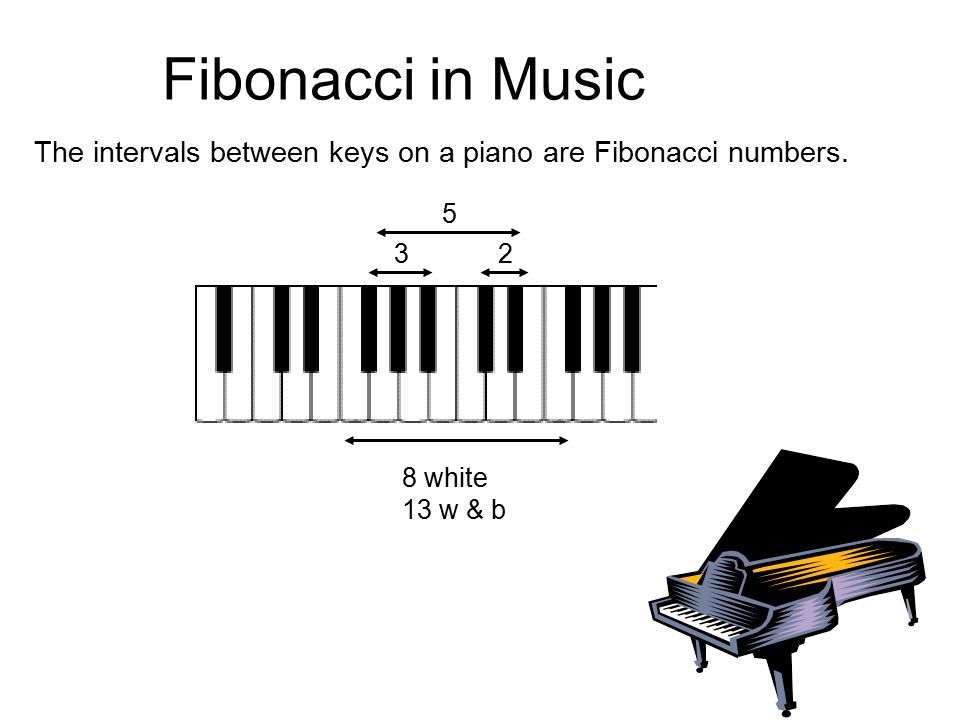
In pairs, we had to think of as many links between maths and music as possible. Megan and I came up with quite a few including the note values, beats in a bar, the actual making of an instrument and counting songs. Other ways in which maths and music link include tuning instruments, figured bass, scales and even the Fibonacci sequence! This is because there are 13 notes in an octave e.g. from C to C. A scale is composed of 8 notes. The 5
Many people scrunch up their face or roll their eyes when they think of maths, many believe that it is boring. I reckon it does not have to be that way- maths can be fun! I believe that we as teachers need to liven up the idea of maths and bring in cross curricular learning as well as looking at learning mathematics through play.
Research has shown that previous traditional teaching methods have not been successful as when adults were asked to explain how to solve particular problems and why we need certain mathematical concepts, they were unable to recount their learning. These rote and drill teaching methods such as handing pupils a page of calculations to complete has been referred to as shallow learning as it did not make complete sense to pupils. Parents and teachers are now worried that the maths that parents pass onto their children is not solid and accurate yet it is crucial that parents play an active part in the mathematical learning of their children particularly during the early years (Valentine, 2017). It is important for maths to be a continuous part of the home environment through aspects such as time (for cooking), money (bills) and telling the time to help encourage the learning.
Play is important because it is a major part of children’s everyday world- for them it is a familiar environment, resulting in more successful learning as it is a meaningful context. Furthermore, play helps them to develop social skills such as sharing e.g. they can use maths in a role play situation e.g. play shop. Play also allows children to learn in their own time and be independent learners. They are able to control what happens during their learning and the outcomes of it. By using play to learn maths, children are able to visualise their learning instead of using a textbook e.g. use of 3D shapes. Play allows children to experiment in a relaxed environment where making mistakes is not an issue and written outcomes are not a focus.
There are many forms of play which can be used for learning. These include symbolic, creative, discovery, physical, technology, games, environmental and books and language. Activities may include rhymes, outdoor play, songs and role play. We looked at a video on maths in literature where mathematical concepts were used in traditional fairytales and stories such as Goldilocks and the Three Bears which changed to Goldilocks and the Three Squares. Something as simple as this is a great way to introduce children to basic concepts in maths.
Tessellations of congruent shapes, such as above, are called monohedral tessellations. The word monohedral literally means ‘one’ – mono and ‘shape’ – hedral. Regular tessellations are made up of only one regular shape repeated, whilst semi-regular tessellations are made up of two or more regular shapes tiled to create a repeating pattern. A lot of Islamic art uses tessellations of equilateral triangles, squares and hexagons. Furthermore, in Spain there are many examples of art in tiling such Park Güell in Barcelona.
Snowflakes are another example of maths in nature. They exhibit six-fold radial symmetry, with elaborate, identical patterns on each arm. Snowflakes are made entirely of water molecules which have solidified and crystallised to form weak hydrogen bonds with other water molecules. The bonds maximise attractive forces and reduce repulsive forces, allowing the snowflake to form its hexagonal shape 
Maths is even required in photography. Many photographers use the ‘Rule of Thirds’ to set up their photos. This is where the image in broken down into 9 sections using 4 lines. The idea is that if you capture an image where the main object/focus is placed along the lines or the intersections, the photo will be more natural and pleasing to the viewer instead at the centre of the shot (Rowse, no date). Another method photographers use is balancing elements. This is similar to the rule of thirds and is simply placing a focal point off centre to create a more interesting image, however, this means there is empty space at the opposite side. This is where balancing elements comes in- you place another similar object at the other side to balance the photo out- known as formal balance. Informal balance is when you place two varying objects at opposite sides of the image (Google, no date). Leading lines are another method used in photography in which straight objects such as roads are used to draw the viewer’s eye to the image and connect the foreground to the background (McKinnell, no date). The final method photographers use is symmetry and patterns within photos to create a balanced and aesthetically pleasing image (DMM, no date).