As preparation for our Maths in Sport input, we were asked to consider the mathematics used in a certain sport. I chose field hockey as I played it for several years when I was younger. I had never really considered that maths would have a part to play in field hockey and simply just thought about playing rather than the maths behind it. What I found in an online article by Tohi (2016) surprised me!

Field hockey teams usually consist of 16 players, 11 on the field and 5 reserves.

On the field, there are usually:

• 3 strikers: left wing, centre forward and right wing
• 3 mid-fielders: left half, centre half and right half
• 5 defenders: left full back, sweeper, centre back, goal keeper and right full back

Design of Field, Ball and Stick

A hockey field forms the shape of a rectangle, the length being 91.4m (100 yards) and width being 54.8m (60 yards). The design on a hockey field holds the following geometrical figures- 10 parallel sets, 16 right angles and 2 semi-circles. The hockey field is also divided into 4 sections; these four sections form smaller rectangles that are about 22.8-22.9m long. The line segments that separate the field are all parallel to each other and perpendicular to the point where they meet the side of the field.

The ball used to play hockey is a perfect sphere, so when passed it will go in the direction it was hit. The hockey stick, when it comes into contact with the ball is tangent to the circle at the point where it meets. The more force that you use to hit the ball, the farther it will go, so by determining the velocity of your hit you can decipher the distance the ball will travel.

It is also important to consider the weight of the stick and ball to ensure that the ball is not too light that a slight tap will send it way down the pitch but not so heavy that it requires a great force to move the ball. The stick should be quite light to allow players to use it with ease.

Positioning

When trapping a hockey ball, a player’s stick must be at a 120 degree obtuse angle when first moving the stick in a motion to meet the ground. This specific angle helps the player have more control over the ball when first stopping it; it also gives the players more time and skill to continue playing.

When hitting the ball, a player must position their body at a correct angle. If the knees aren’t bent enough and the angle is too large, the stick won’t reach the ball, however, if the player’s knees are bent too much, and the angle is too small- the player will more than likely take a chunk out of the field (if grass) or hit the field instead of the ball (if astro).

In addition to this, if a player swings their stick and the follow through has an angle measure greater than 90 degrees, the player will get called, making the other team now have possession of the ball.

Pythagoras’ Theorem in Triangle Passing

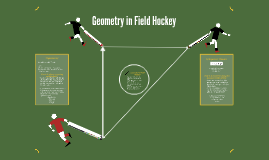Pythagoras’ Theorem relates to field hockey through the triangle passing in the sense that three hockey players can successfully eliminate their opponent through correct distance measurements.

For example, if player A is 7m from player B, and player B is 5m from player C, how far should player C be from player A in order to successfully perform a triangle pass?

c²=b²+a²

c²=7² + 5²

c²=49 + 25

c²=74

c=√74

c=8.6m

Clockwork Structure

A clock’s structure relates to a hockey player’s tackling structure in the sense that a player is able to successfully tackle their opponent through the following:

• 2 o’clock
• 3 o’clock
• 9 o’clock
• 10 o’clock

However, in this sense, the stick must be positioned at an acute 80 degree angle in order to keep the ball connected to the ground with force and strength behind the hockey stick.

A player’s feet must be parallel or facing in outward 30 degree angles in order to maximise extra force and knees bent at a 120 degree angle.

From this type of geometry and maths behind positioning, a player is able to attain success in tackling.

Time

As with most sports, time is crucial. It is needed to ensure that the game lasts for the set time. A collegiate field hockey game is divided into two halves each lasting 35 minutes in length. Half time lasts seven minutes. At half time, the teams switch playing sides. If a game is tied at the end of regulation, there will be two seven-minute periods of play.

 

It is evident that mathematics appears a lot in field hockey and there are likely more ways in which it features that I am not yet aware of. This is the same for many sports and I believe that it is important that we begin to explore these aspects with children. It not only relates maths to their world but also may be a topic of interest for many children helping to inspire them and show them that maths is not just within the classroom.

 

Tohi, K. (2016) Maths in Field Hockey. Available at: https://prezi.com/3mk2gu_u74ph/maths-in-field-hockey/ (Accessed: 8 November 2017).