In one of our inputs with Richard, we looked at exploring mathematics within sport. I was not surprised that maths was an integral part of sport, unlike art and stories, which was more surprising to me.
We were given the first ever recorded football league table to look at.

Here is the English league table from 1888.
Our first task was to take this league table and convert it into a league table that is used today. What we first noticed was that the old league table was ordered alphabetically, whereas league tables today are ordered by points. We looked at the table and figured out that Preston football club would be at the top based on points. We continued ordering the table in this way until we got to Bolton Wanderers and West Bromwich, as they both had the same points. When this happens, the teams are then ordered by the best goal difference. This also happened with the last two teams, Notts County and Stoke. We placed Stoke 11th and Notts County 12th, however, we noticed that on the old table, it was the other way round.
The reasoning behind this was because goal difference was not counted in league tables until 1970’s. Instead, if two teams had the same points, they were ordered by the amount of goals they had scored. In this case, Notts County had scored 39 goals compared to Stokes 26 goals, putting them higher up in the table.
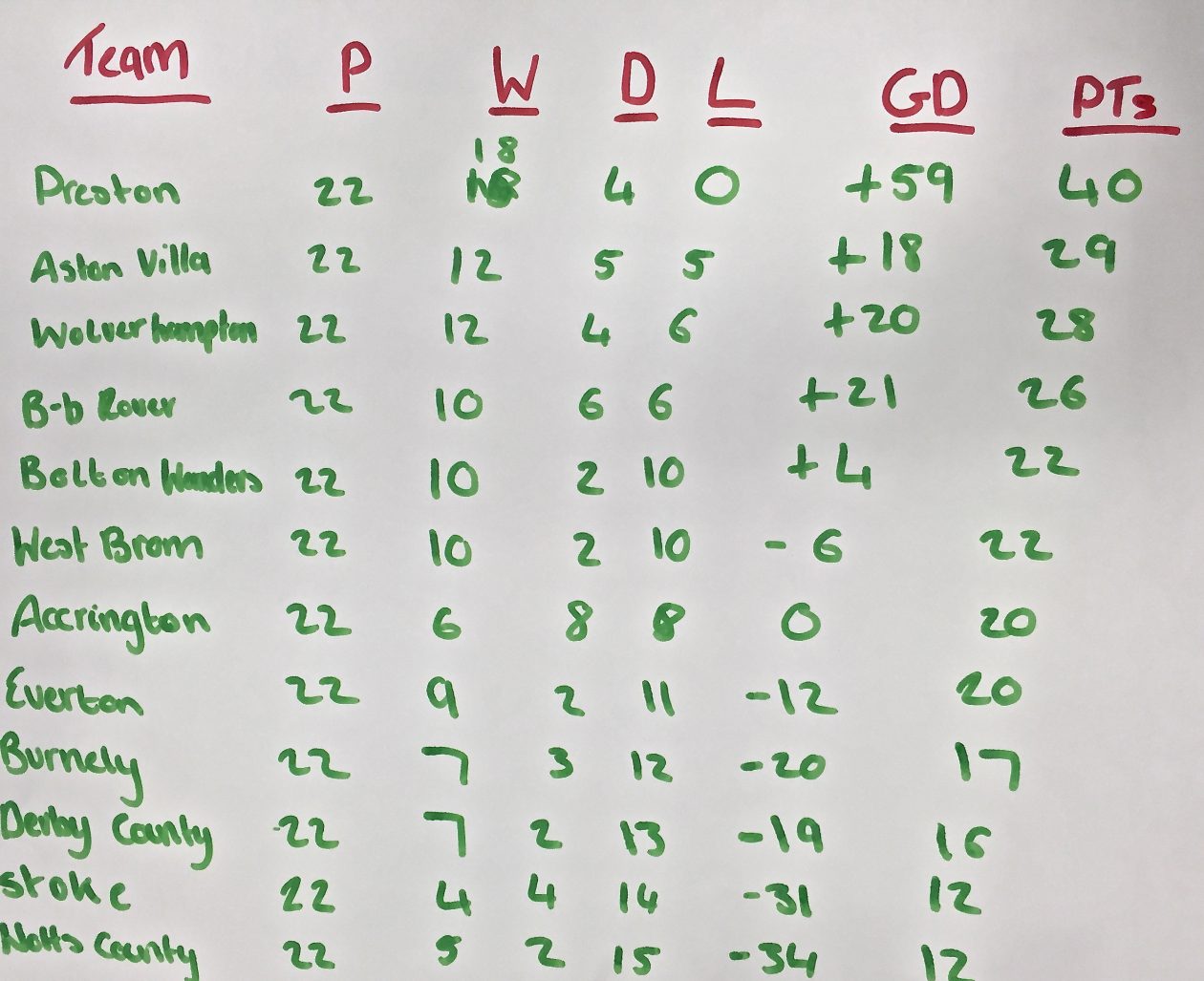
Here is the league table we made based on modern day tables.
The next task we were given was to take our own knowledge of a sport and look at the mathematical perspectives behind it. Our group chose Taekwondo, as Amy participates in this sport and has a great knowledge of its rules and formats.

Here is the mind map that we came up with, showing the different mathematical perspectives and rules.
The rules of Taekwondo are as follows:
- Punch = 1 point, kick to body = 2 points, kick to head = 3 points
- 1 vs 1
- Points lost for illegal activity
- Divisions are based on weight
We then had to change the rules to see how it could potentially change the game.

This is the rule changes we decided to come up with.
The first aspect that we decided to change was the ring size; after each round ended, the ring size shrunk for the next round. We decided on this as some competitors may use the ring size to their advantage, by avoiding the opposition, and with a smaller ring size, they couldn’t do that. We also decided to shorten round time for this same reason. Another aspect that we changed were the divisions. Previously, the divisions were split by weight, which was changed to height. This was because if two competitors in the same weight divisions had a big height difference, it would be hard for the smaller player to achieve a kick to a head to gain maximum points. The next rule that we changed was the points. Instead we decided on: punch to body – 1 point; punch to head – 2 points; kick to body – 3 points; kick to head – 4 points. We decided to make our final rule change a bit quirky – changing the players from 1 vs 1 to doubles which we liked to name ‘two-kwondo’. We thought of it as similar to the idea of tag teams in wrestling.
As a result of this input, I feel that my knowledge of maths in sports, especially taekwondo has improved. Looking at this has also made me realise how changing the rules of a sport can dramatically change the outcome of the game. I will keep this input in mind as a lesson for when I am teaching, as this would be a really fun activity that the pupils would really enjoy as they can really get involved in it. It will allow them to see beyond the basic rules of sport, and view the mathematical concept behind it.
References
Wright, C. (2016) On this day in 1888: Preston the big winners as first football league results recorded. [Online] Available at: http://www.whoateallthepies.tv/retro/243184/on-this-day-in-1888-preston-the-big-winners-as-first-ever-football-league-results-recorded.html [Accessed 22nd November 2017]


I really enjoyed doing this activity with you in our group and the blog response was very interesting to read! I think that it was really important for us to see the different variables that go into sports, and how mathematical they really are.