Growing up maths and music were two of my most favourite subjects so I thought it was only right that I did a blog post about the links between them and the maths rooted in music. Having played the keyboard and piano since I was 8, I have a deep understanding of all things music, from the fractions involved in musical notes to counting semi-tones to find a chord. However, there is more maths in music than I ever realised which is a great discovery in terms of making maths enjoyable for learners and using different routes to teach it, for example through maths.
Firstly, in this weeks maths input I learnt about patterns in relation to music and maths which I found of particular interest after one of my previous blog posts on Islamic Tilings. Through my research, I discovered that music is an example of a hierarchical system as patterns are nested with larger patterns just like characters form words which form sentences, chapters and eventually a novel. Composers have been exploiting this concept of hierarchies for thousands of years, maybe even unconsciously, but surprisingly it’s only recently that these systems have been understood mathematically. This type of maths shows us that principles of musical composition are shared among diverse hierarchical systems (a form of patterns) which suggest there is still may more exciting avenues to explore.
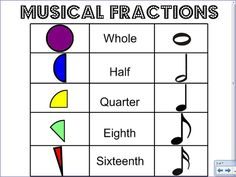
Whole numbers and fractions are everywhere when it comes to music and are especially important as it enables musicians to read music and interpret the length of a beat easily. This is crucial when playing in an orchestra as everyone needs to stay in time with each other. So to give a bit of background for all the non-musicians out there, each note has a different shape which indicates its beat, length or time. Additionally, notes can be classified in terms of numbers. Whole notes consist of one note per measure, half notes – two notes per measure, quarter notes – four notes per measure, eighth notes – eight notes per measure and sixteenth notes – sixteen notes per measure. These particular numbers are used to signify how long the notes will last. For example, a whole note would last an entire measure whereas a quarter note would only last a quarter of a measure, therefore, there is time for four quarter notes in one measure. Which is expressed mathematical as 4 x 1/4 = 1. Furthermore, there is a dotted note which involves placing a dot after a note lengthening it by a half of that note. For example, a quarter note with a half would be held for 3/8 of a measure, expressed mathematical as:![]() In conclusion, it is essential for musicians to understand the relationships and values of fractions in order to hold the note correctly, therefore, linking maths and music!
In conclusion, it is essential for musicians to understand the relationships and values of fractions in order to hold the note correctly, therefore, linking maths and music!
Finally we come to Fibonacci as believe it or not, it also links to music (and patterns!). As I’m sure you know, the Fibonacci sequence is a famous and well-known sequence that follows as: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89… and so on, where it uses the pattern of adding each term to the one before it to create the next term. For example, 5 + 8 = 13, 8 + 13 = 21, 13 + 21 = 34 and continuing to infinity. In music the Fibonacci can be seen in piano scales which is something I used to dread as a child (they’re no fun to learn). For example, the C scale consists of 13 keys from C to C (eight white keys and five black keys, with the black being arranged in groups of three and two. Additionally, the ratio between each term is very close to 0.618, which is known as the golden ratio.
I could continue on for pages about all the links that are present among maths and music. I find it particularly interesting as I had no clue just how many links can be made. In relation to Liping Ma’s 4 interrelated properties this particular post refers to longitudinal coherence as achieving a fundamental understanding of the whole curriculum you are prepared as a teacher to use any opportunity that may present during learning to review any critical concept where needed. For example, when teaching a music lesson if the opportunity where to arise, you could go over a mathematical concept to reinforce students previous learning. For future reference, what I have learnt through writing this blog post and my research will be taken into account when teaching as I think it will be of great benefit to the children to learn maths through music as for many it is their favourite subject whereas maths can be considered boring or difficult.
References
Buehler, M.J. (2014) The universal patterns of nature. Available at: http://www.slate.com/articles/health_and_science/new_scientist/2014/02/patterns_in_music_and_the_natural_world_creating_stronger_spider_silk_and.html (Accessed: 4 November 2016)
Glydon, N. (no date) Music, math, and patterns. Available at: http://mathcentral.uregina.ca/beyond/articles/Music/music1.html (Accessed: 4 November 2016).



I think the idea of linking music to maths in school is a great one. Even the idea of organizing sequences of sounds and creating and patterns to provide a pleasing composition is mathematical. So music is mathematical. Or is it that maths is musical? Now I am not sure myself!?