Category Archives: 3.4 Prof. Reflection & Commitment

Maths games, puzzles and fun

In a recent discovering mathematics workshop, we explored the mathematics behind various different games and puzzles. Board games are always something I loved as a young child. I would spend many days with friends and family surrounding a board game and having fun.

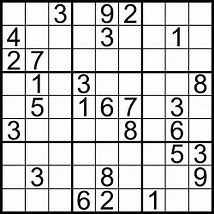
In this workshop we began looking at Sudoku. A standard game consists of a 9 x 9 grid with 81 cells however this can vary for more advanced and difficult Sudoku players. The aim of the game is to have the numbers 1-9 in a row, column and in a square. Normally when you start there will be some numbers that are already filled in and then you have to try and explore the different numbers that could fit. This is a game I have spent many plane rides or long car journeys playing however I have never really thought about the mathematical concepts behind this game. Some of the basic mathematical concepts in Sudoku is number, sequencing and problem solving. Throughout the workshop I learned that there are many different mathematical ways that people use in order to complete a Sudoku challenge. Upon further research I also found out that there 6670903752021072936960 different solutions to a standard 9 x 9 Sudoku grid (Felgenhauer & Jarvis, 2005).

Do you think you can complete a Sudoku? Give it a go!

We then went into groups to investigate different games and decide what mathematical processes were involved. My group decided to look into the game of battleships. In this game you place your ships of various sizes in different places on the grid. You then take it in turns to guess the co-ordinates that your opponent’s ships are on. If you manage to hit the ship, then you have to keep going until you manage to sink the full ship. The game is over when a player manages to sink all of the other players ships. The mathematical processes that are involved in battleships include co-ordinates, rows, columns and positioning which are all very important mathematical processes. This highlights that teaching one of these concepts can be done through a fun and engaging way.

Although you do not need basic arithmetical skills for board games, you do need to have a secure knowledge of other basic mathematical concepts in order to play games such as Sudoku and Battleships successfully. One thing I have learned from this workshop is that the teaching of mathematics can be very supported through playing games. By reinforcing mathematical concepts this way, the children will become engaged and interested and as a result they will be encouraged to explore many mathematical concepts. As a teacher, this is something I will remember in the future as I feel as though it would be beneficial to both my practice and for my future class.

Felgenhauer, B. and Jarvis, F. (2005) Enumerating possible Sudoku grids [Online]. Available at: http://www.afjarvis.staff.shef.ac.uk/sudoku/sudoku.pdf (accessed: 27/11/2017

Maths in Taekwondo

Leave a reply

Taekwondo is something I have loved since a young age. Throughout my 17 years of doing this sport I have had to face many challenges however it wasn’t until our recent workshop that I started to think about the mathematics that are involved.

One of the most obvious concepts of mathematics is the scoring system that is used. In ITF taekwondo the scoring system is pretty straight forward. If you score a punch to anywhere in the body, then you gain one point. If you manage to land a kick to the body, then you gain two points and if you are lucky enough to score a head kick then you gain three points. As well as gaining points you can also receive warnings and lose points. If you hit the back of your opponent, then you get a warning. Stepping two feet out of the ring, falling down or using excessive contact can also warrant a warning. In taekwondo if you receive three warnings then you lose a point.

Here is a video explaining how it all works out.

(https://www.youtube.com/watch?v=uXrSEDmHonA)

During our workshop we were asked to develop a sport and change the rules to identify the mathematical concepts that would change the outcome. One of the main changes that we decided to change was the size of the ring. In ITF competitions, a standard ring is 9 metres by 9 metres however we decided to change this. As a group we decided to decrease the size of the ring in each round so that the fighters would have less chance to run around and avoid the fight.

We also decided that we should change the scoring system. In doing this, we changed the variables that points could be awarded. We decided to give one point for a punch to the body and two points for a punch to the head. This difference was introduced as we believed that a punch to the head was more difficult to score than a punch to the body. We then continued with a kick to the body worth three points and a kick to the head worth four points.

We also decided to change the times of the fights. We decided to make it a shorter time for each match as this would stop the running around with no contact. We believed that if we reduced the time for the fight then the fighters would give it their all for the full time in order to score as many points as possible. As a result, this would make it more exciting for spectators.

Another change that was decided was making the fights a match of doubles! This would mean that there would be 2 vs. 2 in the match which would completely change how the fighters would fight. We also spoke about the importance for other rules to be introduced to ensure that fighters did not just attack the same person for the duration of the fight. This idea is similar to the WWE tag-team wrestling matches.

This links to Liping Ma’s (2010) theory as she believes that maths cannot just be looked in one way and that it should be explored in as many ways as possible. This example of changing a sport can also be seen to represent multiple perspectives from Ma’s profound understanding of fundamental mathematics. We had to decided what rules we wanted to change and evaluate the impact of that on the outcome of the sport.

References

Bellos, Alex (2010) Alex’s Adventures in Numberland London: Bloomsbury

Ma, L (2010). Knowing and Teaching Elementary Mathematics. Oxon: Routledge. p120-125.

Tessellation

Leave a reply

Believe it or not, tessellation is something surrounding us in our daily lives. Look at the tiles in your bathroom, they will all be the same. Inside your kitchen? The tiles will show examples of tessellation as will the floor if it is wooden. Like chocolate? Who doesn’t?! Well that also shows tessellation as well as the skin on a pineapple. Like playing football? Well that ball is an example of tessellations using hexagons and pentagons.

Tessellation is the arrangement of one or more identical shapes that fit together perfectly to create a pattern. The most important thing about these shapes is that there should be no spaces or gaps within the pattern and that they are identical. By being identical I mean that all the shapes should be the same and the same size. When all of the shapes are the exact same then a tessellation occurs.

There are two different types of shapes that can occur within a tessellation, regular and irregular. The regular shapes include squares, hexagons and equilateral triangles whereas other triangles and quadrilaterals are irregular shapes. The difference between both of these is that with irregular shapes you have to rotate them in order to make them fit together and this is not necessary for regular shapes. All of these shapes are congruent which means that they are all the same size and even if you were to rotate a shape then it would still be the same. For example, if you rotate a circle then it is still a circle making it congruent. Regular shapes can create a tessellation as when all of the vertices touch one another then it all adds up to the sum of three hundred and sixty degrees.

Tessellations can be seen within the Islamic religion. The most common shapes that are used for tessellations within this religion is an equilateral triangle, a square and a hexagon. A star is also often used in the Islam religion and can differ between a 6, 8, 10 or 12 point star. A triangle is used a simple regular shape that represents harmony and a hum consciousness. The square is used as it highlights the four corners of the Earth while the hexagon that is used represents heaven.

Tessellations also relate to Liping Ma’s beliefs on profound understanding of fundamental mathematics. The basic idea within tessellations is the shapes that are used and how the fit with one another as well as the reasons why. This then leads on to longitudinal coherence as this basic idea can then lead to using this knowledge in order to explain more complicated concepts of area.

Profound Understanding of Fundamental Mathematics

Leave a reply

When I was first asked to describe what profound understanding of fundamental mathematics (PUFM) meant, the panic and fear immediately set in. To me this was something that seemed really complicated and confusing however upon further research and reading I have discovered this is not the case.

Liping Ma believes that there are four different properties in both teaching and learning which highlight a teacher’s profound understanding of fundamental mathematics that can be displayed within the classroom. These four properties include interconnectedness, multiple perspectives, basic ideas and longitudinal coherence. Therefore, Ma means that if a teacher can show these four properties successfully then they have a profound understanding of fundamental mathematics.

Interconnectedness is the idea that mathematic topics depend on one another. Ma (2010) describes a teacher with PUFM has making a great effort to show the connections between different mathematical concepts and procedures. She believes that when this is applied within a classroom then the pupil’s learning will not become fragmented and instead of being separate individual lessons, it will become one unified body of knowledge.

Multiple perspectives can be described as the ability to approach mathematical problems in many ways. This can be highlighted within maths as there are many different ways to reach the same answer and all of those different ways can be correct. Liping Ma (2010) says that teachers who have achieved PUFM are able to appreciate different ideas and approaches to a problem, taking into account the advantages and disadvantages. Also on top of this, teachers within a classroom should be able to explain the different mathematical concepts to a problem. By doing this, the teacher allows their pupils to develop a flexible understanding of mathematics and how it works.

The basic ideas within mathematics refer to the basic principles such as place value and ordering. Ma (2010) states that those with PUFM will show an awareness for these basic principles and appreciate their importance. These teachers will often revisit and reinforce these basic ideas and principles. This then means that pupils are not only encouraged to approach problems, but they are guided to carry out proper mathematical activity.

Longitudinal coherence can be explained as the way that one basic idea can build on another idea. Liping Ma (2010) believes that in order for a teacher to achieve PUFM then they should have a holistic view of the curriculum. These teachers are not just limited to the knowledge required for their stage as they have an understanding of the whole curriculum. Within a classroom, a teacher with PUFM is ready to take every opportunity to review crucial concepts and ideas that the pupils have covered previously. Longitudinal coherence can also be displayed within a classroom as the teacher will know what mathematical concepts that the class is going to cover in the future. They will prepare the pupils effectively by laying the proper foundations ahead of time.

These four properties are crucial to my understanding of mathematics and how to teach the subject. When I have my own class one day I will ensure I am a teacher that shows connectedness, highlights multiple approaches to problems, revisits and reinforces basic ideas and lays the proper foundations for future teaching.

Ma, L (2010). Knowing and Teaching Elementary Mathematics. Oxon: Routledge. p120-125.

Why teaching?

2 Replies

Why teaching?

Ever since I decided I wanted to become a teacher this is a question that I am often asked. I first discovered my love for teaching when I began helping out at my local taekwondo club. It was at this stage that I knew there was no better feeling than knowing you played a part in helping a young individual achieve one of their own personal goals. Though I was only eight years old this opportunity sparked my passion and determination to become a primary school teacher.

One of my main motivations for becoming a primary teacher is the idea that I can make a positive difference in a young persons life. This is personally a big thing for me as I always want people to achieve their own goals and be the best they can be. While on placement as part of my HNC course last year, I realised the topics I was teaching were the foundations of each child’s learning and this would equip them with the skills needed for future life. I can always remember coming home from placement each day feeling proud knowing I had helped a young individual and made a difference.

Fast forward to this year and I am now a first year education student at university! Reflecting back I always believed this was a dream that was so far out of reach. I still cannot believe that I am finally living my dream and one step closer to becoming a teacher.