1.4 Prof. Commitment | Teacher Education Blog

In a recent discovering mathematics workshop, we explored the mathematics behind various different games and puzzles. Board games are always something I loved as a young child. I would spend many days with friends and family surrounding a board game and having fun.

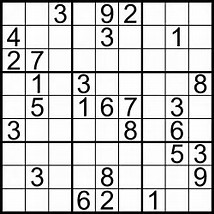
In this workshop we began looking at Sudoku. A standard game consists of a 9 x 9 grid with 81 cells however this can vary for more advanced and difficult Sudoku players. The aim of the game is to have the numbers 1-9 in a row, column and in a square. Normally when you start there will be some numbers that are already filled in and then you have to try and explore the different numbers that could fit. This is a game I have spent many plane rides or long car journeys playing however I have never really thought about the mathematical concepts behind this game. Some of the basic mathematical concepts in Sudoku is number, sequencing and problem solving. Throughout the workshop I learned that there are many different mathematical ways that people use in order to complete a Sudoku challenge. Upon further research I also found out that there 6670903752021072936960 different solutions to a standard 9 x 9 Sudoku grid (Felgenhauer & Jarvis, 2005).

Do you think you can complete a Sudoku? Give it a go!

We then went into groups to investigate different games and decide what mathematical processes were involved. My group decided to look into the game of battleships. In this game you place your ships of various sizes in different places on the grid. You then take it in turns to guess the co-ordinates that your opponent’s ships are on. If you manage to hit the ship, then you have to keep going until you manage to sink the full ship. The game is over when a player manages to sink all of the other players ships. The mathematical processes that are involved in battleships include co-ordinates, rows, columns and positioning which are all very important mathematical processes. This highlights that teaching one of these concepts can be done through a fun and engaging way.

Although you do not need basic arithmetical skills for board games, you do need to have a secure knowledge of other basic mathematical concepts in order to play games such as Sudoku and Battleships successfully. One thing I have learned from this workshop is that the teaching of mathematics can be very supported through playing games. By reinforcing mathematical concepts this way, the children will become engaged and interested and as a result they will be encouraged to explore many mathematical concepts. As a teacher, this is something I will remember in the future as I feel as though it would be beneficial to both my practice and for my future class.

Felgenhauer, B. and Jarvis, F. (2005) Enumerating possible Sudoku grids [Online]. Available at: http://www.afjarvis.staff.shef.ac.uk/sudoku/sudoku.pdf (accessed: 27/11/2017

Believe it or not, tessellation is something surrounding us in our daily lives. Look at the tiles in your bathroom, they will all be the same. Inside your kitchen? The tiles will show examples of tessellation as will the floor if it is wooden. Like chocolate? Who doesn’t?! Well that also shows tessellation as well as the skin on a pineapple. Like playing football? Well that ball is an example of tessellations using hexagons and pentagons.

Tessellation is the arrangement of one or more identical shapes that fit together perfectly to create a pattern. The most important thing about these shapes is that there should be no spaces or gaps within the pattern and that they are identical. By being identical I mean that all the shapes should be the same and the same size. When all of the shapes are the exact same then a tessellation occurs.

There are two different types of shapes that can occur within a tessellation, regular and irregular. The regular shapes include squares, hexagons and equilateral triangles whereas other triangles and quadrilaterals are irregular shapes. The difference between both of these is that with irregular shapes you have to rotate them in order to make them fit together and this is not necessary for regular shapes. All of these shapes are congruent which means that they are all the same size and even if you were to rotate a shape then it would still be the same. For example, if you rotate a circle then it is still a circle making it congruent. Regular shapes can create a tessellation as when all of the vertices touch one another then it all adds up to the sum of three hundred and sixty degrees.

Tessellations can be seen within the Islamic religion. The most common shapes that are used for tessellations within this religion is an equilateral triangle, a square and a hexagon. A star is also often used in the Islam religion and can differ between a 6, 8, 10 or 12 point star. A triangle is used a simple regular shape that represents harmony and a hum consciousness. The square is used as it highlights the four corners of the Earth while the hexagon that is used represents heaven.

Tessellations also relate to Liping Ma’s beliefs on profound understanding of fundamental mathematics. The basic idea within tessellations is the shapes that are used and how the fit with one another as well as the reasons why. This then leads on to longitudinal coherence as this basic idea can then lead to using this knowledge in order to explain more complicated concepts of area.