








I love a good night out to the Casino; throwing money i don’t have, on a risky bet with nothing but high hopes of a win. Its an amazing feeling walking away from any game in the casino with a profit; Roulette however, is especially dramatic to come away with a win.
away with a win.
This is due to the higher risk taking within the game of Roulette than compared to blackjack or poker for example. There are several options while betting on a roulette table; Red or black/Even or Odd holds a 1/2 chance of a win, betting in one of the ’12th’ brackets holds a 12/37 chance and betting on any singular number hold a 1/37 chance of winning. The lower the probability of the win, the higher amount of money you could win back.
Therefore looking at the mathematical sides of the game it is very difficult to walk away with a big win on a singular number. Watching Derren Browns documentary ‘How to take down the casino’ opens my eyes to other mathematical concepts within gambling. He studied the speed, distance and time of the wheel spinning in attempt to calculate the point that the ball would stop. Not only was the speed of the wheel important but also the speed of the ball needed to be mentally calculated within seconds. This seems virtually impossible to be done by any human being. He spends years doing mini practises in such like scenarios, such as, estimating the speed that a car is driving within a certain distance. I find this an incredible skill, as he gets them correct by testing his answer against a speed gun.
With all his practise, he finally puts the mathematics theory to the test by betting £5000 on a singular number in roulette. Looking back at the statistics, this holds a one in 37 chance of winning at random. As he used calculates the mathematics while the wheel is spinning, he has a split second to place his bet once the ball is spun. Unfortunately, he was one place off. However this still shows that the mathematics behind it provides a more logical bet than selecting a number at random. Knowing the theory to calculate is also important in itself, even if humans don’t always get it right. It is with this logic, that they have then been able to go on to invent machines that can calculate the answer every time. As we’ve already seen it used in speed detectors, this is an essential part of equipment used in society today.
Therefore, although using mathematical concepts while gambling increases your chances of winning it still cannot guarantee a win but worth a try? This discovery highlights that mathematics surrounds us, even in our social life, we are constantly thinking about the probability of something happening or what the chances that we have to win.
Science and maths are beginning to appear more and more within sport games.
Especially, the worlds most popular sport, football. Football is such a competitive sport and thousands of people rely on this as a career. The money factor of football increases the significant value and seriousness of the sport. Going from a range of manager’s jobs, professionals wages to the general public’s bets, millions of people rely of a games outcome. To heightening the probability of a win for a team, a manager would have to consider which players are better for certain positions in a team. To ensure which players are best for a particular team, they need to consider their strengths and weaknesses and how they could fit in the team persona. Using statistics drawn from previous matches played, we are able to see each players successful pass rate, speed/distance ran and shot conversion (and much, much more), therefore managers are able to identify the areas that need improved within their team and which players they can buy to help. Questions such as, how many corners were taken by each team? how many fouls have been given to each player? how many assists have players set up? and even a debate of who is the best player in the world? can all be settled or at least narrowed to a handful of players.
Statistics can also benefit football teams as they can provide a deeper understanding and evaluation of tactics and team performances of opposing teams. Using the data, diagrams, graphs and maps can be drawn up of how players use the pitch, as shown below.

This diagram shows the passes played by Manchester United across the pitch in one game. Each line demonstrates the direction of the pass and the length presents how short or long the shots were. The colours all how significant meaning also; Black shows that a pass is relatively common whereas white highlights less frequent passes and brown shows somewhere in between.
This data establishes that Manchester United use the wings of the pitch more often than straight through middle. This is a tactic that the opponent team would want to consider and be aware of to try defeat them.

We can use these maps to compare the different tactics used by each team. The second map on the left displays Arsenals passing during a game. I find this a good contrast to Manchester United’s passing as we can clearly see that Arsenal use shorter, more precise passing and tend to focus passes in front of the box to create chances. This is just one of the ways that mathematics can be visualised to benefit the football industry.
Match of the Day is on sky sports every Sunday evaluating and analysing all these statistics for every game in the Premier League. As the professionals critical analyse and discuss each shot, pass and tackle made, this knowledge is then pass on to the wider society. With extra insight into players ability and team tactics, the gamblers in the public, can use this information to place logical bets on predicting pretty much any move of the game. A common bet could be prediction of which players receive a foul. For example, Sergio Aguero is known for being a bit more aggressive than other players, therefore, when he is playing, betters take this likelihood into account in order to win a profit.
As well as statistics supporting predictions and increasing performance of football, the physics of the sport is also a crucially important mathematical factor. I have seen many goals disallowed as the balls hits off the cross bar and spins bouncing outside the goal line. An example of this is back in the 2010 World Cup game between England and Germany, where Frank Lampard’s shot struck against the cross bar and bounced half a metre behind the line. This raised question as to why the ball bounce outside the goal again rather than continuing into the back of the net? The University of Bath looked into the complex process of physics of why the ball spins out of the net. They studied the angle and speed at which the ball hits the crossbar and how much of a spin it put onto the ball. Experiments showed that the closer the ball was to the goal line while bouncing, the more spin it had, resulting in the ball bouncing the opposed way than expected. This is because of the horizontal velocity of the ball being reversed. This is shown in the diagram below- red line demonstrating the ball bouncing closest to the line ending up bouncing back out the goal.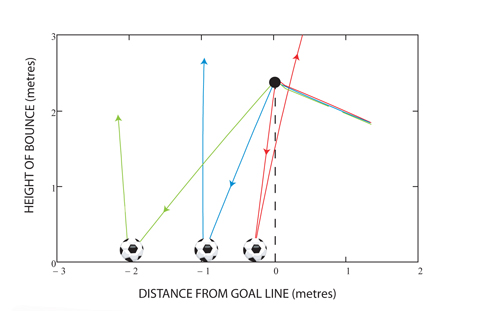
The University’s experiment also found that the surface of the ground made a difference to the spin of the ball.To read in more depth on the mathematical process of the physics of the ball- https://plus.maths.org/content/when-goal-not-goal
This type of mathematics is seen in many other sports such as basketball, netball, baseball, cricket etc. This reiterates the great Importance that mathematics makes in the industry of sport and how it impacts on the wider society. After reading into the concepts of maths within football, I have became more aware of why a manager had played a certain player in a certain position or why the ball has spun out of the net and rather than just relying on technology to figure these statistics out, it all comes down to the mathematics behind it. I also feels that I would be able to use my knowledge of statistics to teach maths to children that find football interesting to engage them and demonstrate that mathematics is EVERYWHERE!
References
https://www.fourfourtwo.com/features/soccermatics-how-maths-will-change-your-understanding-football
http://jwilson.coe.uga.edu/EMAT6680/Huffman/Mathematics%20in%20Sports/MathematicsSports.html
Far too often I hear people associating maths as numbers and languages with words and speaking. As I read into discovering maths more, I realise that this is not the case and it can have an impact on how children learn.
Liping Ma’s discovery has taught to be cautious about the words i use while teaching children maths, for example, expressing to decompose a fraction rather than borrow. this made sense to me as it provides a more visual image for the children to break down the fraction rather than steal a tens value. I then looked into other ways that maths can be used as a universal language. When children see the mathematical symbols (+,-,X,=) it is seen as an unfamiliar language that is not as straight forward as the spoken language, similarly to the way people who do not understand Chinese view their symbols.
“What seems to happen with many children is that they develop a completely separate way of thinking about the math they do at school, because it fails to integrate with their accomplished informal ‘home’ mathematical language” (Atkinson, 1998, pg 18)
This video by Randy Palisoc illustrates that maths being taught as a language is a lot more comprehend-able for children.
I like the idea of mathematics becoming more human, as i must admit, I once considered maths as the classic myth that it is solely for the ‘clever’ people.
“If the maths its self is not presented in a way that is meaningful to children, if it fails to make ‘human sense’, and if unfamiliar language is used, problems most inevitably arrive.” (Atkinson, 1998, pg 17).
I believe that teachers shouldn’t be afraid to use more language in teaching maths because it makes it more real for children while learning. By referring to the 4 principles of mathematics (Interconnectedness, basic ideas, multiple perspectives and longitudinal coherence) we can show children just how common maths is.
As a teacher it is essential to demonstrate the [inter]connectedness within every topic in maths. By taken children’s prior knowledge and displaying how it can support other mathematical problems, ill deepen their understanding and will eventually independent-learning as they begin to make links themselves. For example, knowledge about fractions and angles would be necessary to recognise how to complete trigonometry efficiently.
Through teaching Multiple perspectives within a topic provides flexibility for the children’s learning. I was definitely one of those children that needed something explained to me over and over again before i understood it. Approaching a question with an open mind to several ways of solving it, creates a less ‘scary’ ideological that there is only one correct answer in maths.
Teachers must have a profound understanding of the basic ideas within maths in order to reinforce these to the students. Basic ideas of maths can become reoccurring as children progress through mathematics, these can also be sufficient links for the children to make to develop their learning.
Longitudinal coherence is this idea of building blocks in maths. using prior knowledge we can then begin to extend their knowledge onto more complex situations. For example, once children have got to grips with multiplication and division of whole numbers, teachers can then develop their learning further by introducing fractions.
By appreciating these approaches, teachers can make teaching maths more efficient for children to master maths and avoid the false phenomenon that maths is too difficult for them.
References
Atkinson, S. (1998). Mathematics with reason. London: Hodder & Stoughton.
Ma, L 2010, Knowing and Teaching Elementary Mathematics : Teachers’ Understanding of Fundamental Mathematics in China and the United States, Taylor and Francis, Abingdon, Oxon. Available from: ProQuest Ebook Central.
Horology is defined by the art or science of measuring time, such as watchmaking. Horology is a complex process which is full of mathematical processes in order to succeed in creating an accurate watch. Ilan Vardi describes mathematics as language with the use of equations and formulas however what distinguishes it from other subjects is the idea of philosophy. For example, the understanding and completion of any mathematics problems tends to be by discovering the order in things. Mathematicians and watchmakers share very similar interest;his job is to establish a sequence that tracks the measurement of time. the series of events that allows the clock to show the correct time and continue the constant measuring of time.
But what is time? I believe its important to emphasis to children the actual value of time. We all know that counting 60 seconds = 1 minute and 60 minutes = 1 hour. Similar to place value, this can be a very difficult process for children to first understand.
Dave Allen demonstrates how complication teaching time can be.
Giving children a background to why time is important (keep track of days, weeks, seasons etc.) would be a more efficient form of guiding their understanding. If they understand the importance of time keeping and why humans use the units we do, they would see the relevance of the subject rather than being told how to read a clock. Before discussing how we record time nowadays, we could consider teaching about sundials or Egyptian water clocks. By learning about other measurements of time can highlight how we can came to using the clock/watch today.
Egyptians waterclock were one of the first timekeeping devices that did’nt use the sun, in the 16th century BCE. It worked by recording the flow of water dripping at a constant rate from a bowl through the a small hole in the bottom. As the water levels went down and several markings in the container allowed them to know how much time has passed. i found it particularly interesting to discover that the Egyptians also used an instrument called merkhet, that followed the alignment of the stars in order for them to know what time of night it was. They identified 10 hours of night because of the 10 stars and then gave 1 hour for the sunset and sunrise, giving a total of 24 hours day and night. This is an interesting fact as to why we still use 24 hours today!


This finding again, highlights that maths is everywhere and has been for a very long time. This encounter of the origin of time has gave me a deeper understanding of why we record time today and how essential maths has been to creating the world and life that we live today.
Liping Ma has undergone research to compare the differences on how mathematics is taught in China and the USA. Her findings were fascinating; even though US students go through more education to become a teacher than those in China, the Chinese teachers have a deeper understanding of mathematics and therefore are able to teach more efficiently. She found that American teachers taught more in a procedural way rather than using the logic of mathematics.
“About 10% of those Chinese teachers, despite their lack of formal education, display a depth of understanding which is extraordinarily rare in the United States.” (Liping Ma, 2010)
I was edger to find out more about Liping Ma’s discover; How do the chinese teachers teach more efficiently? and what can I learn from this for the future?
In Liping Ma’s book ‘Knowing and Teaching Elementary Mathematics’ she explains her theory and suggests how the Chinese teachers understanding how maths contributes to the students success. This is an important theory that i would consider while teaching children mathematics.
and suggests how the Chinese teachers understanding how maths contributes to the students success. This is an important theory that i would consider while teaching children mathematics.
so why is it that Asian children consistently outperform American students? there are many factors that researchers have found that contribute to this “learning gap”;
Researcher Deborah Ball identified teachers knowledge and understanding of mathematics should be connecting ideas of and about the subject. The concept by the knowledge of mathematics meant; “comprehension of particular topics, procedures, and concepts, and the relationships among these topics, procedures, and concepts.” (Liping Ma, 2010). therefore, understanding all these things and making it clear to the students will assist them reaching success. The meaning behind the knowledge about mathematics is aiming at the comprehension of the nature and discourse of mathematics. Additionally teachers consistently thinking about the ‘substantive knowledge’; correctness, meaning and connectedness. Mathematics should always be open to more than one way solutions. Students who can solve a problem with a variety of methods will be able to achieve higher, as the skills can be applied to similar situations. I believe this is important for myself and teachers to consider while teaching because if we notice a child struggling to grasp a process, it may be beneficial to teach another method that they could use. Hopefully seeing another method will be the situation clearer for the child rather than becoming frustrated.
As Liping ma was researching she drew on how teachers taught; subtraction, multiplication, division by fractions and perimeter. I mainly looked into subtraction and found her way of teaching a lot more enlightening. She studied the American the method of borrowing or exchanging in subtraction, so for example, discussing that when subtracting 21-9 that they had to borrow unites from the tens column. she realised that teacher were expecting students to know, based on their knowledge, from a very procedural method of teaching.
Chinese teachers mainly use a regrouping method of subtraction and in contrast with US teachers, 35% of them demonstrate multiple ways to carry out regrouping. Liping Ma states that teachers address the standard algorithm as well as discussing other ways to solve a problem. The main method of regrouping is by decomposing a unit of higher value, so breaking down the hundreds, tens and units number. for example using 21 again, Chinese teachers would decompose the number rather than suggesting to borrow. This highlights that the language a teacher uses is crucial to help students understanding. Using ‘borrowing’ can confuse children as it acts as a metaphor whereas decomposing highlights that the higher digit can be broken down. Linking what happens when the children done addition is also important to help them understand how 10’s are formed and taken away.
An example of the regrouping by a Chinese teacher from Liping Ma’s (2010) book- “How come there are not enough ones in 53 to subtract 6? Fifty-three is obviously bigger than 6. Where are the ones in 53? Students will say that the other ones in 53 have been composed into tens. Then I will ask them what can we do to get enough ones to subtract 7. I expect that they will come up with the idea of decomposing a 10. Otherwise, I will propose it. (Tr. P.)”
An example of borrowing from An American teacher- “Where there is a number like 21−9, they would need to know that you cannot subtract 9 from 1, then in turn, you have to borrow a 10 from the tens space, and when you borrow that 1, it equals 10, you cross out the 2 that you had, you turn it into a 10, you now have 11−9, you do that subtraction problem then you have the 1 left and you bring it down.”
Students that understand why higher value units need decomposed is more efficient than borrowing as they can also apply this knowledge when working with three digit equations. Once they’ve learned the facts and the procedure they an apply this to any situation they are in.
What I take away from Liping Ma and Deborah Balls’ theory is that teachers must be able to anticipate children’s response in order to encourage their way of working and not to simply restrict them to one method. Displaying multiple methods of solving a problem is essential as it promotes more independent learning and also a better variety as each child learns differently. I will also be more cautious of the language i use in the classroom to ensure I provide the best learning situation and avoid confusing the children.
References
Ma, L 2010, Knowing and Teaching Elementary Mathematics : Teachers’ Understanding of Fundamental Mathematics in China and the United States, Taylor and Francis, Abingdon, Oxon. Available from: ProQuest Ebook Central. [4 October 2017].
Cuarezma, A. (2013). Q & A with Liping Ma. The New York Times. [online] Available at: http://www.nytimes.com/2013/12/18/opinion/q-a-with-liping-ma.html [Accessed 4 Oct. 2017].
An Abacus is one of the first counting devices invented and I was intrigued why it was used?
It is a simple wooden/ plastic framed tools with beads used to show a visual representative of place value and assist addition, subtraction, multiplication and division. It can be used as a calculator by sliding the beads along the rods (which is a lot funnier than typing on a calculator!). The abacus has been around for around 2500 years and as primarily used in countries such as China, Korea, Japan etc but it’s now recognised by most of the world.
The abacus tool is not used as often in schools anymore as devices change and evolve however, an assistant psychology professor at the University of California in Riverside, Aaron Seitz, (South China Morning Post, 2011) states that children should not just be writing to learn maths but should be using other senses to consolidate their learning.
“Maths is not strictly verbal, tactile or a language; it is a kind of an abstract representation and so if that abstract representation is built upon information from multiple sensory modes, it is going to be more developed and more effective than coming from a single sense.” (South China Morning Post, 2011)
The experience that children gain with using the abacus is more successful as they can use physical touch, sound of the beads and visually looking at them as more efficient tool to grasp rather than simply writing down a sum on paper.
The following youtube video demonstrate how a child uses the basic abacus to assist with his maths.
(Addition and Subtraction by Abacus, 2016)
The abacus is especially useful in early years so the children can understand the concept of the number holding a quantity by the visual representation of the beads. I believe the abacus is still important to use today as it is one of the easiest and more fun ways for children to understand addition and subtraction.
Although abacus is not used as often anymore, i believe the reason behind the abacus is important to ensure the best learning opportunities for young children. Many other ways teachers can use maths in a physical form such as getting the children to count (add or subtract) money, sweeties or each other. After, researching about the abacus, I will take into consideration while teaching the basics of addition and subtraction that if need be, i know it is an effective tool that i can implement.
References
South China Morning Post (2011). Ancient abacus still has a place. [online] Available at: http://www.scmp.com/article/971772/ancient-abacus-still-has-place [Accessed 10 Oct. 2017].
Addition and Subtraction by Abacus. (2016).Mostofa Saadi.
Maths is much more than boring equations full of numbers!
Mathematics is bursting with shapes, patterns, science, history, art, the list is goes on. so why do we just assume that maths is challenging sums?
Islamic art is a perfect example of how maths links with other subjects. As Eddie explained how angles and shapes fall into this art piece, i was enjoying the maths that i once hated! Everyone, no matter how young or old, are more engaged when they can physically make, play or colour-in. I believe this is a vital fact to remember when teaching a class a subject like maths, that can go one or two ways; enjoyable or fearful.
Geometry- if uni students found it enjoyable, primary kids will love it!


….MATHS IS EVERYWHERE!
I could honestly say i tried very hard to avoid maths as soon as I walked out of school two years ago. But, stepping back into a module of discovering maths, its brought my realisation that i physically cannot escape the “terrifying fears” that comes with mathematics. No, maths isn’t really that bad. In fact we mainly use maths by doing what we love in our everyday life, playing sports for example, or betting. During our school years we are taught about the simple arithmetic skills all the way up to complex processes of algebra. We may not think we use the complicated formulas in algebra but there are many occasion that we would use the problem solving skills without realising.
History of Mathematics…
“The history of mathematics is nearly as old as humanity itself. Since antiquity, mathematics has been fundamental to advances in science, engineering, and philosophy. It has evolved from simple counting, measurement and calculation, and the systematic study of the shapes and motions of physical objects, through the application of abstraction, imagination and logic, to the broad, complex and often abstract discipline we know today” (Luke Maston, 2010). The simplest of maths has grown over the years to create the complex world we live in today. In the beginnings of agriculture, mathematics helped form civilisation as maths was used to measure acres of land. Without it, it would not be clear of whose land is whose, which is crucially for food source back in time.
Mathematics can range from as simple as setting an alarm clock in the morning to as complex as coding a program for electric devices for example. The possibilities of mathematics is endless and I truly believe we should strive to encourage mathematics in all subjects that we teach and not to fall into the trap of fear. Continuously expressing the relevance of maths is crucial while teaching the young minds of children as they are the future and will go on to use maths as an essential tool.
Luke Maston. (2010). The Story of Mathematics – A History of Mathematical Thought from Ancient Times to the Modern Day. [online] Available at: http://www.storyofmathematics.com/ [Accessed 25 Sep. 2017].
Glow Blogs uses cookies to enhance your experience on our service. By using this service or closing this message you consent to our use of those cookies. Please read our Cookie Policy.