Section 2 – Newton’s Laws
(refer to examples in Summary Sheets Part 1)
Force is a vector
Force is a vector quantity. The direction that a force acts in will dictate the effect that it has.
Balanced Forces
Two forces acting in opposite directions are said to be balanced. The effect is equivalent to no force acting on the object at all.
Newton’s First Law
“An object will remain at rest or move at a constant velocity in a straight line unless acted on by an unbalanced force”.
This means that if the forces acting on an object are balanced, then the object will remain stationary if it was already stationary. For a moving object, if the forces acting on it are balanced, then it will continue to move in a straight line at a constant velocity.
balanced forces ↔ Object at rest OR object moving at a constant velocity in a straight line
Newton’s Second Law
If an overall resultant (or unbalanced) force is applied to an object, then the object will accelerate in the direction of the unbalanced force.
- The greater the resultant force, the greater the acceleration.
- The smaller the mass, the greater the acceleration.
These two relationships are combined to give
This equation shows that a force of 1 N is the force needed to accelerate a mass of 1 kg at a
rate of 1 m/s2
Free Body Diagrams and Newton’s Second Law
“Free body diagrams” are used to analyse the forces acting on an object. The names of the forces are labelled on the diagram. (It is also useful to mark the sizes of the forces on the diagram).
This enables us to calculate the resultant force, and then apply Fun=ma.
Forces at Right Angles
The resultant force arising from two forces acting at right angles can be found by
(a) Drawing the force vectors “nose-to-tail”
(b) Calculating the magnitude using Pythagoras
(c) Calculate the direction using trigonometry (SOH-CAH-TOA)
(Alternatively, you could draw the vectors “nose-to-tail” as a scale diagram. Then find the magnitude using a ruler and your chosen scale, and the direction using a protractor).
Example
Two forces act on an object at right angles to each other as shown.
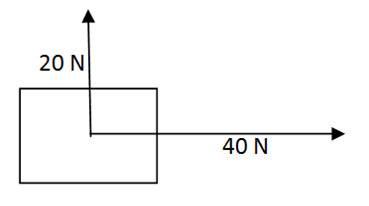
Calculate
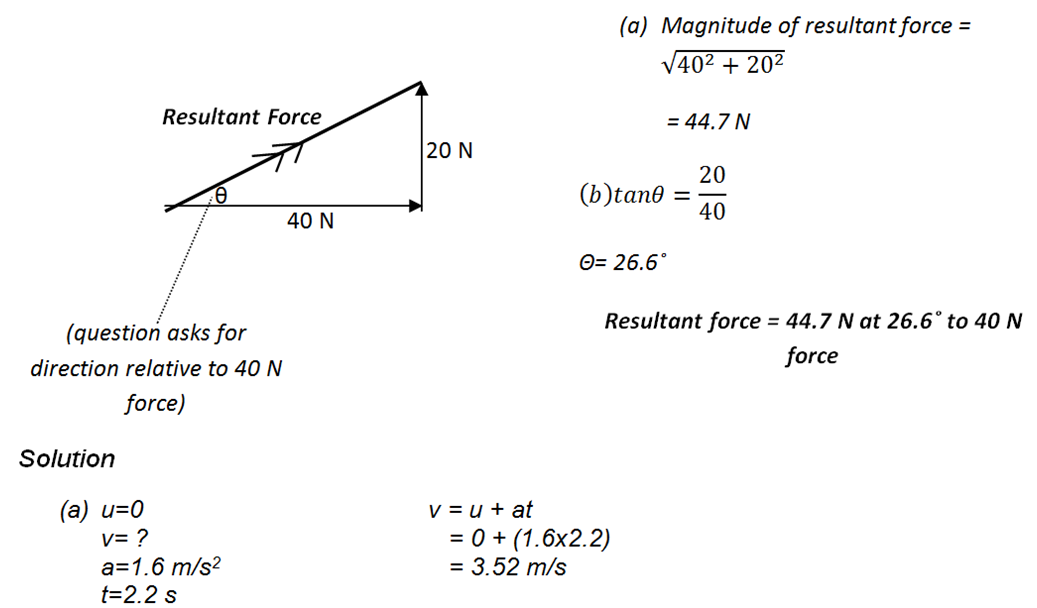
(a) The magnitude of the resultant force
(b) The direction of the resultant force, relative to the 40 N force.
Solution
(arrange vectors “nose-to-tail” and draw resultant from tail of first to nose of last)
Newton’s Third Law
“For every action, there is an equal and opposite reaction”.
Newton noticed that forces occur in pairs. He called one force the action and the other the reaction. These two forces are always equal in size, but opposite in direction. They do not both act on the same object.
If an object A exerts a force (the action) on object B, then object B will exert an equal, but opposite force (the reaction) on object A.
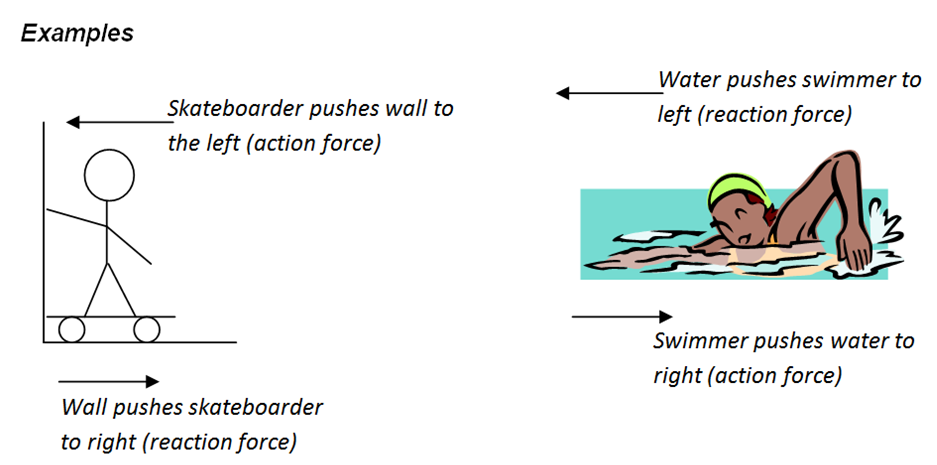
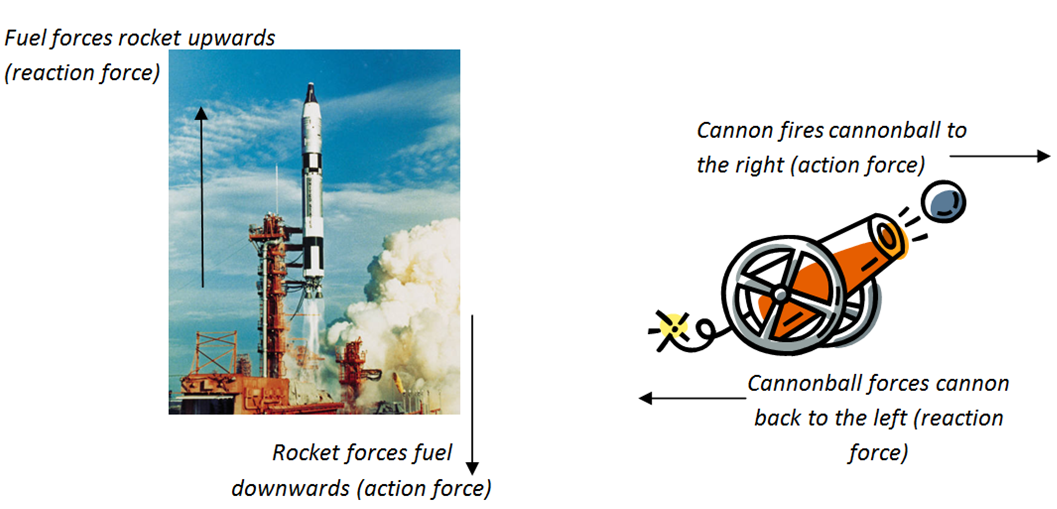
These action and reaction forces are also known as Newton Pairs.