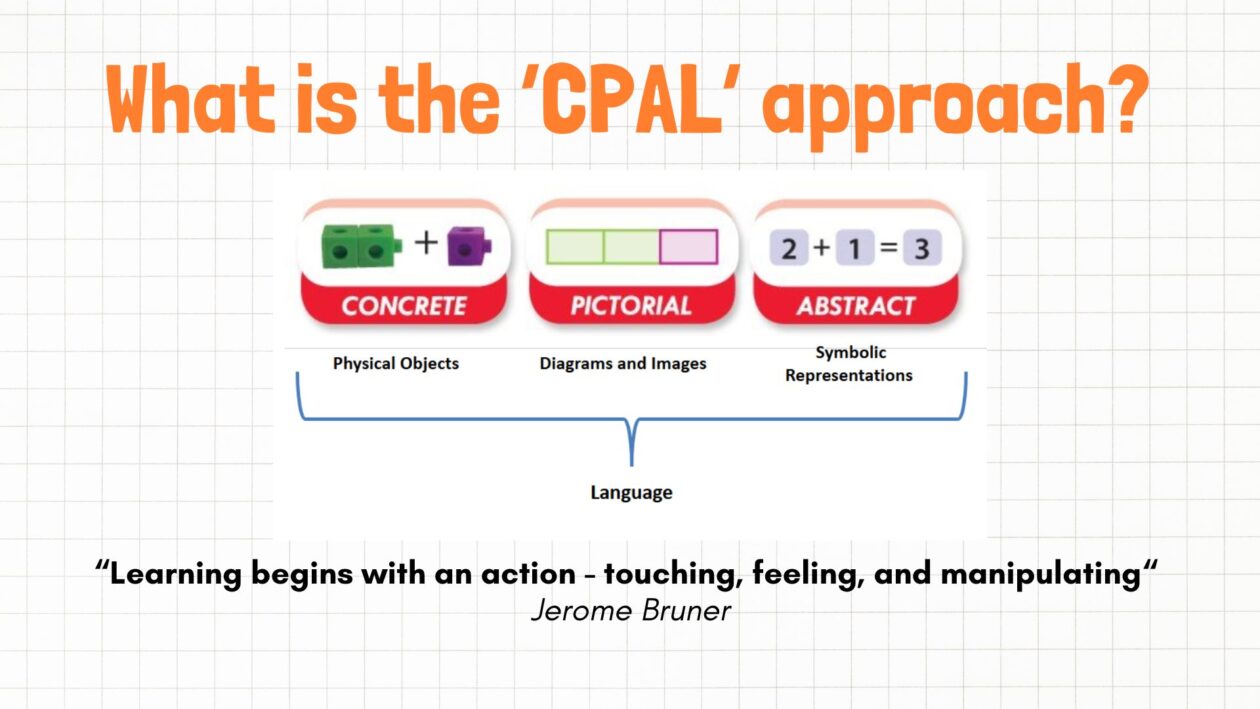
What is CPAL?
The Concrete Pictorial Abstract (CPA) approach is a pedagogy that uses physical materials and visual aids to build a child’s understanding of abstract maths. Originally popularised as ‘CPA’, by American psychologist Jerome Bruner as part of his scaffolding theory, it is a cornerstone of teaching for deep conceptual understanding. Bridging the gap between the real world and abstract symbols, the CPA approach is based on the premise that “children must hold maths in their hands, before they can hold it in their heads.”
In many Scottish classrooms, we are moving away from pages of ‘sums’ and rote memorisation of procedures, toward a model that ensures learners truly “see” and understand the maths. The approach is built across three main stages, with an important fourth element which brings vital cohesion across all stages: Language.
- Concrete: Learners use physical manipulatives (e.g., Unifix cubes, Numicon, Dienes blocks, or even everyday items like straws) to model a problem. This makes the abstract nature of maths tangible. For further guidance on how to use specific concrete manipulatives, head to our ‘Tools’ page. For access to a range of online manipulatives, ideal for teacher modelling and demonstration, visit Manipulatives – MathsBot.com or Math Apps | The Math Learning Center.
- Pictorial: Once comfortable with physical objects, learners move to visual representations. This might involve drawing “dots,” bar models, or sketches of the manipulatives they just used. This stage is the vital “bridge” to mental visualisation. For further examples and guidance on how to use specific pictorial models, head to our ‘Tools’ page.
- Abstract: Only when the underlying concept is secure do learners move to abstract symbols and formal notation (e.g., 15 + 7 = 22).
- Language: Language is the ‘glue’ that brings each stage together and encourages children to make connections between different representations of the maths. Throughout every stage, consistent use of mathematical language and purposeful questioning, allows learners to articulate their thinking and solidify their understanding.
Why are Teachers Making the Switch?
The CPAL approach tackles the “maths anxiety” and “rote mimicry” often found in traditional teaching of maths. Here is how it redefines the mathematical experience:
- Conceptual Depth over Rote Memorisation: Instead of memorising a “trick” (like “carrying the one”), learners use Dienes blocks to physically exchange ten ones for a ten-rod. This builds a “why” behind the “how.”
- Visualisation Skills: By moving through the Pictorial stage, learners develop the ability to create “mental images” of numbers in their heads. This is a hallmark of successful mathematicians at any age.
- Accessible Differentiation: CPAL allows all learners to access the same high-quality curriculum. While some might be working with counters and others drawing bar models, they are all exploring the same mathematical concept.
- Evidence-Based Success: Heavily influenced by the success of “Singapore Maths,” CPAL is now a key part of the National Council for Excellence in the Teaching of Mathematics (NCETM) and aligns perfectly with the Curriculum for Excellence (CfE) principles of depth and challenge.
Who Benefits from the Approach and Why?
While CPAL is a win for the entire learning community, specific groups see unique benefits:
- Reluctant or Lower-Confidence Learners: These learners often struggle with the “invisibility” of abstract numbers. Concrete resources provide a safety net, giving them something physical to manipulate and “prove” their answers.
- High-Achieving Learners: These learners are challenged to move beyond “getting the right answer” quickly. They are pushed to prove andjustify their thinking using a pictorial model or to explain the concrete process, which prevents “procedural superficiality.” They are encouraged to use ‘multiple representations’ to demonstrate the depth of their understanding.
- Teachers: The role of the teacher shifts from a lecturer to a facilitator. By observing how a child manipulates resources or draws a model, you gain an immediate “window” into their misconceptions that a simple written answer wouldn’t reveal.
- The Classroom Community: CPAL encourages discussion. When learners have a physical or visual model in front of them, they have a shared reference point to explain their strategies to peers, fostering a collaborative “Maths Talk” culture.
Common Issues CPAL Helps Address
CPAL was designed specifically to solve the flaws in the “abstract-first” teaching model:
- Learner Passivity (“Mimicry”): In many lessons, learners copy a method without understanding it. CPAL forces them to build the logic from the ground up.
- The “I’m Not a Maths Person” Myth: By making maths “real” and visible, CPAL dismantles the idea that maths is a secret code only some people can crack.
- The “Gap” in Upper Primary: Often, learners who seem “good at maths” in P3 struggle by P6/P7 because they never truly understood place value. CPAL ensures the foundations are rock-solid before moving to complex formal algorithms.
- Difficulty with Word Problems: Many children can do a calculation but can’t apply it within a context. The Pictorial (Bar Modelling) stage is specifically designed to help learners “decode” word problems and see the structure of the maths involved.
The Concrete Pictorial Abstract approach isn’t just a “support” for those struggling; it is a fundamental way of thinking and learning that ensures every learner in your classroom can become a confident, creative and successful mathematician.