What is computational thinking?
Computational thinking allows us to do this.
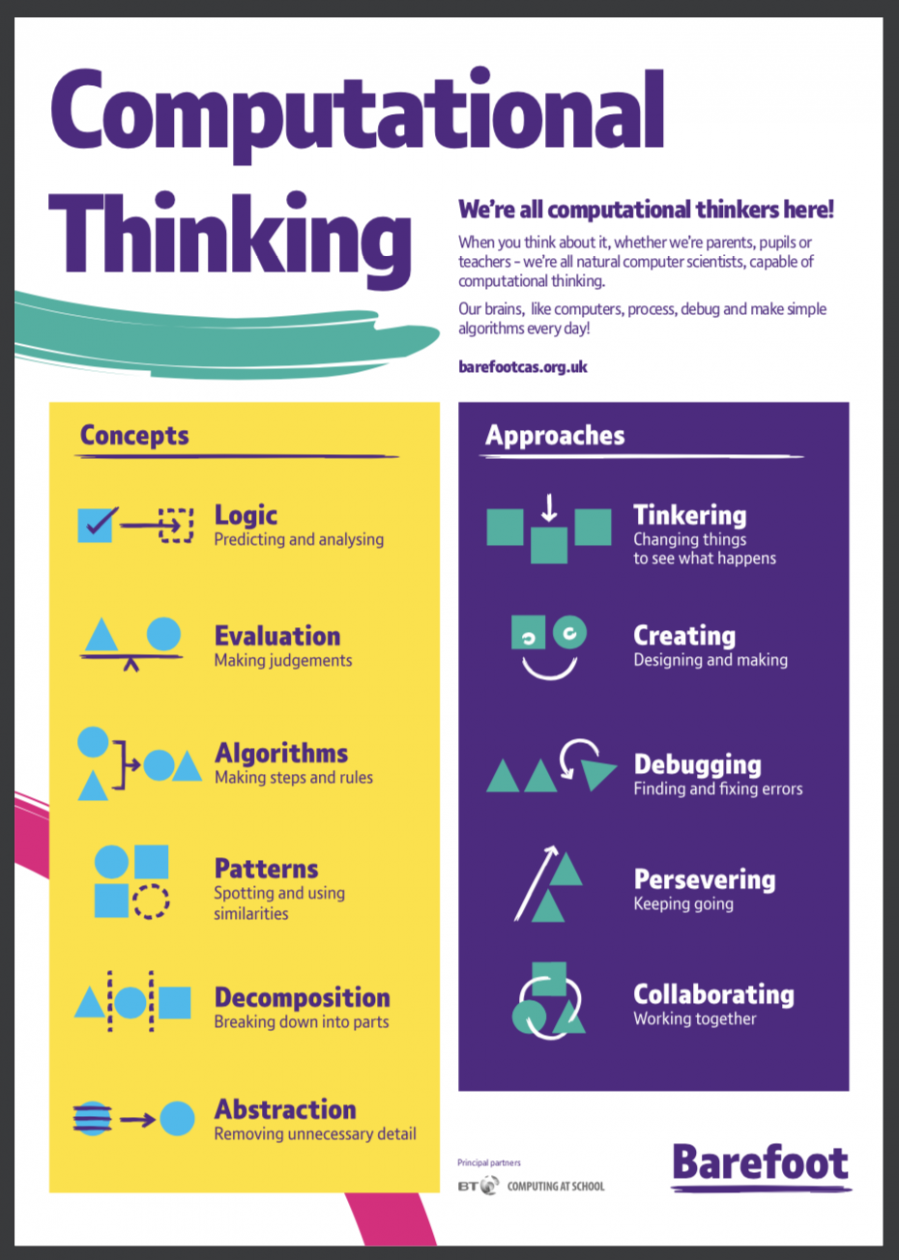
The four cornerstones of computational thinking
There are four key techniques (cornerstones) to computational thinking:
- decomposition – breaking down a complex problem or system into smaller, more manageable parts
- pattern recognition – looking for similarities among and within problems
- abstraction – focusing on the important information only, ignoring irrelevant detail
- algorithms – developing a step-by-step solution to the problem, or the rules to follow to solve the problem
Each cornerstone is as important as the others. They are like legs on a table – if one leg is missing, the table will probably collapse. Correctly applying all four techniques will help when programming a computer. (More information HERE )
Barefoot Computing is a great FREE resource , and the resources are mapped to Curriculum for Excellence and the current Experience and Outcomes. The materials provide learning opportunities to support aspects of the broad general education Computing Science curriculum within the Technologies whilst also providing interdisciplinary experiences across the curriculum.
Barefoot add Logic and Evaluation as key concepts, but you will see the Computational Thinking concepts and approaches could be used anywhere in the curriculum.